数学思想在几何中的渗透

周海莲

在初中几何计算里，求三角形的边、角、周长、多边形的边数等，都渗透着不少数学思想.

一、化归思想

将所要研究和解决的问题能转化为已经学过的问题来处理的数学思想称为化归思想，它是一种研究和解决数学问题的基本思想，如在求多边形的内角和基本思路是将多边形分割成三角形的内角和来求多边形的内角和.

下面通过五边形的内角和演绎出推导多边形的内角和的方法.

【例1】 如图，小颖和小芳分别利用图①、②所示的两种不同方法求出五边的内角和，请你在图③中用另一种方法求五边形的内角和，并写出求解过程.

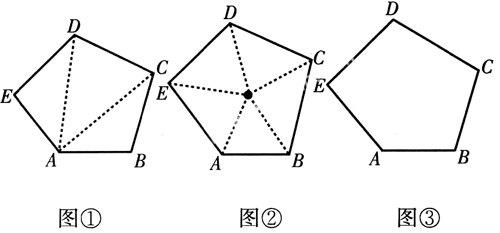
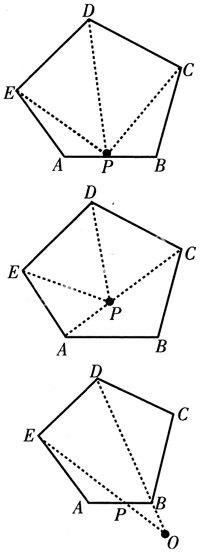
解析：解法一：在一边(AB)上取一点P，连接PC、PD、PE，它们将五边形分成4个三角形，五边形的内角和等于4个三角形的内角和减去一个顶点在AB边上组成的平角，即4×180°-180°=540°.

解法二：连接AC，在AC上任取一点P，连接PD、PE.它们将五边形分成4个三角形，五边形的内角和等于4个三角形的内角和减去一个三个顶点在AC上组成的平角.即4×180°-180°=540°.

解法三：在AB上任取一点P，连接EP并延长对角线DB的延长线于点O，它们将五边形分成3个三角形，五边形的内角和等于3个三角形的内角和减去多加的∠O和∠APE，又加上少加的∠DBP.而∠DBP恰好是△OBP的外角，所以，而∠BPO=∠APE(对顶角相等)所以∠DBP=∠O+∠APE，所以五边形的内角和等于3个三角形内角和，即

3×180°=540°.

二、分类思想

在三角形三边之间的关系中，已知等腰三角形的两边求周长或已知周长求另外两边，渗透分类讨论思想.

【例2】 已知等腰三角形的一边长为7，另一边长为3，求等腰三角形的周长.

分析：边长为7的边可以为腰，也可以为底边，故需要分类讨论.

解析：边长为7的边可以为腰，也可以为底边，

若边长为7的边为腰，边长为3的边为底边三角形的周长为：7×2+3=13.

若边长为7的边为底边，边长为3的边为腰，而3+3=6<7．故腰为3，底的等腰三角形不存在，所以三角形的周长为13．

三、方程思想

在几何的计算中，求三角形的角，多边形的边数，往往通过已知量和未知量的联系建立起方程，通过解方程求出三角形未知的角和多边形的边数.

【例3】 已知△ABC的三个内角的度数之比为∠A∶∠B∶∠C=1∶2∶7，试判断这个三角形是什么三角形?

分析：已知条件中给出的是角之间的关系，并没有具体给出角的度数，可借助方程来求角，由于只判断三角形的形状，不需要求出每个角的大小，只要求出最大的角就可以判断三角形的形状了.

解析：设∠A=x，∠B=2x，∠C=7x.根据三角形内角和定理，得x+2x+7x=180°,x=18°.

∠C=7x=7×18°=126°.

所以△ABC是钝角三角形.

【例4】 一个多边形的内角和比它的外角和的5倍少180°，求这个多边形的边数.

分析：因为任意多边形的外角和等于360°,则这个多边形内角和为5×360°-180°，利用多边形的内角和公式，结合问题中的相等关系，可得方程进行求解.

解析：设这个多边形的边数为n，则它的内角和是(n-2)•180°，外角和是360°，根据题意列得方程(n-2)•180°=5×360°-180°,解得n=11.