共顶点角问题分类探索

任南英

我们把顶点相同的角称为共顶点角，与共顶点角有关的问题一般可分为角的计数问题、角的大小计算问题、角的边的位置关系问题，所涉及的知识点是：角的和差倍分，互补、互余及对顶角等.

一、角的计数问题

由一个顶点发出若干条射线就可以组成一组共顶点角，这些角的个数一般与发出的射线条数有关，因为每两条射线及它所夹的平面部分就可以组成一个角，由此看来这些角的个数的计算与共线线段条数的计算方法一样(这也是由两个端点及端点所夹部分的线组成)，若线段上共有n个点(包括它的端点)可组成1/(2n)（n-1）条线段，同样从同一个顶点出发的n条射线(最大角小于平角)可以组成1/(2n)（n-1）个不同的角.

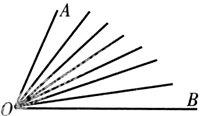
【例1】 如图，已知∠AOB内，由O点发出6条射线，共组成不同的角(包括∠AOB)有几个?

解析：从图中可看出包括∠AOB的两条边OA、OB在内图中共有8条射线，因此由这8条射线即n=8，共可组成不同的角共有1/(2n)（n-1）=1/2×8×(8-1)=28个.

说明：这类问题，得有一个前提最大角不超过180°,且所组成的角也只能是小于180°的角，否则就不行，想一想，为什么?

二、角的大小计算问题

1.角的和差倍分

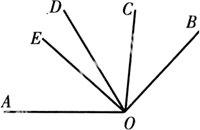
【例2】 如图，OC、OD、OE是∠AOB内的射线，OD平分∠AOB，OC平分∠BOD，∠DOE=13∠AOB，若∠COE=45°，求∠AOB的度数.

解析：设∠DOE=x°，则∠AOE=3x°，∠AOD=∠AOE+∠EOD=x°+3x°=4x°

∵OD平分∠AOB，

∴∠BOD=∠AOD=4x°.

又∵OC平分∠BOD，

∴∠COD=12∠BOD=12×4x=2x°,

∠COE=∠COD+∠DOE=2x°+x°=3x°,

由已知得∠COE=45°.

∴3x°=45°.

∴x=15.

又∠AOB=2∠AOD=8x°=8×15°=120°.

说明：一般在共顶点角问题中求角的大小均可采用设某个角的度数为未知数，从而可列出含未知数的方程来解，许多问题均可直接设所求角度为未知数(直接设法)，而本题却是间接设元法.

2.互余问题

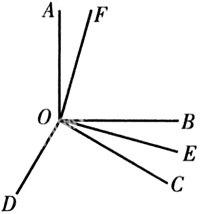
【例3】 已知OA⊥OB，OC⊥OD，OE⊥OF，∠AOD=146°，OE平分∠BOC，求∠AOF.

解析：设∠AOF=x,∵OA⊥OB,∴∠AOF+∠BOF=90°,

又∵OE⊥OF，∴∠FOB+∠BOE=90°，

∴∠BOE=∠AOF=x,

∵OE平分∠BOC，∴∠BOC=2∠BOE=2x,

而∠AOD+∠COD+∠BOC+∠AOB=360°，

∴146°+90°+2x+90°=360°,

解得x=17°,即∠AOF=17°.

说明：本题主要通过互余关系求解，当然还涉及周角问题；本题是采用直接设元法.

3.平角及互补问题

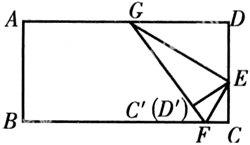
【例4】 如图，ABCD为一张长方形纸片，先找到长方形纸的宽DC的中点E，将∠C过E点折任意一个角，折痕为EF，使EC与EC′重合，再将∠D过点E折起，使DE和D′E重合，折痕为GE.

(1)∠FEC和∠GED′互为余角吗?为什么?

(2)上述折纸中，C点和D点折起之后，分别落在长方形的C′点和D′点.G、C′、D′和F是否在同一直线上?

解析：（1）∠FEC和∠GED′互为余角，由操作知，GE、EF分别是∠DEC′、∠CEC′的平分线.而∠DEC为平角，可知∠GEF=90°.因此，∠FEC和∠GED′互为余角.

（2）（略）.

说明：折叠问题的本质是轴对称，成轴对称的两个图形是全等图形.

4.对顶角

从例4中我们知道在两条直线相交所成的所有角中，有两组对顶角和4组邻补角.

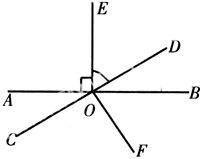
【例5】 如图,直线AB与CD相交于O，OB平∠DOF，OE⊥AB，O为垂足，∠1=50°，求∠AOC及∠COF.

解析：∵AB、CD相交于O，∴∠AOC=∠BOD，

又∵OE⊥AB,∴∠1+∠BOD=90°.

∴∠BOD=90°-∠1=90°-50°=40°,

∴∠AOC=40°.

∵OB平分∠DOF，

∴∠DOE=2∠BOD=80°，

∴∠COF=180°-∠DOF=180°-80°=100°.

5.平行线

在平行线的有关知识中，与共顶点角有关的知识不是比较多的，当然，一般的平行线中的共顶点角问题涉及到的知识点以对顶角居多，但也有一些问题例外，如下例题:

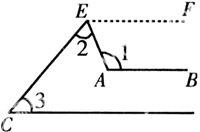
【例6】 如图，若AB∥CD，则（）.

A.∠1=∠2+∠3

B.∠1=∠3-∠2

C.∠1+∠2+∠3=180°

D.∠1-∠2+∠3=180°

解析：过E作EF∥AB，

∴∠1+∠AEF=180°，又∵EF∥AB，AB∥CD，∴EF∥CD，

∴∠3+∠CEF=180°,即∠3+∠2+∠AEF=180°.

∴∠1=∠2+∠3，故选A.

说明：本题看似无共顶点角，但在解题过程中，通过辅助线添加而得到与∠2共顶点的∠AEF，并通过∠AEF的过渡完成解答，得到结果，当然本题也可通过延长BA交CE于一点来求解.