等腰三角形中的角与周长
2008-09-27徐小芬
徐小芬
等腰三角形是三角形大家族中一个特殊而又重要的成员,也是中考中的重要考点之一.下面以中考题为例,说明有关的角与周长的计算.
例1(2007年•陕西)如图1所示,∠ABC=50°,AD垂直平分线段BC于点D,∠ABC的平分线BE交AD于点E.连接EC,则∠AEC的大小是_____.
解析:因为BE平分∠ABC,所以∠EBC=1/2∠ABC=25°.又AD垂直平分BC,所以EB=EC,所以∠C=∠EBC=25°.所以∠AEC=∠EDC+∠C=90°+25°=115°.
点评:本题综合考查了角平分线的性质、线段垂直平分线的性质以及等腰三角形的性质.若连接AC,易知△ABC为等腰三角形.∠AEC=∠AEB,在△ABE中也可算出结果.
例2(2007年•岳阳)已知△ABC中,AB=AC,∠B=60°,则∠A=_____.
解析:略.

例3(2007年•宁波)如图2,在△ABC中,AB=AC.CD平分∠ACB交AB于D点.AE∥DC交BC的延长线于点E.已知∠E=36°,则∠B=_____.
解析:因为AE∥DC,所以∠DCB=∠E=36°.因为CD平分∠ACB,所以∠ACB=2∠DCB=72°.又因为AB=AC,所以∠B=∠ACB=72°.
点评:△ACE也是一个等腰三角形.角平分线与平行线结合,往往出现等腰三角形.
例4(2007年•江西)如图3,在△ABC中,点D是BC上一点,∠BAD=80°.AB=AD=DC.则∠C=_____.
解析:因为AB=AD,∠BAD=80°,所以∠ADB=∠B=1/2(180°-80°)=50°.又因为AD=DC,所以∠C=∠CAD=1/2∠ADB=25°.
点评:本题综合考查了等腰三角形底角相等的性质以及三角形外角的性质.要注意等腰三角形的外角α与不相邻的内角β间的关系:α=2β或α+β=180°或180°+β=2α.它们可以互相表示.
例5(2006年•武汉)如图4,在△ABC中,AB的中垂线DE交AC于F,垂足为D.若AC=6,BC=4,求△BCF的周长.
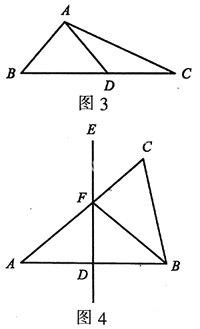
解析:因为DE垂直平分AB,所以FA=FB,所以△BCF的周长=BC+AC=4+6=10.
点评:本题利用线段垂直平分线的性质将△BCF的周长转化为BC+AC.这种转化技巧常常用到.
例6(2007年•安顺)如果等腰三角形的两边长分别为4和7,则三角形的周长为_____.
解析:因为已知的两边长没有确定是腰长还是底边长,故需分两种情况求解:当4为腰长时,第三边长为4,周长为4+4+7=15;当4为底边长时,第三边长为7,周长为4+7+7=18.综上可知,三角形的周长为15或18.
点评:在解答有关等腰三角形的边、角的问题时,几乎都要涉及分类讨论,所以一定要思考全面,小心谨慎!
