折叠与轴对称

任梦送

折叠型问题是近年中考的热点问题.通常是把某个图形按照给定的条件折叠，通过折叠前后图形的相互关系来命题.折叠型问题立意新颖，变幻多样.下面我们一起来探究这种题型的解法.

折叠型问题的规律是：折叠前后的部分图形，关于折痕成轴对称，两图形全等；对应点的连线被折痕垂直平分.同时，可以联合应用等腰三角形的性质和判定解决问题.

一、根据折叠性质求角的大小

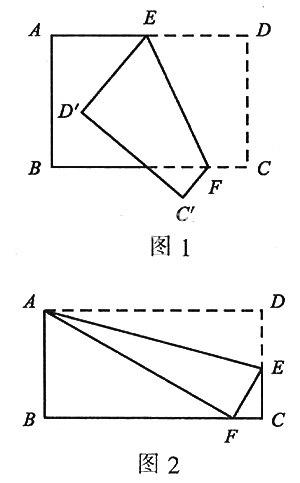
例1如图1，把一个长方形纸片ABCD沿EF折叠后，点D、C分别落在D′、C′的位置.若∠EFB=65°，则∠AED′=__.

解：把长方形这样折叠后，得到的四边形D′C′FE和四边形DCFE是全等的，根据全等形的性质，可得到∠DEF=∠D′EF.因AD∥BC，故∠DEF=∠EFB=65°.于是得到∠AED′=180°-2∠DEF=50°.

例2如图2，长方形ABCD沿AE折叠，使D点落在边BC上的F点处.若∠BAF=60°，则∠DAE=__.

解： 根据折叠的规律，可证△ADE≌△AFE，从而

∠DAE=∠FAE=（90°-60°）÷2=15°.

二、利用折叠得到特殊三角形

例3在一节数学活动课上，老师要求小明不借助任何工具在正方形的纸片上折叠出一个等边三角形.他折叠了一会儿，没有成功.你能帮他想想办法吗？

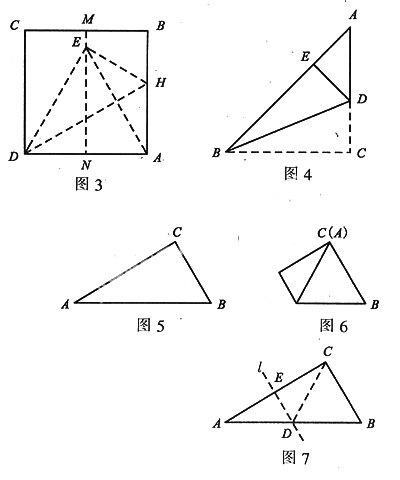
解：如图3，先把正方形纸片ABCD对折，再展开，折痕为MN.然后把AD边上的A点折叠到MN上的E点，折痕为DH.则△ADE即为等边三角形.

由折叠我们可以知道，MN是AD的垂直平分线.点E在MN上，则由△ADH≌△EDH，得DA=DE.又AE=DE，故△ADE为等边三角形.

三、求线段的长度

例4如图4，等腰Rt△ABC中，∠C=90°.沿着BD把点C折叠到AB上的E点.若△ADE的周长为10 cm，求AB的长.

解：根据折叠的规律可知△BCD≌△BED，所以BC=BE，DC=DE，△ADE的周长=DE+AD+AE=AC+AE=BC+AE=BE+AE=AB，所以AB=10 cm.

点评：利用对称转移线段，把三角形的周长放到一条直线上，是解这类周长、折叠结合问题的常用方法.

四、画出折痕

例5如图5，△ABC中，∠ACB=90°.将△ABC沿着一条直线折叠后，使A点与C点重合，如图6．

（1）请在图5中画出折痕所在的直线l．设直线l与AB、AC分别相交于点D、E，连接CD．

（2）通过观察、测量，请你找出完成题（1）后所得到的图形中的等腰三角形．（不要求证明）

解：（1）折痕为AC的垂直平分线.如图7.

（2）等腰三角形为△ACD、△BCD（因∠B=∠DCB）.

点评：折叠、垂直平分线总是紧密联系着的.

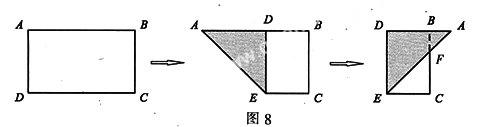
例6有一个矩形ABCD，AB=2.5，AD=1.5.将矩形折叠，使AD边落在AB边上，折痕为AE，再将△AED以DE为折痕向右折叠，AE与BC交于点F（如图8）.则CF的长为（）.

A. 0.5 B. 0.75C. 1D. 1.25

解：易知折叠后的∠DAE=45°.在最右边的图中，可计算出AB=2×1.5-2.5=0.5.从而BF=AB=0.5.故CF=AD-BF=1.5-0.5=1.选C.

点评：要能够从图形的两次折叠中发现边或角之间的关系，而从折叠出发得到∠DAE=45°是解题的关键.