四边形的“一般与特殊”，“性质与判定”

田载今

[一、四边形的“一般与特殊”]

在几何中，四边形的一般定义为：四条首尾相接的线段组成的图形叫做四边形.组成四边形的四条线段，叫做四边形的四条边.按照四条边是否共面，可以把四边形分为两类：四条边在同一平面内的四边形叫做平面四边形；四条边不在同一平面内的四边形叫做空间四边形.例如，把一张方形的纸铺平，它的四边就组成一个平面四边形；把这张纸沿对角线折一下，使对角线两旁的部分不在同一平面内，这张纸的四条边就组成了一个空间四边形（如图1）.初中数学中主要讨论平面四边形.

平面四边形又可以进一步分为两类：画出平面四边形的任意一条边所在直线时，如果整个四边形都在直线的同侧，则它是凸四边形（如图2（1））；否则它是凹四边形（如图2（2））.初中数学中讨论的四边形主要是凸四边形.

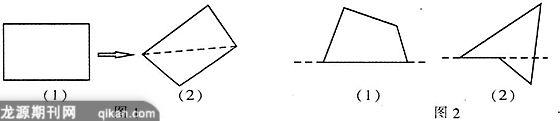
对于一般的四边形，四条边只要能够首尾相接即可，并无其他关于边的位置或长短的要求.梯形、平行四边形、矩形、菱形、正方形则不仅都是四边形，并且各自满足一定的附加条件.像这样满足一定附加条件的四边形称为特殊的四边形.进一步可以看出，矩形、菱形和正方形又是满足一定附加条件的平行四边形，即它们是特殊的平行四边形.

[二、四边形的“性质与判定”]

通常，教科书中在给出一种图形的定义后，会继续讨论由这个定义能进一步推出哪些结论，即得出这种图形的一些性质.这些性质往往是经常用到的主要性质.这种图形很可能还有一些其他性质，教科书则未曾涉及.例如，平行四边形除具有教科书中所说的“对边平行且相等”“对角相等”“对角线互相平分”等主要性质之外，还有“对角线的平方和等于四条边的平方和”这个性质.它可以证明如下.

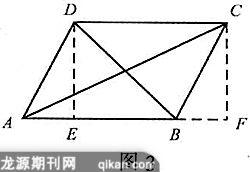
如图3，作▱ABCD的高线DE，CF. 利用全等三角形可以证明AE=BF.

AC²=AF²+CF²=（AB+BF）2+BC²-BF²=AB²+BC²+2AB·BF，①

BD²=BE²+DE²=（AB-AE）2+DA²-AE²=AB²+DA²-2AB·AE.②

∵AB=CD，AE=BF，

∴①+②，得AC²+BD²=AB²+BC²+CD²+DA².

实际上，图形的所有性质都是由图形定义所确定的.虽然定义本身并未直接表述出所有性质，但是定义中已经隐含了它们.故而以定义为出发点，可以逐步推导出所有性质.

图形的“性质”和“判定”，是两类不同的问题.讨论一种图形的性质，是在确定对象已经是这种图形的前提下进行的；讨论一种图形的判定，是为确定对象是这种图形而进行的.有时，在分析某个问题的过程中，两类问题都会出现，如先判定某对象是一种特定的图形，再推导出它的一些性质.

是不是只要一种图形有某条性质，就可以反过来把这条性质当成这种图形的一个判定条件呢？不是！并非一种图形的每个性质都可以拿来作为这种图形的判定条件.例如，正方形具有“对边平行，邻边相等”的性质，但是仅根据一个四边形满足“对边平行，邻边相等”不能判定它是正方形，而只能判定它是菱形.

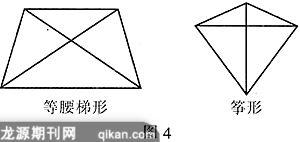
然而，“对边平行，邻边相等，邻角相等”是正方形所独有的性质，因此它能作为正方形的判定条件.又如，矩形具有“对角线相等”的性质，但是仅根据一个四边形的“对角线相等”并不能判定这个四边形是矩形.图4中的等腰梯形和筝形都是对角线相等的四边形，但它们不是矩形.如果一个四边形“对角线相等”且“对边平行”，则它一定是矩形，即一个四边形“对边平行，对角线相等”可以作为矩形的一个判定条件.总之，一种图形的判定条件，必须是只有这种图形才能够满足的条件.