利用抛物线方程方法计算目标RCS

2008-04-24方重华,易学勤,宋东安

中国舰船研究 2008年2期

1 引言

长期以来，目标RCS的计算一直是电磁领域研究的一大热点。相关的算法有很多，如高频近似方法中的GO、PO、GTD以及低频算法中的FDTD、FEM、MoM等[1]。其中的高频近似方法主要是针对电尺寸在数十个波长之上的目标计算效果较好，尺寸若进一步减小则结果精度难以保证；而低频算法则主要用于与波长相当(或小于)的目标计算中，虽然精度较高，但是随着目标电尺寸的增大，其计算需求按指数增长，以致计算时间量和所需内存极大。

抛物线方程方法首先是在计算地球表面的电磁波绕射时引入电磁计算之中[2]。近些年来，抛物线方程方法在电磁学和声学领域的散射计算之中展现出了独特的功效[3]，尤其是针对几个至几十个波长目标的散射特性计算相当有效。因此，在本文中，我们推导出抛物线方程方法关于目标RCS的计算表达式，最后计算了一个导体球的RCS,其结果与解析解符合得很好。

2 抛物线方程方法

本文主要处理三维的抛物线方程，在所有表达式中，时谐因子e-jωt一律略过不写出。对于水平极化的情况，电场E只有一个非零分量Ez；而垂直极化的情况，磁场H只有一个非零分量Hz。因此，我们可以用如下函数表征两种极化情况。

u(x,y,z)=ψ(x,y,z)exp(-ikx)

(1)

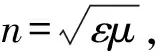
(2)

换用u表示，上式可变为:

(3)

这里，令

(3)

可以变为：

(4)

即

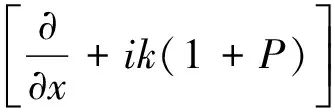
(5)

对式(5)进行分解可得如下一对方程。

(6a)

(6b)

式(6a)、式(6b)分别描述沿x轴正向和反向传播的电磁波。接下来，我们将利用二元函数的泰勒一阶展开来简化式(6a)。

令

(7)

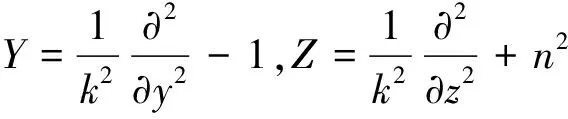
令式(7)做泰勒级数的一阶近似。

(9)

带入式(6a)中可得：

(10)

即

(11)

式(11)即标准的抛物线方程。可以将式(11)离散化以计算目标的RCS。积分域为包含目标的矩形体，边界条件设为PML(图1)。

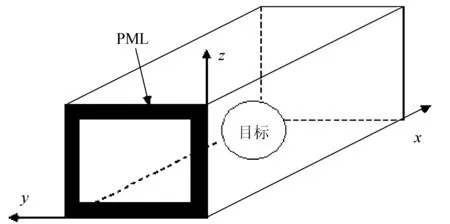
图1 积分域及PML吸收边界条件

因此，我们可以导出积分域内任一点x0总场的表达式：

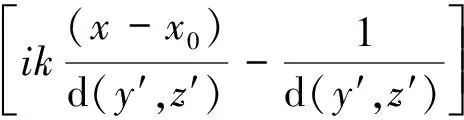
(12)

上式中，

RCS的表达式为：

(13)

式中，x=rcosθ，y=rsinθcosφ，z=rsinθsinφ。

如果我们假设入射波为单位强度的平面波，设θ，φ分别为入射波与y轴和z轴的夹角，表达式如下。

u(x,y,z)=exp(ik(x(cosθ-1)+

ysinθcosφ+zsinθsinφ))

(14)

再考虑到抛物线方程的傍轴近似，式(13)可以变为:

(15)

3 计算结果

为了证明抛物线方程方法的有效性，计算了一个半径为1 m的导体球的双站RCS。入射波频率为600 MHz,入射角为零度，即同轴向入射。如图2所示，抛物线方程方法和解析方法的结果吻合得相当好。在后向散射方向(即θ=0°)附近，二者完全一致，随着对轴向的偏离，θ变大，二者出现微小的偏差。然而，这个偏差显然是很小的，足以满足大多数情况下计算精度的要求。