数学中的排序原理

欧阳维诚

军事上“擒贼先擒王”的思想，对于解数学题非常有用。在研究数学问题时，常常要从考虑的对象中找到一个为首的元素，找出第一个为首的元素以后，再找第二个为头的，继续下去，第三个、第四个……用数学术语来说，就是把一个集合的所有元素，按某种原则依次排队，排队之后，常常有助于发现解决问题的途径。在数学中称这一思想为排序原理。

在许多数学问题中涉及一些可用数量来刻画的元素，如数的大小、线段的长短、角的大小等等。对于集合而言，不考虑元素之间的顺序。如果它们之间没有顺序，杂乱无章，往往会使许多有利于解题的条件被隐蔽起来，给解题带来困难。因此，有经验的解题者在解题之前，总是先考虑一下有没有必要给所涉及的集合的所有元素排一个顺序，无论是自然的顺序还是人为的顺序，常常都有助于解题。

请看下面一个简单的例子：

有１０人同时到一个服务窗口办事，假定这１０人需要服务的时间都是互不相同的，应该如何安排这１０人服务的次序，才能使他们１０人总的花费时间（包括每人被服务的时间和等待服务的时间）最少？

我们不妨把这１０人依次编号为

１，２，３，４，５，６，７，８，９，１０。

他们需要服务的时间依次是

ａ₁，ａ₂，ａ₃，ａ₄，ａ₅，ａ₆，ａ₇，ａ₈，ａ₉，ａ₁₀。

因为他们需要服务的时间互不相同，把需要服务时间最多的那个当作“王”，不妨假定ａ₁₀先“擒”出来。ａ₁₀取出之后，剩下的９个人又有一个需要服务时间最长的“王”，设它是ａ₉，把ａ₉“擒”出来。继续下去，每次“擒”住一个服务时间最长的“王”，设依次为₈ａ₇，…，ａ₁。

这样，我们用逐步“擒王”的办法，把１０个人依次需要的服务时间排成一个从大到小的次序：ａ₁₀＞ａ₉＞ａ₈＞ａ₇＞ａ₆＞ａ₅＞ａ₄＞ａ₃＞ａ₂＞ａ₁。直觉告诉我们，应该让服务时间最短的人先去接受服务。这样开始一齐等的人多，但服务的时间短，总的等待时间就少一些。到了后面，服务的时间越来越长，但同时等待的人也越来越少，总时间会短一些。

事实上也的确如此，用数学方法可以严格证明。

再看下面的例子：

某社区有若干幢建筑物，任何两幢的高度都不一样，任何两幢的距离都不超过它们的高度之差，如果最高的一幢建筑物的高度不超过１００米，那么我们一定可以用一道不超过２００米的围墙（不包括建筑物本身的长度）把这些建筑物围起来。

这个问题乍看起来似乎难以想像，这些建筑物的数量不明，布局未定，远近高低不同，围墙如何修法？我们可以请排序原理来帮忙。

假设共有ｎ幢建筑物，把它们从高到矮排一个顺序，设它们的高度依次是

１００≥ａ₁＞ａ₂＞ａ₃＞…＞ａ_n。

如图１所示，围墙从ａ₁筑到ａ₂，再从ａ₂到ａ₃，ａ₃到ａ₄，…，最后从ａ_n再回到ａ₁。由于任何两座建筑物之间的距离都不超过它们的高度之差，所以围墙从ａ₁到ａ_n的长度不会超过（ａ₁－ａ₂）＋（ａ₂－ａ₃）＋（ａ₃－ａ₄）＋…＋（ａ_n-1－ａ_n）。

（ａ₁－ａ₂）＋（ａ₂－ａ₃）＋（ａ₃－ａ₄）＋…＋（ａ_n-1－ａ_n）＝ａ₁－ａ_n＜ａ₁≤１００。整个围墙是从ａ₁到ａ_n的两倍，所以围墙的长度不会超过２００米，把所有建筑物都围住了。

最后，我们再利用排序原理，做一个简单的数学游戏。在９张小卡片上写下９个不同的整数ａ₁，ａ₂，…，ａ₉。甲、乙两人轮流取一张小卡片放在一个３×３的方格棋盘中的某一格，每一小格放一张卡片，不准多放，也不准不放。放完后，对甲计算最上一行和最下一行中的６张卡片上的６数之和，对乙则计算最左及最右两列的６数之和，和数大者为胜，问谁有获胜的策略？

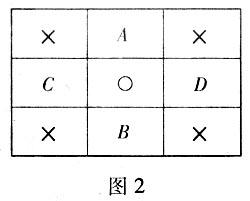
由图２可知，在计算胜负时，打“○”的中间一格里的数根本不用，因而不起作用。打“×”的四个小方格里的数，是甲、乙的公共数，所以不影响胜负。真正对甲、乙的胜负起作用的只有Ａ、Ｂ、Ｃ、Ｄ四格中的数。最简单的取胜思想自然是挑最大的数给自己，挑最小的数给对方。所以，首先要把９个数的大小排成一个顺序。

不妨假定９个数的大小顺序是

ａ₁，ａ₂，ａ₃，ａ₄，ａ₅，ａ₆，ａ₇，ａ₈，ａ₉。

我们只要考虑两个最大的ａ₈、ａ₉和两个最小的ａ₁、ａ₂就可以了，这要分三种情况讨论：

（１）若ａ₉－ａ₈＞ａ₂－ａ₁，这时先放者甲只要将最大的ａ₉放在Ａ格内，那么Ｂ格放的即使是最小的ａ₁，也会有Ａ＋Ｂ＝ａ₉＋ａ₁＞ａ₂＋ａ₈，甲必胜。

（２）若ａ₉－ａ₈＞ａ₂－ａ₁，这时先放者甲可将最小的ａ₁送给乙，放在Ｃ格处，下一步乙即使把最大的ａ₉放在Ｄ内，也会有Ｃ＋Ｄ＝ａ₁＋ａ₉＜ａ₂＋ａ₈，甲必胜。

（３）若ａ₉－ａ₈＞ａ₂－ａ₁，甲未必能胜，乙最多能和。因为若甲第一步取最大的ａ₉置于Ａ，第二步乙即可取最小的ａ₁放在Ｂ处。第三步、第四步，甲、乙都只能在Ｃ、Ｄ两格内分别放下ａ₂和ａ₈，总有Ａ＋Ｂ＝ａ₉＋ａ₁＝ａ₂＋ａ₈＝Ｃ＋Ｄ，甲、乙不分胜负。同样的，若第一步甲将最小的ａ₁送进对方的Ｃ处，第二步乙即可将最大的ａ₉放在自己的Ｄ格内，这时仍会有Ｃ＋Ｄ＝ａ₁＋ａ₉＝ａ₂＋ａ₈＝Ａ＋Ｂ，也不分胜负。所以，在这种情况下，如果双方不发生错误的话，总是和局。不发生错误的关键，就是要牢牢抓住最大的或最小的“王”。