基于并行混合模型的滚动轴承剩余寿命预测

准确地跟踪和预测滚动轴承剩余使用寿命，对于保障工业设备的安全性和可靠性具有重要的现实意义。针对现有模型在变工况下滚动轴承剩余寿命预测精度低、鲁棒性差的问题，提出一种基于并行混合模型的滚动轴承剩余寿命预测方法。引入添加SENet的多尺度卷积神经网络，提取滚动轴承退化阶段的深层特征；通过变分模态分解将所提特征分解为趋势项和随机项，分别输入到相关向量机和添加时序模式注意力机制的长短时记忆网络中进行预测，并选用瞪羚优化算法对预测模型的未知参数寻优；将所建模型应用于滚动轴承加速退化试验数据集。研究结果表明，相较于传统模型，该方法具有更高的预测精度和鲁棒性。研究结果可为滚动轴承的剩余寿命预测提供一种新的有效途径。

滚动轴承；剩余寿命预测；瞪羚算法；时序模式注意力机制；长短时记忆网络；相关向量机

TE832

A

DOI： 10.12473/CPM.202401022

RUL Prediction of Rolling Bearing Based on Parallel Hybrid Model

Tang Youfu" Li Ao" Liu Ruifeng" Jiang Peichen" Ding Han

（School of Mechanical Science and Engineering， Northeast Petroleum University）

Accurately tracking and predicting the remaining useful life （RUL） of rolling bearings is of great practical significance for ensuring the safety and reliability of industrial equipment. The existing models demonstrate low accuracy and poor robustness in predicting the RUL of rolling bearings under variable operating conditions. This paper presents a rolling bearing RUL prediction method based on parallel hybrid model. First， a multi-scale convolutional neural network （MSCNN） with SENet was introduced to extract the deep features of rolling bearing at degradation stage. Second， the proposed features were decomposed into trend terms and random terms by variational mode decomposition （VMD）， and input into a related vector machine （RVM） and a long short-term memory network （LSTM） with temporal pattern attention mechanism （TPA） for prediction. Third， the gazelle optimization algorithm （GOA） was used to optimize the unknown parameters of the prediction model. Finally， the built model was applied to the accelerated degradation test data set of rolling bearings. The research results show that compared with conventional models， this method has higher prediction accuracy and robustness. The research results provide an effective way for the RUL prediction of rolling bearings.

rolling bearing;RUL prediction;GOA;TPA;LSTM;RVM

基金项目：东北石油大学青年科学基金项目“齿轮齿条钻机起升系统与受压钻柱非线性耦合动力机理研究”（2018QNL-28）。

0" 引" 言

滚动轴承作为高铁、汽轮机、航空发动机等高速、重载装备的关键承载部件，服役的工况尤为恶劣，极易产生磨损、裂纹、点蚀等缺陷，进而引发机械系统整体工作性能和结构的危害，带来严重的经济损失，甚至危及人员安全。因此，亟需对滚动轴承进行全生命周期的实时状态监测，并对其剩余使用寿命（Remaining Useful Life，RUL）进行精准预测，为设备的预测性维护提供可靠依据。

在如今大数据背景下滚动轴承监测数据多呈现非线性、多样性以及多维度的特点，如何从庞大的数据中挖掘有用信息是滚动轴承RUL预测的关键。深度学习算法拥有强大的特征提取能力、非线性拟合能力，能更好地处理多元化的滚动轴承性能衰退数据，大量深度神经网络被开发并应用于滚动轴承RUL预测。聂磊等［1］从时域、频域、时频域等不同层面提取滚动轴承退化特征组建特征集，并经过特征筛选与主成分分析（Principal Components Analysis，PCA）融合，将融合特征输入到卷积神经网络（Convolutional Neural Network，CNN）中进行预测，试验结果表明，该方法具有较高的预测精度，但是上述过程人工干预性强，效率较低。莫仁鹏等［2］将残差网络用于滚动轴承的RUL预测，缓解了CNN深度过大引发的梯度弥散以及网络退化现象。滚动轴承退化数据中蕴含了大量的时序信息，CNN虽然拥有强大的高维特征提取能力，但对时序信息的记忆能力较弱。H.HOTAIT等［3］将长短时记忆网络（Long Short-Term Memory Network，LSTM）用于滚动轴承RUL预测，结果表明，该模型相较于传统回归模型更适用于非线性时间序列的预测。M.MAREI等［4］结合CNN和LSTM用于刀具的RUL预测，试验验证该方法相较于单一的LSTM具有更高的泛化能力。

目前，对于较长时序数据的预测，LSTM容易丢失重要序列信息。在变工况下，LSTM的预测精度和鲁棒性还有待提升。同时基于深度学习的RUL预测方法得到的结果通常仅为点估计，而设备性能退化受到环境、负载等多重随机因素影响， 导致RUL预测结果不可避免地具有不确定性，因此无法直接应用于后续的维修决策。针对上述问题，本文提出一种基于并行混合模型的滚动轴承RUL预测方法。首先，提取滚动轴承振动信号12个时域特征、3个频域特征以及8个3层小波包节点能量组成特征集，通过由单调性、时序相关性以及鲁棒性加权组成的综合指标对特征集筛选；其次，在RMS指标上利用自上而下（Top-Down，TPD）的方法找到退化起始点与失效点，将滚动轴承全寿命周期划分为健康阶段、退化阶段、失效阶段；再次，将退化阶段特征集数据输入到添加SENet的多尺度卷积神经网络（Multi-Scale Convolutional Neural Network，MSCNN）中进行深度特征提取，得到多尺度、深层次的表征滚动轴承衰退规律的退化因子；从次，使用变分模态分解（Variational Mode Decomposition，VMD）将退化因子分成趋势项与随机项，将趋势项输入到相关向量机（Relevance Vector Machine，RVM）中预测，将随机项输入到添加时序模式注意力机制（Temporal Pattern Attention Mechanism，TPA）的LSTM中预测，并选用瞪羚优化算法（Gazelle Optimization Algorithm，GOA）对预测模型未知参数寻优；最后，在预测模型的基础上融合分位数回归，从而获得不同分位数下的滚动轴承RUL预测组成预测区间，实现滚动轴承RUL区间概率预测。

唐友福，等：基于并行混合模型的滚动轴承剩余寿命预测

1" 滚动轴承RUL预测模型理论分析

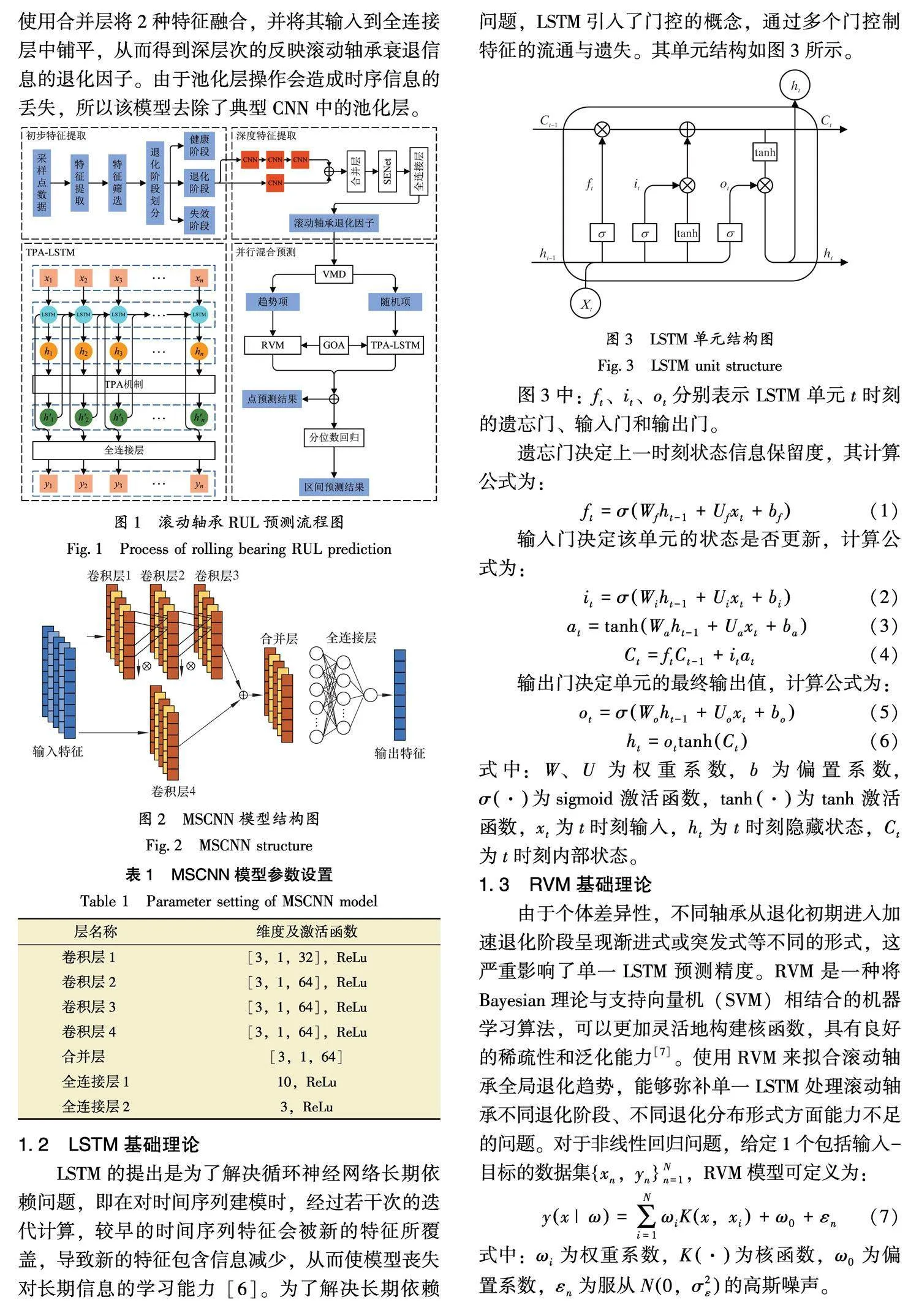
不同工况、不同型号的滚动轴承呈现显著的退化趋势差异。滚动轴承衰退曲线在全局具有长期关联性，在局部表现为随机波动性。长期关联性是指滚动轴承退化数据在较长的时间段内存在数值关联；随机波动性是指其局部波动具有非线性的特点，并且随着时间推移，波动更为剧烈。这些特性极大地增加了预测难度。针对该问题，提出一种基于并行混合模型的滚动轴承RUL预测方法，该方法的整体流程如图1所示。

1.1" MSCNN基础理论

CNN是一种通过卷积运算处理多维数据的深度神经网络，因其强大的特征提取能力被广泛应用于故障诊断和寿命预测［1］等领域。传统的CNN包括卷积层、池化层、全连接层3个主要部分。首先通过卷积层提取输入数据中的显著特征，然后利用池化层降低特征的空间维度，最后借助全连接层将特征展平成一维序列。文献［5］指出，增加CNN的深度可以提取滚动轴承的全局时序退化特征。对此，建立MSCNN模型结构如图2所示，模型参数设置如表1所示。

通过卷积层1～3提取输入特征的全局退化信息，通过卷积层4提取输入特征的局部波动信息，使用合并层将2种特征融合，并将其输入到全连接层中铺平，从而得到深层次的反映滚动轴承衰退信息的退化因子。由于池化层操作会造成时序信息的丢失，所以该模型去除了典型CNN中的池化层。

1.2" LSTM基础理论

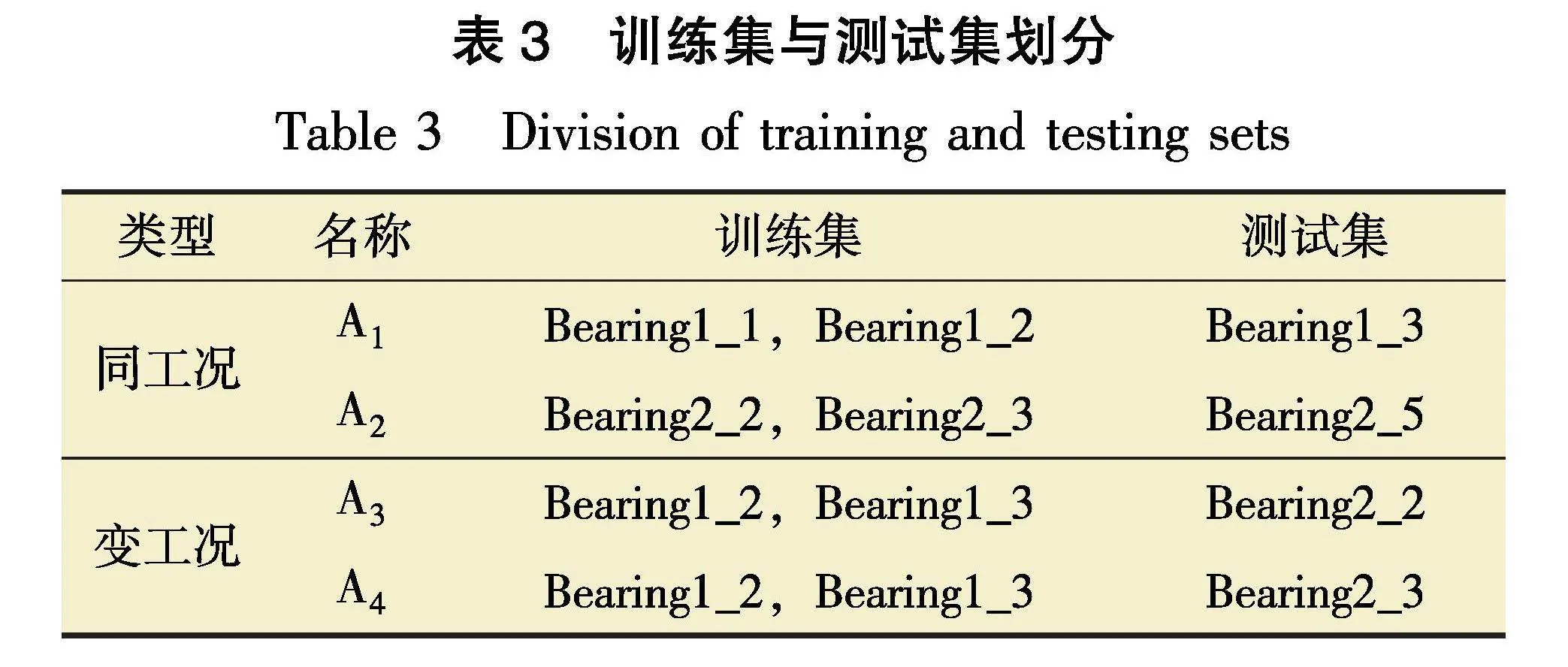
LSTM的提出是为了解决循环神经网络长期依赖问题，即在对时间序列建模时，经过若干次的迭代计算，较早的时间序列特征会被新的特征所覆盖，导致新的特征包含信息减少，从而使模型丧失对长期信息的学习能力［6］。为了解决长期依赖问题，LSTM引入了门控的概念，通过多个门控制特征的流通与遗失。其单元结构如图3所示。

图3中：ft、it、ot分别表示LSTM单元t时刻的遗忘门、输入门和输出门。

遗忘门决定上一时刻状态信息保留度，其计算公式为：

ft=σWfht-1+Ufxt+bf（1）

输入门决定该单元的状态是否更新，计算公式为：

it=σWiht-1+Uixt+bi（2）

at=tanhWaht-1+Uaxt+ba（3）

Ct=ftCt-1+itat（4）

输出门决定单元的最终输出值，计算公式为：

ot=σWoht-1+Uoxt+bo（5）

ht=ottanhCt（6）

式中：W、U为权重系数，b为偏置系数，σ·为sigmoid激活函数，tanh·为tanh激活函数，xt为t时刻输入，ht为t时刻隐藏状态，Ct为t时刻内部状态。

1.3" RVM基础理论

由于个体差异性，不同轴承从退化初期进入加速退化阶段呈现渐进式或突发式等不同的形式，这严重影响了单一LSTM预测精度。RVM是一种将Bayesian理论与支持向量机（SVM）相结合的机器学习算法，可以更加灵活地构建核函数，具有良好的稀疏性和泛化能力［7］。使用RVM来拟合滚动轴承全局退化趋势，能够弥补单一LSTM处理滚动轴承不同退化阶段、不同退化分布形式方面能力不足的问题。

对于非线性回归问题，给定1个包括输入-目标的数据集xn，ynNn=1 ，RVM模型可定义为：

yx|ω=∑Ni=1ωiKx，xi+ω0+εn（7）

式中：ωi为权重系数，K·为核函数，ω0为偏置系数，εn为服从N0，σ2ε的高斯噪声。

由于yn独立分布，于是数据集的似然函数可以写成：

pyn|ω，σ2=2πσ2-N/2exp

-12σ2yn-Φω2（8）

式中：Φ=Kx，xiNi=1，为N×N维的核函数矩阵。

根据Bayesian定理，ω的后验概率分布为：

pω|yn，αi，σ2=2π-（N+1）/2∑-1/2×

exp-ω-μT∑-1ω-μ/2

（9）

∑=σ2ΦTΦ+A-1（10）

μ=σ-2∑ΦTyn（11）

式中：αi为超参数向量，∑为后验协方差矩阵，A=diagα1，α2，…，αN，μ为模型均值。

利用最大似然估计求得超参数α和σ2的估计值α︿和σ︿2，并通过不断迭代确定超参数的最优解：

α︿i=1-αi∑iiμ2i（12）

σ︿2=yn-Φμ2N-∑Ni=01-αi∑ii（13）

式中：∑ii为∑的第i个对角元素。

1.4" 特征提取

1.4.1" SENet基础理论

不同特征隐含的退化信息存在差异性。为了使MSCNN能够自适应分配各特征的权重，抑制冗余特征和噪声对后续预测过程的干扰，添加了SENet。

SENet能够提取特征信息的重要程度并增加重要特征对输出值的贡献率，降低次要特征的权重，减小模型的计算量。其主要包括挤压、激励和权重重构3部分操作［8］，模块结构如图4所示。

挤压操作：通过全局平均池化将每个通道的特征压缩成一个权重因子，进而量化特征的重要性。

激励操作：首先通过第1个全连接层将通道数降为原来的1/2，然后使用ReLu函数非线性激活，最后通过第2个全连接层恢复到初始通道数。该操作使得权重因子更具非线性，从而提高模块的泛化能力。

权重重构：利用Sigmoid函数对权重因子归一化，然后与输入加权相乘，从而起到强化重要特征的作用。

1.4.2" TPA基础理论

TPA首先使用多个一维卷积核从LSTM输出的隐藏状态ht中提取时序特征，然后通过评分函数确定当前时刻ht与以往时刻ht-w的权值，最后根据权值计算当前时刻最终的隐藏状态h′t［9］。TPA增强了LSTM对关键时刻输入值的敏感性，进而强化其对关键时序特征的记忆能力。TPA结构框图如图5所示。

CNN提取时序特征矩阵HCi，j：

HCi，j=∑wi=1Hi，t-w-1+l×Cj，T-w+l（14）

计算时序模式权重向量vt：

fHCi，ht=HCiTWaht（15）

αi=σfHCi，ht（16）

vt=∑mi=1αiHCi（17）

计算当前时刻隐藏状态h′t：

h′t=Wh′Whht+Wvvt（18）

式中：Hi，t+w-1+l=ht-w，ht-w+1，…，ht-1；w为关注的时间序列长度；Cj，T-w+l为卷积核；T表示卷积核尺寸；Wi，h′，h，v为权重的矩阵。

1.5" GOA算法优化过程

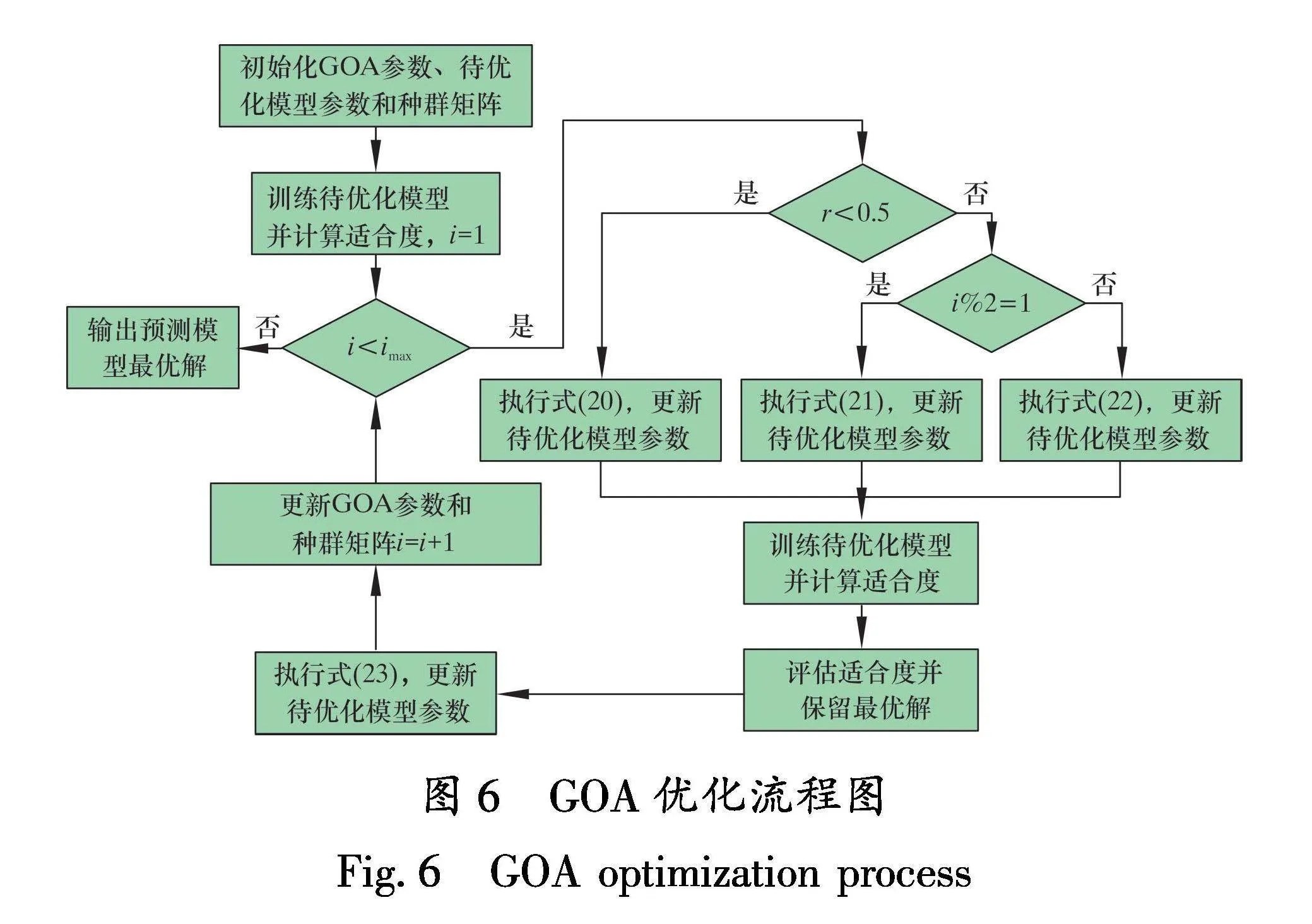
GOA算法是受瞪羚逃避捕食者行为的启发而提出的一种新型全局智能寻优算法［10］。相比于其他优化算法，GOA具有更高效的寻优效率以及更强大的收敛功能。GOA的基本建模步骤如下：

（1）种群随机初始化。

X=x1，1" …" x1，2" …" x1，d

x2，1" …" x2，2" …" x2，d

xn，1" …" xn，2" …" xn，d

（19）

式中：n表示瞪羚种群数目；d表示待优化问题维度；xi，j=r·Uj-Lj+Lj；r为［0，1］之间的随机数；Uj和Lj分别为待优化参数的上界和下界。

（2）全局搜索。

当瞪羚没有发现捕食者时采取自由放牧，此时瞪羚做布朗运动，其位置更新如下：

yi+1=yi+v·R·RB·Xi-RB·yi（20）

式中：yi+1为第i+1次迭代的解；y为第i次迭代的解；v表示瞪羚的移动速度；R为［0，1］之间的随机数组成的向量；RB为布朗运动的随机数向量。

（3）局部搜索。

当瞪羚发现捕食者后逃跑动作分为2个阶段。

第1阶段为瞪羚发现捕食者的前期，采取Levy飞行，其位置更新如下：

yi+1=yi+v·R·RB·Xi-RB·yi（21）

式中：RL为Levy分布的随机数向量，即Levyα=0.05ab-1a，a=N0，σ2a，σa=Γ1+αsinπα/2Γ1+α/2α2α-1/21α，b=N0，σ2b，σb=1 ，α=1.5 。

第2阶段为羚羊发现捕食者的后期，采取布朗运动，其位置更新如下：

yi+1=yi+v·μ·CF·RB·Xi-RL·yi（22）

式中：μ为-1或1，表示2种运动方向；CF=1-i/imax2i/imax，表示捕食者的累计效应。

（4）瞪羚逃生。

捕食者的狩猎成功率为34%，则瞪羚逃生过程数学模型如下：

yi+1=yi+CFL+R·U-L·d" r≤0.34

yi+0.34·1-r+ryr1-yr2r＞0.34

（23）

式中：d=0" r＜0.341" r=0.34；r1和r2为［imin，imax］之间的随机整数。

GOA算法优化流程如图6所示。

2" 试验研究

2.1" 数据集介绍

数据源自XJTU-SY滚动轴承加速寿命试验数据集［11］，数据采集试验台如图7所示。由2个单向加速度传感器分别测得横向和纵向2类振动信号，采样频率为25.6 kHz，采样间隔为1 min，每次采样时长为1.28 s。该数据集包括3个工况下共15个轴承的全寿命振动加速度数据。由于试验施加的力为径向力，所以水平方向的振动信号包含更多的轴承退化信息［12］。这里选用水平方向数据作为研究对象。

2.2" 滚动轴承初步特征提取及筛选

为了多层次的量化滚动轴承退化趋势，提取滚动轴承振动信号12个时域特征{平均值、标准差、偏度、峭度、最大值、最小值、峰峰值、均方根、振幅因子、波形因子、冲击因子、裕度因子}、3个频域特征{重心频域、平均频域、频域均方根}以及8个小波包节点能量共23个特征构建特征集，记作F1～F23。为了削弱短期随机波动和噪声对特征的影响，突出特征的长期趋势，对滚动轴承所有特征进行滑动平均处理（Moving Average，MA），滑动窗口取30。最后对特征集归一化处理。

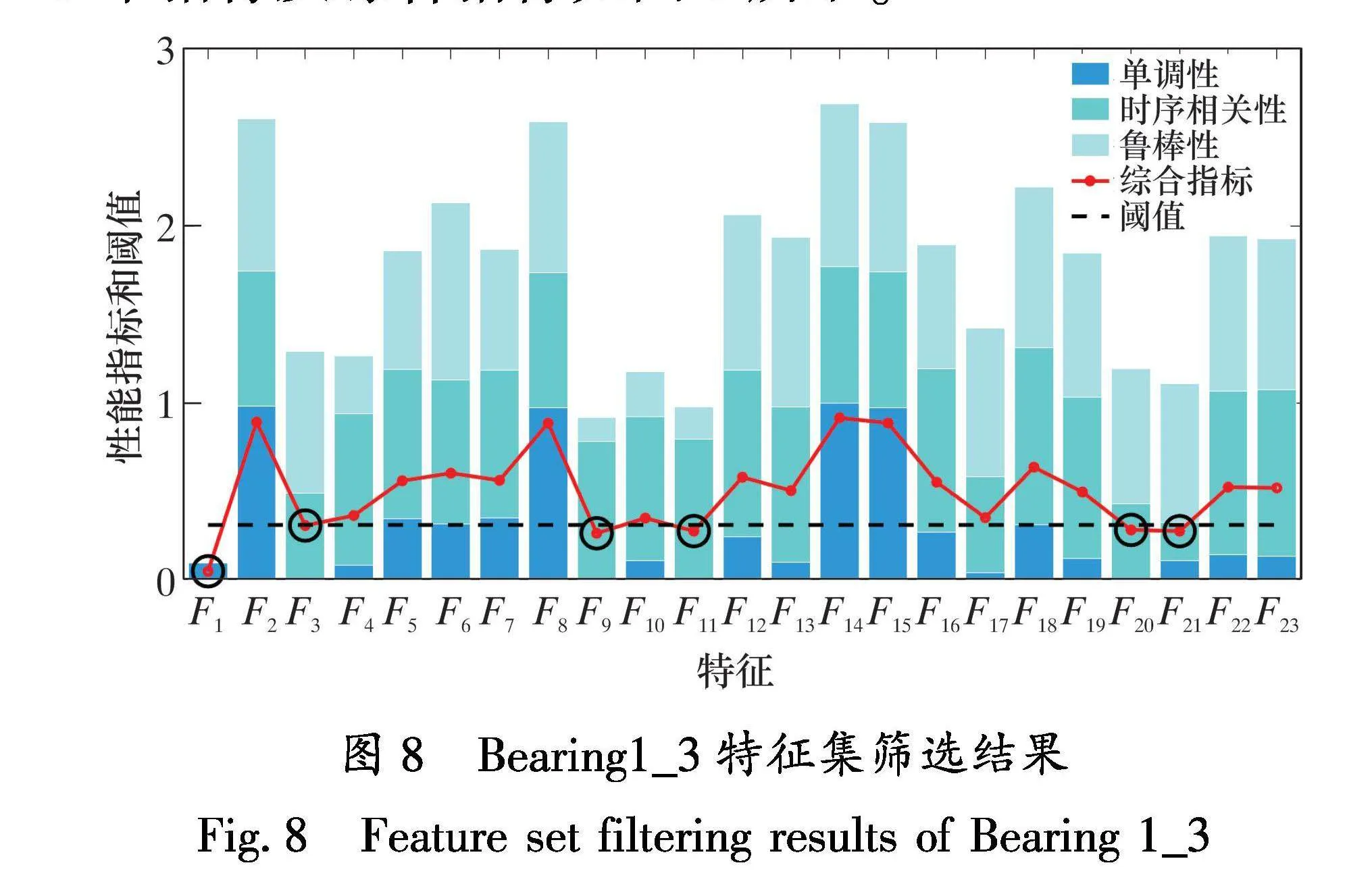
特征集中存在无法表征滚动轴承衰退规律和受噪声污染严重的特征，本文选用由单调性、时序相关性和鲁棒性加权组成的综合指标对原始特征集筛选［13］。其中单调性越高，表示特征值随时间持续增长或下降的趋势越大；时序相关性越高，表示特征序列与时间序列之间相关程度越强；鲁棒性越高，表示特征序列对异常值的容忍度越高。分别求得23个特征的单调性、时序相关性和鲁棒性指标。由于3个性能指标均为相对量，所以要先将其最大-最小缩放到［0，1］之间，再求综合指标。鉴于单调性更能反映滚动轴承随着时间推移退化速率逐渐升高的规律，3个指标的权重取0.5、0.3、0.2。将综合指标小于阈值的特征筛掉，筛选阈值由3σ准则确定。Bearing1_3特征集中23个特征的3个指标及综合指标如图8所示。

2.3" 基于TPD的滚动轴承阶段划分

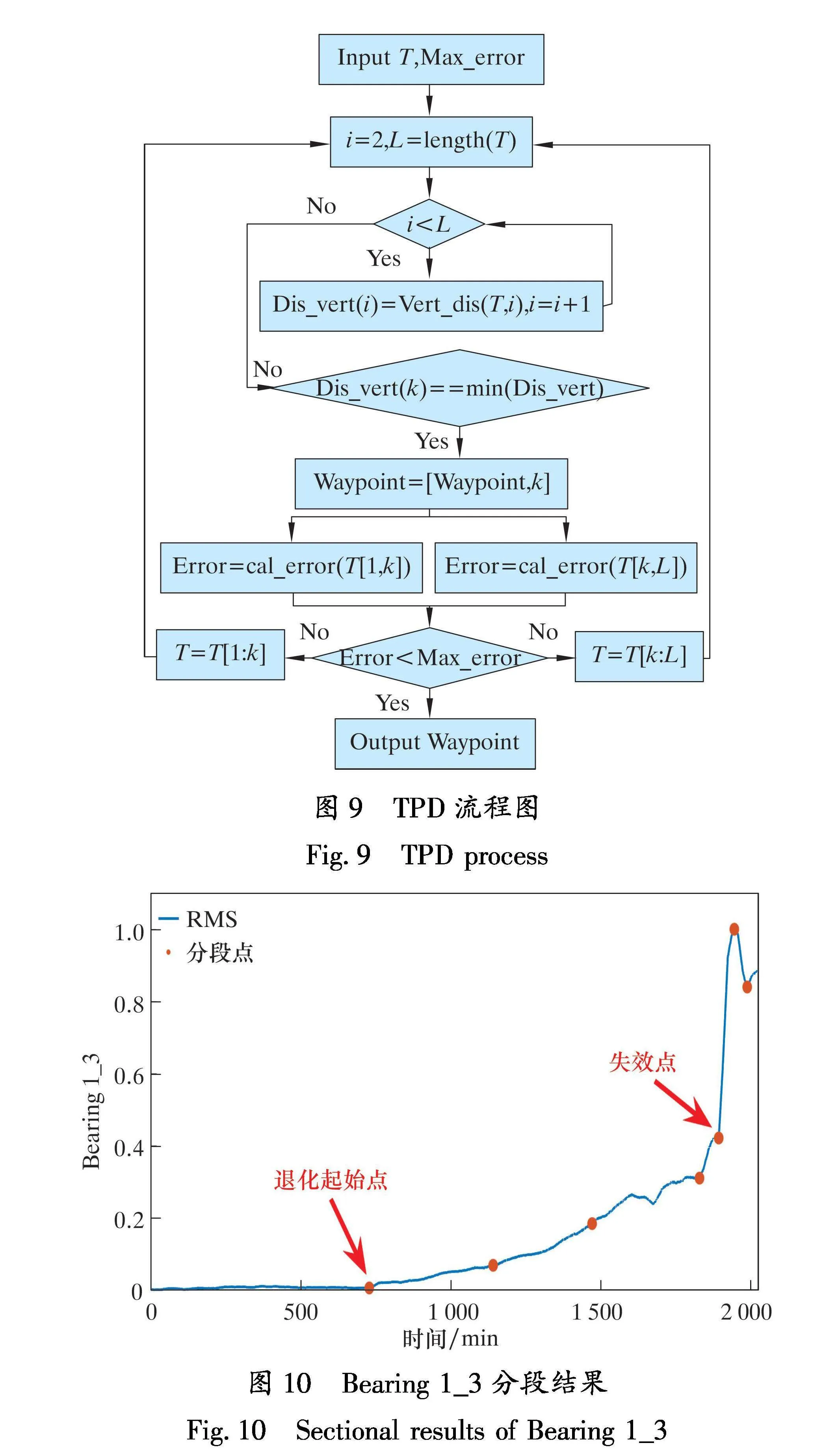
滚动轴承健康阶段携带极少的退化信息，失效阶段失去了维修的意义，所以仅对退化阶段进行预测。目前常用的阶段划分方法为3σ准则，但该方法对突变点较为敏感，当滚动轴承健康状态曲线具有较大的随机波动，使用该方法极可能较早地误判退化监测点。对此，在RMS指标上使用TPD找到退化起始点与失效点［14］，该方法流程如图9所示。

图9中，Max_error为循环停止阈值，本文取3.12×10-4。通过cal_error（T［a， b］）求得T在［a， b］区间的线性拟合误差，Vert_dis（T， i）=cal_error（T［1， i］）+cal_ error（T［i， end］）。利用TPD算法得到一系列分段点，选取第一个分段点为滚动轴承退化起始点，选取RMS最大值前一个分段点为滚动轴承失效点。图10为Bearing 1_3基于TPD算法的分段结果。

由图10可知，经过TPD分段，滚动轴承不同阶段的衰退速率存在明显差异，证明该方法可有效应用于滚动轴承阶段划分。

2.4" 基于SENet-MSCNN滚动轴承深度特征提取

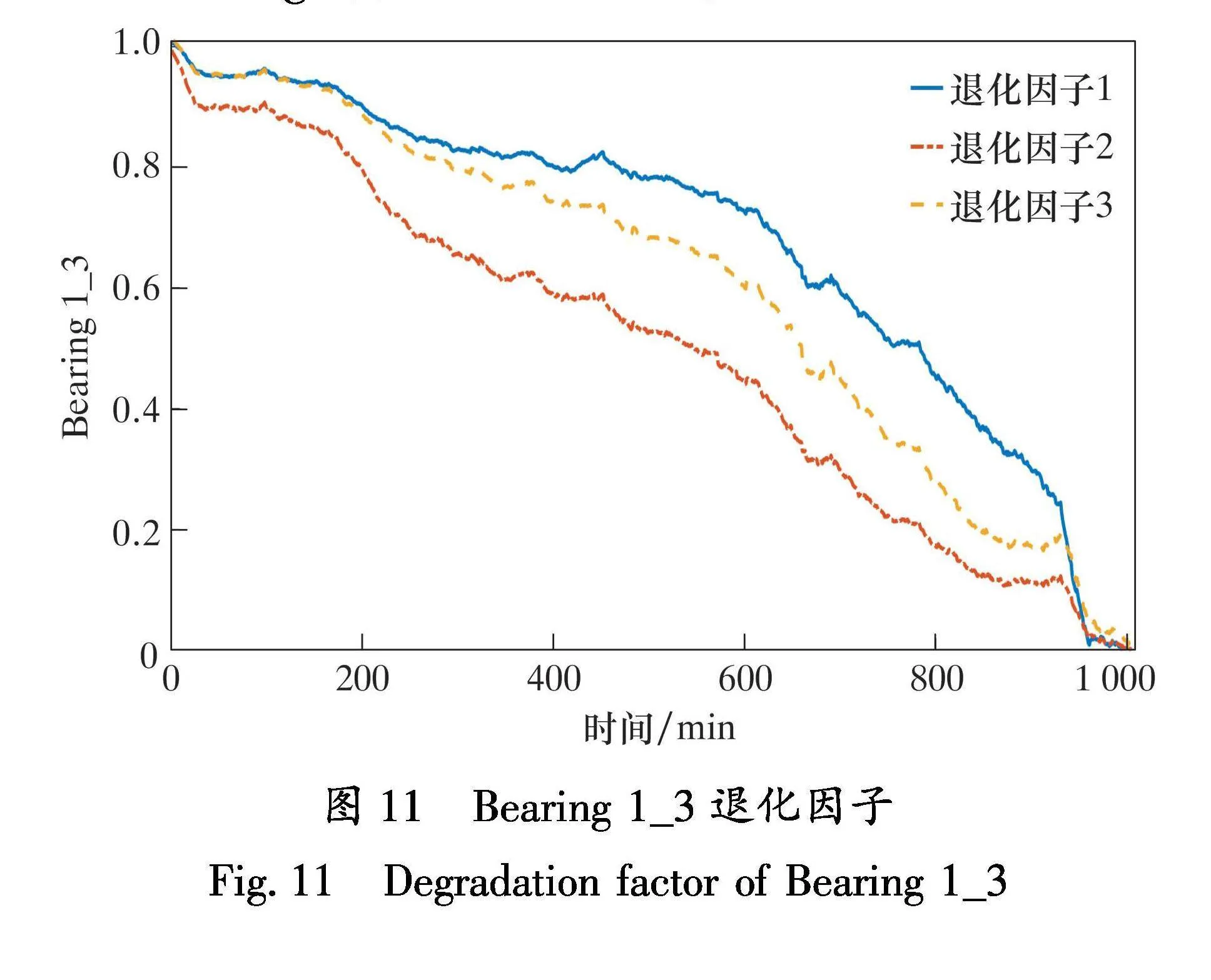
将滚动轴承退化阶段特征集归一化后输入到SENet-MSCNN模型中进行深度特征提取［15-16］。图11为Bearing 1_3的退化因子。

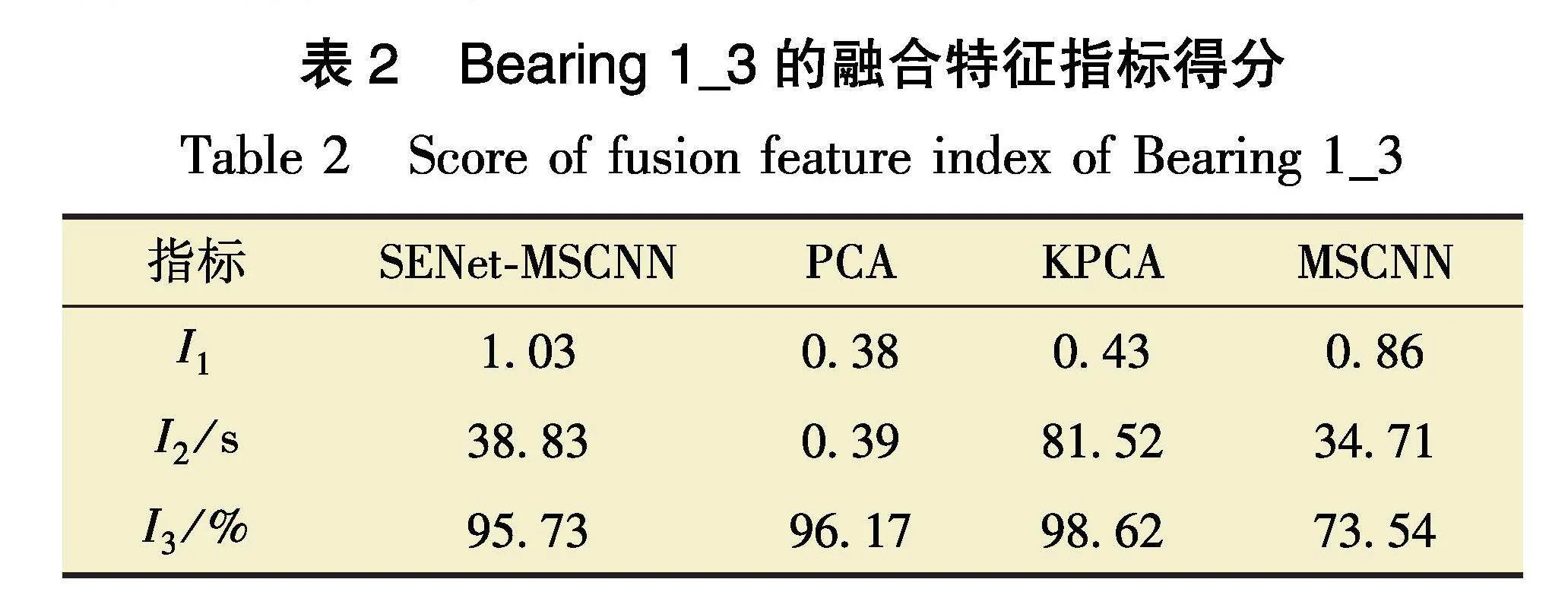
为了进一步验证该方法的有效性，将该方法与PCA、核主成分分析（Kernel Principal Component Analysis，KPCA）、MSCNN进行对比，同时选取平均单调性、耗时、累计解释方差作为评价指标，记作I1、I2、I3。其中累计解释方差越大，特征信息损失量越少，计算公式为100%×降维后特征总方差/降维前特征总方差。表2为Bearing 1_3的融合特征指标得分。

由表2可知：PCA和KPCA在降维过程中具有较少的信息损失，但无法保证融合特征的单调性；基于MSCNN提取的退化因子虽具有较高单调性，但特征信息损失较为严重；而基于SENet-MSCNN提取的退化因子具有较高的平均单调性和累计解释方差，表明SENet可以增强MSCNN的特征提取能力，并为后续模型的稳定预测提供有力支持。

2.5" 滚动轴承RUL预测结果及讨论

2.5.1" 模型参数设置

为了验证本文所提并行混合预测模型的有效性，将该方法与RVM、CNN、LSTM、TCN、TPA-LSTM模型预测结果进行对比，记作M0～M5。其中：并行混合模型结构如图1所示；对照模型RVM与本文RVM模块结构一致；CNN由2层卷积层和1层全连接层组成；LSTM由1层LSTM层、1层遗忘层和1层全连接层组成；TCN模型结构见文献［17］；对照模型TPA-LSTM与本文TPA-LSTM模块结构一致；所有模型未知参数均使用GOA寻优。训练集与测试集划分如表3所示。

VMD可将信号按照频率由低到高分解成n个准正交的模态分量，而滚动轴承全局退化信息多集中于低频段，随机波动信息多集中于高频段，因此VMD可将滚动轴承退化因子分解为趋势项和随机项。根据对VMD参数多次尝试寻优，设定模态分解数为6，惩罚因子为1 500，对滚动轴承退化因子进行模态分解。将前2项低频模态分量作为趋势项输入到RVM中进行预测，将后4项高频模态分量作为随机项输入到TPA-LSTM中进行预测。

选取高斯核函数和多项式核函数加权组合成的混合核函数作为RVM的核函数，公式如下：

s.t." 0＜λ＜1" λ∈R

Kxi，xj=λK1xi，xj+1-λK2xi，xj（24）

K1xi，xj=exp-xi-xj22σ2（25）

K2xi，xj=xi，xj+1n（26）

TPA-LSTM模型设定输入层通道数为3，损失函数为均方误差，选用Adam对损失函数优化，TPA关注序列长度为50，标签表达式如下：

yi=N-iN" i∈1，N（27）

GOA算法设定种群数为20，最大迭代次数为15，适应度值为真实值与预测值的均方误差。待优化参数包括式（24）、式（25）、式（26）中的λ、σ、n，TPA-LSTM的单元数、最大迭代次数、初始学习率、L2正则化参数。为了验证GOA参数寻优的有效性，将该方法与粒子群优化（Particle Swarm Optimization，PSO）［16］、鲸鱼优化（Whale Optimization Algorithm，WOA）［17］、麻雀优化（Sparrow Search Algorithm，SSA）［18］算法进行对比，各优化算法参数设置一致。图12为数据A1的4种优化算法对TPA-LSTM预测模型的优化过程适应度曲线。由图12可知，PSO、WOA、SSA分别在迭代11次、9次、8次后趋于平稳，而GOA在迭代6次后趋于平稳，并且在各算法迭代结束后，GOA的适应度值最小，证明GOA拥有更高效的寻优效果。表4为基于GOA的待优化参数寻优结果。

four optimization algorithms of Data A1

使用均方根误差（ERMS）和决定系数（R2）作为预测结果的评价指标。计算方法如下：

ERMS=101T∑Ti=1yi-y︿12（28）

R2=1-∑Ti=1yi-y︿12∑Ti=1yi-y—12（29）

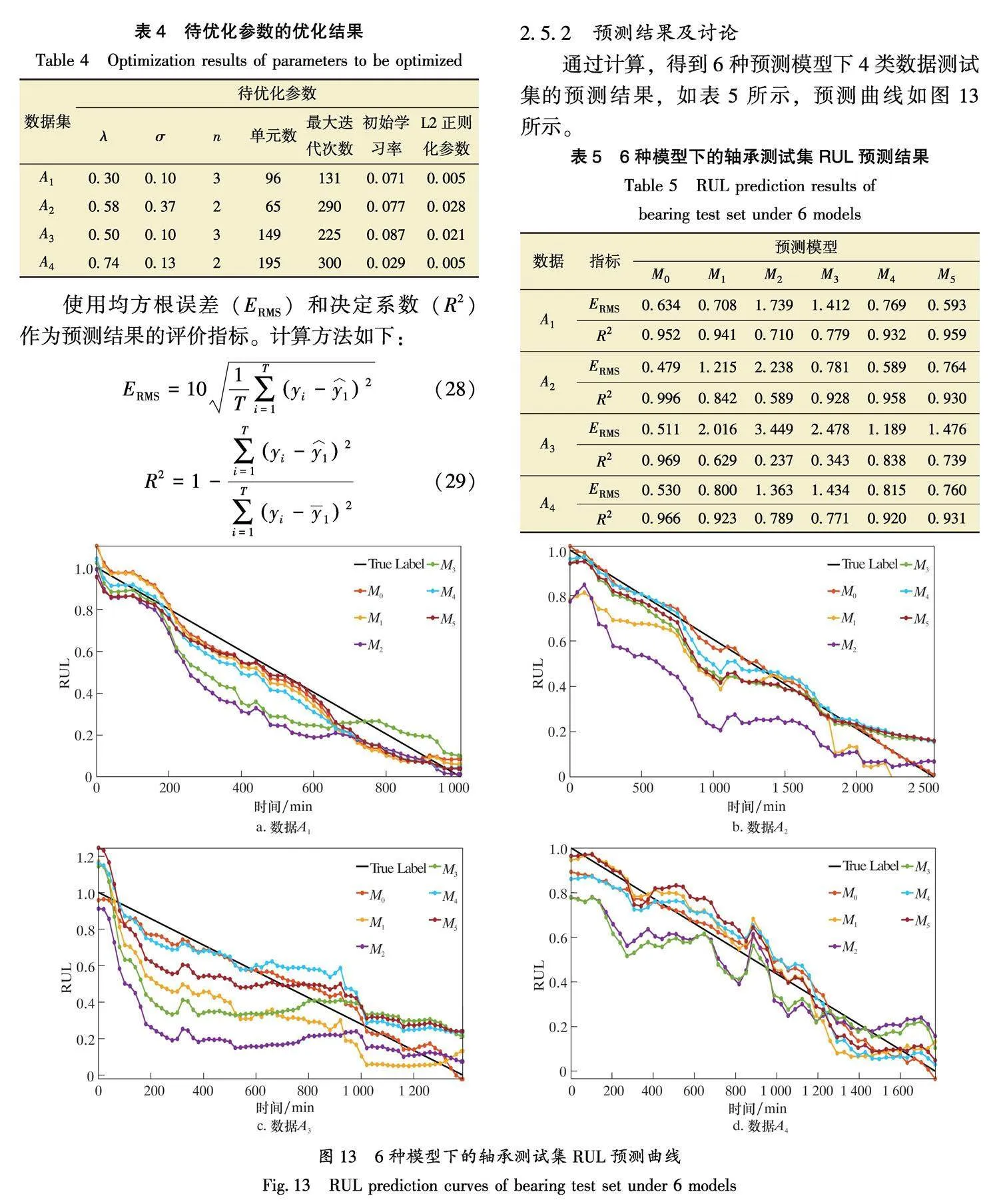
2.5.2" 预测结果及讨论

通过计算，得到6种预测模型下4类数据测试集的预测结果，如表5所示，预测曲线如图13所示。

结合表5和图13可知，当数据中存在随机波动时，RVM的预测结果不稳定。单一的LSTM模型的预测精度要高于单一的CNN模型。添加TPA的LSTM预测精度相对于传统LSTM得到大幅度提升。对比数据A3和数据A4的预测结果可知，对于变工况下的滚动轴承RUL预测，TPA-LSTM和TCN模型的预测结果不稳定，而本文所提并行混合模型在4种数据集下的ERMS均集中在0.55附近，证明本文该模型在变工况下具有较高的鲁棒性以及预测精度。

为了量化模型的预测不确定性，进一步探究本文方法的有效性，将分位数回归与并行混合模型融合，从而得到不同分位数下的滚动轴承RUL预测，组成预测区间。融合后预测模型的目标函数如下：

Lqyi，yqi=∑ni=1qyqi-yi+q-1yqi-yi（30）

式中：yi为真实值，yqi为分位数q下的预测值。

为了得到模型预测的90%置信区间，q取值为［0.1∶0.1∶0.9］，共9条预测曲线组成置信区间。并行混合模型预测残差及预测区间如图14所示。

由图14可知，并行混合模型对数据A2具有较高的预测水平，对另外3个数据集的预测效果相对较差，且残差多集中于随机波动较为剧烈的时间段，表明随机波动是影响并行混合模型预测准确率的重要因素之一。数据A1、A3、A4的置信区间在中后期变窄，但此处时间段的残差反而增大，表明模型在此处存在过拟合现象，从而降低模型预测精度。

3" 结" 论

（1）引入添加SENet的MSCNN模型进行滚动轴承退化因子的提取，弥补了传统构建滚动轴承健康曲线时人工干预性强、特征提取不够充分的缺陷，使得滚动轴承RUL预测更为智能化、高效化。

（2）使用并行混合模型对滚动轴承RUL预测缓解了单一模型在变工况下预测鲁棒性不足的问题，同时添加TPA的LSTM机制，强化了对关键时序信息的识别和记忆能力，提高了模型的预测精度。

（3）引入分位数回归用于滚动轴承RUL区间预测，量化了模型预测不确定性，对后续维修决策起到积极作用。通过分析预测区间发现，并行混合模型预测曲线随机波动较大并且在预测中后期存在过拟合的风险，有助于后续模型的改进。

［1］

聂磊，张吕凡，徐诗奕，等．基于相似度特征融合和CNN的滚动轴承剩余寿命预测［J］．噪声与振动控制，2023，43（5）：115-121．

NIE L， ZHANG L F， XU S Y， et al. Remaining life prediction of rolling bearings based on similarity feature fusion and convolutional neural network［J］. Noise and Vibration Control， 2023， 43（5）： 115-121.

［2］" 莫仁鹏，李天梅，司小胜，等．采用残差网络与卷积注意力机制的设备剩余使用寿命预测方法［J］．西安交通大学学报，2022，56（4）：194-202．

MO R P， LI T M， SI X S， et al. Remaining useful life prediction for equipment using residual network and convolutional attention mechanism［J］. Journal of Xian Jiaotong University， 2022， 56（4）： 194-202.

［3］" HOTAIT H， CHIEMENTIN X， RASOLOFONDRAIBE L. Intelligent online monitoring of rolling bearing： diagnosis and prognosis［J］. Entropy， 2021， 23（7）： 791.

［4］" MAREI M， LI W D. Cutting tool prognostics enabled by hybrid CNN-LSTM with transfer learning［J］. The International Journal of Advanced Manufacturing Technology， 2022， 118（3）： 817-836.

［5］" 胡城豪，胡昌华，司小胜，等．基于MSCNN-LSTM的滚动轴承剩余寿命预测方法［J］．中国测试，2020，46（9）：103-110．

HU C H， HU C H， SI X S， et al. Remaining useful lifetime prediction method of rolling bearing based on MSCNN-LSTM［J］. China Measurement amp; Testing Technology， 2020， 46（9）： 103-110.

［6］" WANG F T， LIU X F， DENG G， et al. Remaining life prediction method for rolling bearing based on the long short-term memory network［J］. Neural Processing Letters， 2019， 50（3）： 2437-2454.

［7］" 周圣文，郭顺生，杜百岗．基于LSTM-ES-RVM的滚动轴承剩余寿命预测方法［J］．振动工程学报，2023，36（6）：1723-1735．

ZHOU S W， GUO S S， DU B G. Remaining useful life prediction method of rolling bearing based on LSTM-ES-RVM networks［J］. Journal of Vibration Engineering， 2023， 36（6）： 1723-1735.

［8］" 杜浩飞，张超，李建军．基于SENet-ResNext-LSTM的风机轴承故障诊断［J］．机械强度，2023，45（6）：1271-1279．

DU H F， ZHANG C， LI J J. Fault diagnosis of wind turbine bearing based on SENet-ResNext-LSTM［J］. Journal of Mechanical Strength， 2023， 45（6）： 1271-1279.

［9］" SHIH S Y， SUN F K， LEE H Y. Temporal pattern attention for multivariate time series forecasting［J］. Machine Learning， 2019， 108（8）： 1421-1441.

［10］" AGUSHAKA J O， EZUGWU A E， ABUALIGAH L. Gazelle optimization algorithm： a novel nature-inspired metaheuristic optimizer［J］. Neural Computing and Applications， 2023， 35（5）： 4099-4131.

［11］" WANG B， LEI Y G， LI N P， et al. A hybrid prognostics approach for estimating remaining useful life of rolling element bearings［J］. IEEE Transactions on Reliability， 2020， 69（1）： 401-412.

［12］" 文娟，高宏力．一种基于UPF的轴承剩余寿命预测方法［J］．振动与冲击，2018，37（24）：208-213， 243．

WEN J， GAO H L. Remaining useful life prediction of bearings with the unscented particle filter approach［J］. Journal of Vibration and Shock， 2018， 37（24）： 208-213， 243.

［13］" 刘胜兰，高凌寒，杜剑维，等．基于自适应顺序的滚动轴承最优特征选取与寿命预测［J］．舰船科学技术，2019，41（11）：71-76．

LIU S L， GAO L H， DU J W， et al. Rolling bearing remaining useful life prediction via adaptive sequential optimal feature selection［J］. Ship Science and Technology， 2019， 41（11）： 71-76.

［14］" EAMONN K， SELINA C， DAVID H， et al. Segmenting time series： a survey and novel approach［M］. Singapore： Data Mining in Time Series Databases， 2004： 1-21.

［15］" 李亚平，李素杰，马波，等．基于TCN的滚动轴承振动趋势与剩余寿命预测研究［J］．现代制造工程，2021（9）：124-131．

LI Y P， LI S J， MA B， et al. Research on vibration trend and remaining life prediction of rolling bearings based on TCN［J］. Modern Manufacturing Engineering， 2021（9）： 124-131.

［16］" 李建伟，刘成波，郭宏，等．基于PSO-RBF神经网络的刀具寿命预测［J］．计算机系统应用，2022，31（1）：309-314．

LI J W， LIU C B， GUO H， et al. Tool life prediction based on PSO-RBF neural network［J］. Computer Systems amp; Applications， 2022， 31（1）： 309-314.

［17］" 于永进，姜雅男，李长云．基于鲸鱼优化-长短期记忆网络模型的机-热老化绝缘纸剩余寿命预测方法［J］．电工技术学报，2022，37（12）：3162-3171．

YU Y J， JIANG Y N， LI C Y. Prediction method of insulation paper remaining life with mechanical-thermal synergy based on whale optimization algorithm-long-short term memory model［J］. Transactions of China Electrotechnical Society， 2022， 37（12）： 3162-3171.

［18］" 吴俊伟，陈保家，陈正坤，等．SSA-TCN在涡扇发动机剩余使用寿命预测的应用［J］．三峡大学学报（自然科学版），2023，45（6）：92-100．

WU J W， CHEN B J， CHEN Z K， et al. Application of SSA-TCN in prediction of remaining useful life of turbofan engine［J］. Journal of China Three Gorges University（Natural Sciences）， 2023， 45（6）： 92-100.

第一唐友福，教授，博士研究生导师，生于1981年，2013年毕业于上海大学机械电子工程专业，现从事设备智能运维与健康管理的研究工作。地址：（163318）黑龙江省大庆市。email：tang_youfu210@163.com。

通信作者：李澳。email：2975262616@qq.com。