不同含石量宕渣路基压实特性

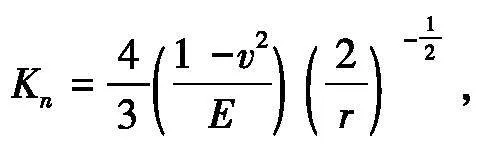
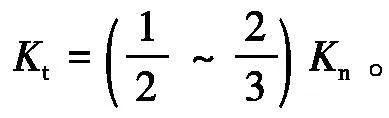
摘要：为研究不同含石量（石在宕渣中的质量分数）宕渣的最佳压实振动频率及动力响应，采用离散元软件EDEM中的接触模型建立多组宕渣路基压实模型，振动频率分别为28、30、34、40 Hz，含石量分别为60%、70%、80%，分析颗粒轨迹、总应力及速度变化等。结果表明：1）含石量分别为60%、70%、80%的宕渣最佳振动频率分别为34、30、40 Hz。2）破碎率随含石量和振动频率的增大而增大；含石量相同时，压实含可破碎颗粒宕渣的孔隙率普遍小于含不可破碎颗粒的宕渣。3）粒径为3、30、70 mm的活跃度分别为0.098、0.716、29.372，粒径为70 mm的大颗粒活跃度较低，粒径为30 mm的颗粒活跃度较高，粒径为3 mm的小颗粒活跃度最高。4）压实过程中，按颗粒平均总应力、颗粒平均速度的变化主要分为塑性压实、工况过渡、压实后期3个阶段。5）在塑性压实阶段时，宕渣颗粒平均总应力较小，以塑性变形为主，振动板和宕渣间的接触力较小；在工况过渡阶段时，振动板与宕渣间的接触力和颗粒平均总应力突变；在压实完成阶段时，宕渣颗粒以弹性变形为主，形成良好的骨架密实结构，颗粒平均总应力较大。6）在塑性压实阶段，颗粒速度不稳定且较低，至压实完成阶段形成骨架密实结构，大、小颗粒相对位置变化较小，大颗粒夹带小颗粒随振动板共同振动，平均速度变化较小。7）颗粒平均速度和平均总应力的阶段性相同，且相同含石量在同一振动频率下的阶段持续时间相同；击实频率接近宕渣固有频率时，颗粒快速达到稳定状态，压实效果最佳。

关键词：宕渣；路基；离散元；击实试验；振动频率;含石量

中图分类号：U416.1文献标志码：A文章编号：1672-0032（2025）01-0043-10

0 引言

宕渣是爆破后产生的粒径大于40 mm、含石量（石在宕渣中的质量分数）大于30%的土石混合料，经级配处理后可做性能良好的路基填料。与填石和填土路基材料相比，宕渣的压实特性比土质或石质路基材料更复杂[1]。颗粒材料的力学性能都受密度影响[2]，压实方法直接影响宕渣的密度。采用离散元方法（discrete element method，DEM）模拟研究宕渣的压实特性及物理力学性能，模拟碎石块体等土结构压实性能简洁高效。

DEM已广泛应用于岩土工程和沥青混合料、级配碎石和细粒土等道路材料等领域[3-5]。Sagnol等[6]评估用于增强沥青结构的玻璃纤维网络对磨损层和黏结层间黏结强度的影响，建立基于有限元模拟的数值模型，采用材料的颗粒粒径分布创建数值样品，此数值模型能较好地再现沥青混合料和加筋沥青混合料在剪切荷载下的力学行为。Jia等[7]通过建立离散元仿真模型，研究颗粒在动态压实过程中的宏观和微观机制，揭示颗粒动态压实的两个阶段，即瞬态冲击引起的压实和振动压实。Ji等[8] 基于DEM和计算机层析图像（computerized tomography，CT）扫描提出土石混合料振动压实方法的数值模拟方法，建立最大粒径大于40 mm的土石混合料最大干密度的预测模型，与实际测量结果对比，结果表明预测模型的预测精度较高，最大干密度随最大粒径和巨粒用量的增大而增大，土石比合适时，土石混合料才能形成较好的骨架致密结构。方磊等[9]采用随机离散单元法建立石料颗粒的结构模型，模拟填石路基振动压路机施工过程中碾压压力、振动频率、激振力条、碾压遍数等因素对填石路基压实效果的影响，结果表明，振动能量与振动频率对填石路基的压实效果有最佳组合，振动压路机的碾压遍数与振动频率有一定关系。黄宝涛等[10]采用二维离散元法分析振动压实下不规则颗粒体的细观响应，发现颗粒间存在相对竖向位移和侧向位移，且沿轴对称线大致对称分布。王强等[11]结合室内大型击实试验和数值模拟，研究不同块石质量分数和不同岩石形状的软岩土石混合体的击实特性和细观机理。Karrech等[12]建立三维离散元模型，采用模拟长期循环荷载作用下三维颗粒响应的计算方法，采用分子动力学、时间平均技术和松弛法预测颗粒材料的长期流动。

颗粒破碎对宕渣压实效果的影响不可忽视。含石量较大的宕渣体积收缩，原因是初始孔隙压缩和岩石块破裂导致级配和结构调整 [13-14]。丁智勇等[15]采用软件EDEM建立正方体、三棱体、球体3种可破碎颗粒和刚性颗粒的路基压实模型，分析压路机频率及激振力对填石路基压实的影响，证明含可破碎填料的填石路基压实离散元法模拟结果准确可靠。已有研究集中于振动频率及含石量对土石混合料击实效果的影响，对不同含石量混合料的最佳压实振动频率的研究较少。离散元数值模拟可较好地模拟碎石块体等土结构压实，但建立模型时大多未考虑颗粒破碎对压实效果的影响。

本文采用离散元软件中的Hertz-Mindlin（no slip）接触模型建立可破碎宕渣颗粒离散元路基模型，研究不同含石量宕渣在不同振动频率下的单个颗粒轨迹、颗粒平均总应力和颗粒平均速度的变化规律，为宕渣压实过程中振动压路机振动频率的选择提供参考依据。

1 试验材料

选用济潍高速公路路堑开挖产生的宕渣作为土石混合料，原始粒径为0～80 mm，宕渣岩性为石灰岩。

根据最大密度曲线n幂公式得到宕渣级配 [16]，某粒径宕渣的通过率

p=100（d/D）n，

式中：d为某级配宕渣的粒径，D为宕渣的最大粒径。

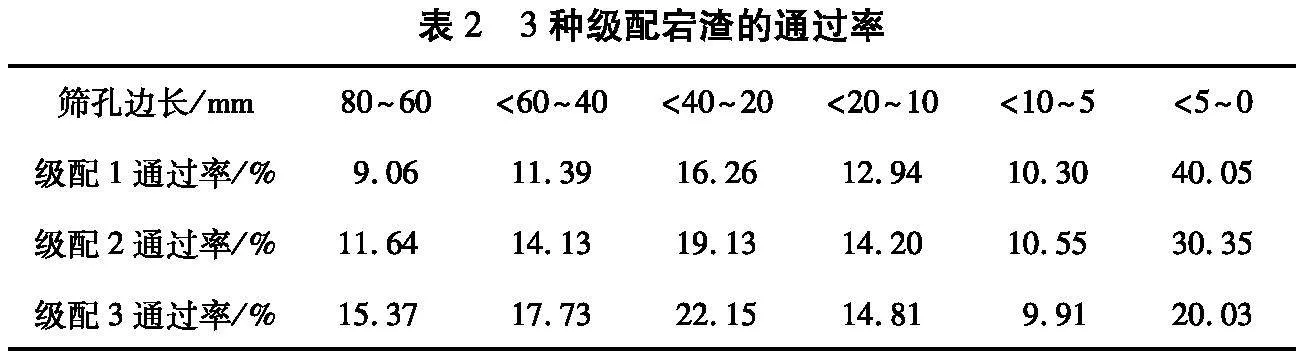
选用3种不同级配的宕渣，综合考虑粒径小于5 mm的粒料在宕渣中的质量分数w5、曲率系数Cc及不均匀系数Cu，如表1所示，3种级配宕渣通过率如表2所示。

2 振动击实仿真模型

为提高计算效率，保证宕渣的压实特性和总质量均不变，将半径小于1.5 mm的颗粒换算为半径1.5 mm的颗粒，设置不可破碎颗粒为球形，可破碎颗粒为方形[17]。

2.1 仿真参数确定

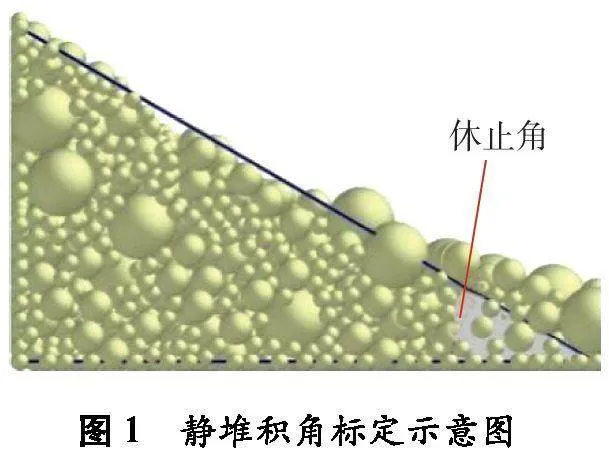
石灰岩和钢的泊松比分别为0.2、0.3，剪切模量分别为20、70 GPa，密度分别为2 690、7 800 kg/m3[18]。依靠标定试验确定基本参数模型，采用静堆积角试验标定颗粒-颗粒和颗粒-试筒的接触参数，静堆积角标定示意图如图1所示。

依次标定恢复系数、静摩擦因数、滚动摩擦因数等接触参数，记录土石混合料塌落后的角度，休止角为37.1°时，颗粒-颗粒和颗粒-几何体的恢复系数分别为0.15、0.20，静摩擦因数分别为0.3、0.5，滚动摩擦因数分别为0.05、0.01。

宕渣颗粒的抗压强度和刚度相对较高，路基中的宕渣表现为线弹性，选用Hertz-Mindlin（no slip）模型为接触模型，如图2所示。

2.2 可破碎颗粒生成

采用软件EDEM生成若干大粒径颗粒，在特定时刻采用颗粒体积力移除大粒径颗粒，用小颗粒群填充空间位置，通过颗粒黏结插件粘接小颗粒，形成具有一定抗压抗拉强度和形状的可破碎岩石颗粒，替代原来的大粒径颗粒，颗粒替换示意图如图3所示[15]。

依靠替换后小颗粒间的黏结力体现岩石强度，黏结力由Kn、Kt 、最大正应力σmax、最大切应力τmax表征，黏结半径一般为小颗粒粒径的1/2[18]，法向接触刚度系数

式中：v为泊松比，E为岩石弹性模量，r为Friction小颗粒半径。

切向接触刚度系数

最大切应力

τmax=C+σmaxtan φ ，

式中C为内聚力。

试验用岩石颗粒的Kn=2.635×109 N·m-3， K t=1.318×109 N·m-3，σmax=245 MPa，

τmax=101 MPa，黏结半径为2 mm。

自制击实试筒如图4a）所示，进行室内振动击实试验后宕渣如图4b）所示，不同含石量宕渣在不同振动频率f下击实后的破碎率如表3所示。

根据表3结果设置可破碎颗粒在大颗粒中的质量分数，宕渣含石量分别为60%、70%、80%时，可破碎颗粒质量分数分别为29%、32%、35%。

2.3 EDEM振动击实模型建立

根据宕渣颗粒实际粒径，综合考虑压路机实际压实工况及宕渣颗粒尺寸效应，根据土石混合料相关施工经验及文献确定振动击实模型[18]。

建立路基模型，采用加载板模拟压路机压实过程，假定振动轮与路基表面为条形接触，输入简谐振动方程控制振动板完成振动加载。为保证施工质量，路基压实设备多选用工作质量大于18 t的大激振力设备，在压实模拟中参考压路机LSS218A的性能参数，设置模拟振动参数如表4所示。

宕渣颗粒最大粒径一般为松铺厚度的 1/3～2/3 ，仿真试验中最大粒径为 80 mm，因此路基松铺厚度为240 mm 较佳。根据压路机的设计原理[19]，接地宽度

B=（D1/2）sin A，（1）

式中：D1 为轮的直径，D1=1.6 m；A为振动轮阻角，取A=8.836{B}，其中{B}为以m为单位的B的数值。

对式（1）进行泰勒近似替代，计算得到B=0.308 m。为节约计算成本，取压路机接地长度的1/2作为仿真压路机接地长度，为1.065 m。综合考虑颗粒最大半径及压路机接地宽度，地基模型宽度取5倍最大粒径宽度，设置路基模型区域的长、宽、高分别为1.2、0.4、0.4 m，将半正弦波加载到振动板上，振动板置于宕渣上。施加荷载

F=-∣Wz+F0sin（2πft）∣，

式中：Wz为振动板与振动电机自质量，F0为激振力，f为振动频率，t为仿真运行时间。

设Wz=45 kN，固定激振力F0=110 kN，分别设置振动频率为28、30、34、40 Hz。

时间步长足够小可保证模拟系统的稳定性。通常将瑞利时间步长视为准静态颗粒收集DEM模拟的理论最大时间步长。固定时间步长为瑞利时间步长的20%～40%时较合适[20]，此处设置时间步长为20%。

设置6组击实模型，其中3组模型含可破碎颗粒，3组模型不含可破碎颗粒。因离散元模拟的局限性，只能通过空隙率直观体现压实状态。采用最终稳定孔隙率作为模拟试验的控制指标，根据施工经验设置振动压实仿真运行18 s[17]。

3 模拟结果分析与讨论

3.1 压实度变化

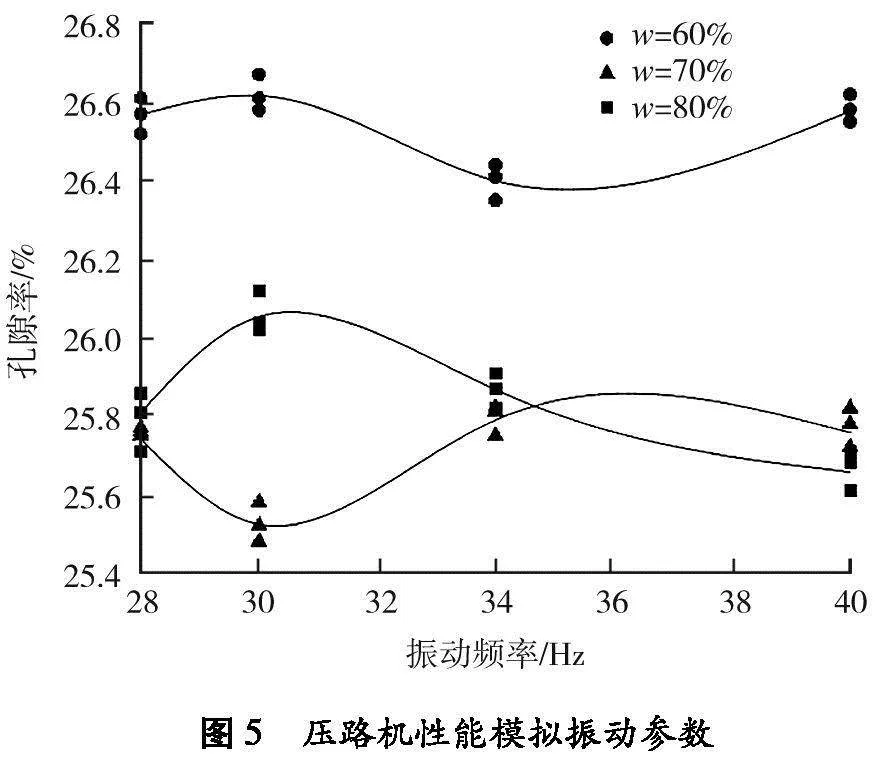
在宕渣模型振动板下创建3个区域进行孔隙率检测，压实完成后，比较不同含石量w的宕渣在不同振动频率下的孔隙率。振动频率与最终孔隙率的关系如图5所示。由图5可知：含石量分别为60%、70%、80%时，达到宕渣最佳压实效果的最佳振动频率分别为34、30、40 Hz。

3.2 破碎率对压实效果的影响

将黏结键断裂作为颗粒破损的表征形式，通过断裂键数获得破碎率指标，不同含石量宕渣在不同振动频率下的破碎率量化指标如表5所示。

由表5可知：破碎率随含石量和振动频率的增大而增大。原因是随含石量的增大，细颗粒逐渐减少，大颗粒间孔隙未被完全填满，大颗粒骨架出现应力集中，更多的颗粒破碎。

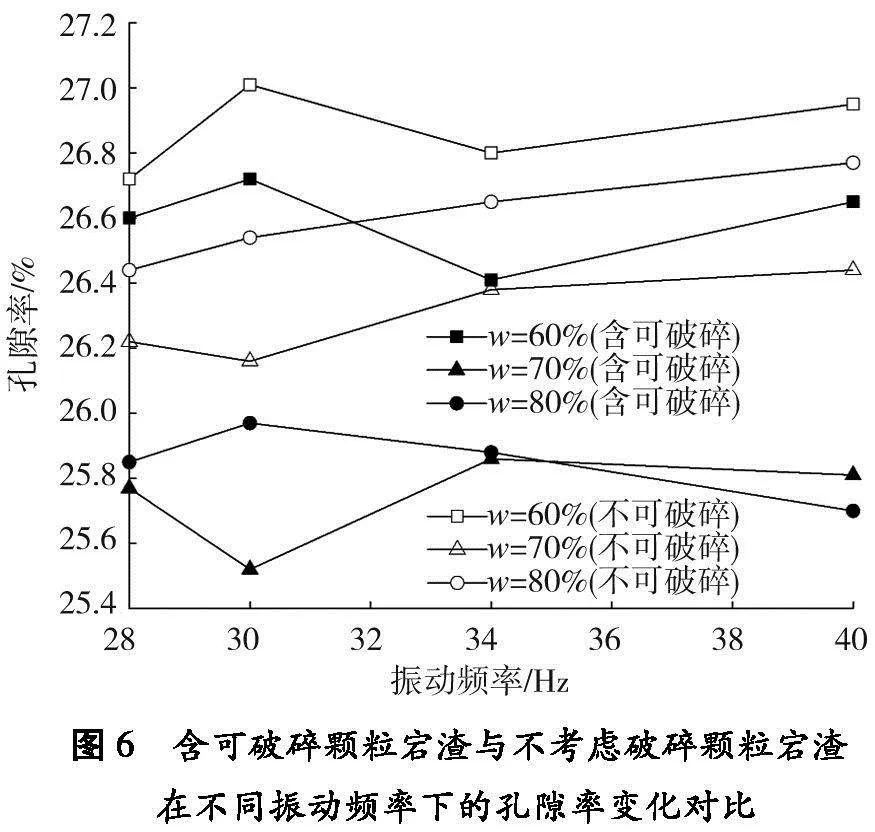
为探究颗粒破碎对压实效果的影响，在不同振动频率和含石量w下，将含可破碎颗粒宕渣与不考虑破碎颗粒宕渣的压实效果对比，结果如图6所示。

由图6可知：不考虑宕渣颗粒破碎时，含石量分别为60%、70%、80%的土石混合料达到最佳压实效果的振动频率分别为34、30、28 Hz，含石量越大的宕渣达到最佳压实效果的振动频率越小。颗粒破碎对含石量为60%宕渣的影响较小；含石量为60%、70%时，含可破碎和不可破碎的宕渣达到最佳压实效果时的振动频率相同；含石量为80%时，含可破碎和不可破碎的宕渣分别在振动频率为40、28 Hz时达到最佳压实效果。

含石量相同时，压实含可破碎颗粒宕渣后的孔隙率普遍小于含不可破碎颗粒的宕渣，原因是含石量为50%～70%时[21]，石颗粒间完全被土颗粒填充，且石颗粒相距较近，形成骨架密实结构，达到最大密度，此时为最佳含石量范围。含石量为60%的宕渣破碎对压实度无较大影响，原因是大颗粒周围被小颗粒充实，应力被削弱分散，大颗粒破碎量较少，且此时处于最佳含石量范围。含石量大于70％时，石颗粒间空隙未被土颗粒完全填充，形成残余空隙，且空隙随含石量的增大而增大，密度相对较小。颗粒破碎造成大颗粒减少，小颗粒增多，当宕渣含石量大于最佳含石量时，破碎后的宕渣含石量更接近最佳含石量，则破碎有利于提高压实度。振动频率越大，破碎率越大，振动频率为40 Hz时宕渣的破碎率最大，含石量为80%的宕渣达到最小孔隙率。

3.3 单个颗粒运动轨迹

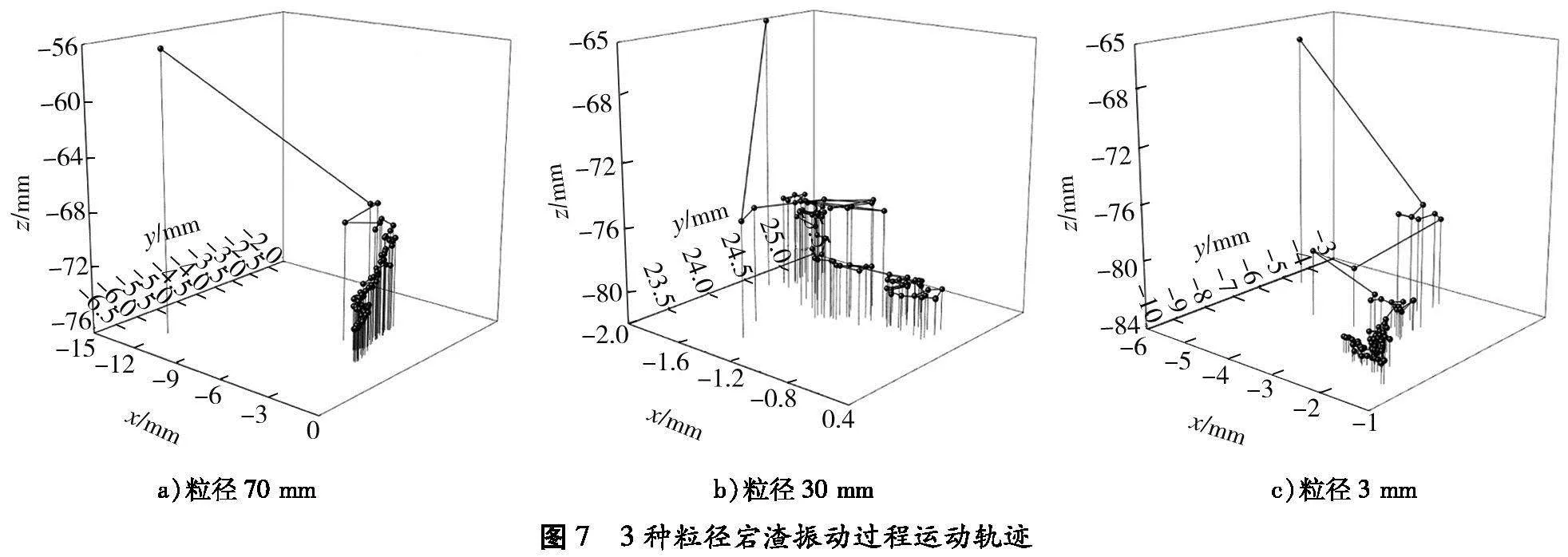
分析含石量为70%的宕渣颗粒的运动轨迹，在振动板下方选择粒径为3、30、70 mm的颗粒，绘制运动轨迹，结果如图7所示。

由图7可知：不同粒径宕渣的运动轨迹差异明显。为更直观展示颗粒的运动状况，引入颗粒活跃度的概念，采用颗粒在x、y、z轴活动的最大范围、粒径和颗粒速度体现颗粒活跃度a，计算公式为：

a=Xmax-XxinYmax-YxinZmax-Zxinv/D2 ，（2）

式中：Xmax、Xmin分别为颗粒在x轴方向运动的最大位移和最小位移；Ymax 、Ymin分别为颗粒在y轴方向运动最大位移和最小位移；Zmax 、Zmin分别为颗粒在z轴方向运动最大位移和最小位移；v为颗粒平均速度，m·s-1；D2为颗粒粒径，mm。

根据式（2）计算3种粒径为3、30、70 mm颗粒的活跃度，分别为29.372、0.716、0.098。

粒径为3 mm时颗粒活跃度最大，原因是振动板连续振动压实带动小颗粒运动，小颗粒充分填充空隙；粒径为70 mm时颗粒活跃度最小，运动轨迹单一，原因是大颗粒起到宕渣主要骨架的作用，形成受力骨架后大颗粒相互作用，限制运动。

3.4 颗粒平均总应力

压实宕渣过程中，总应力的变化可较好地表征宕渣的压实机理[11]。振动频率分别为28、30、34、40 Hz时，采用加载板对含石量分别为60%、70%、80%的宕渣加载18 s，3种含石量宕渣在4种振动频率作用下平均总应力随时间的变化如图8所示。

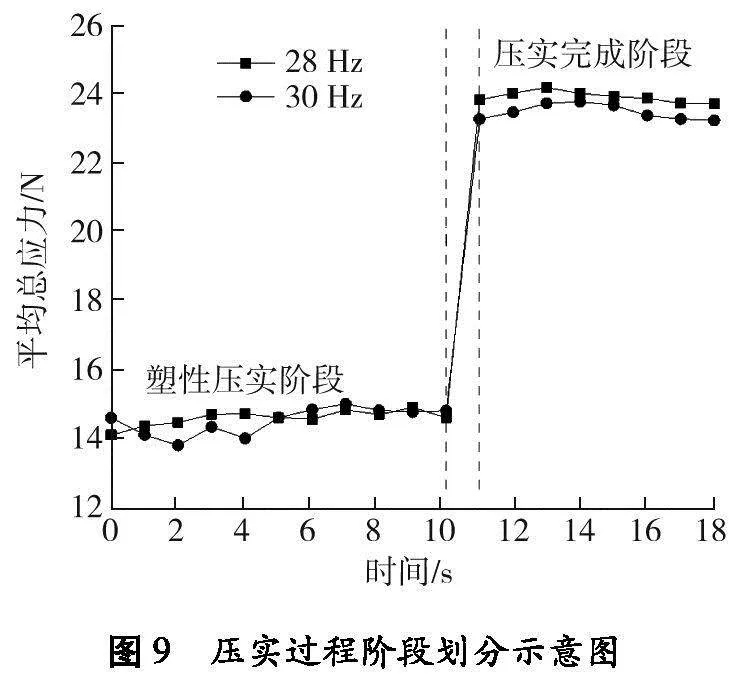
压实过程中，按平均总应力的变化主要分为塑性压实、工况过渡、压实完成3个阶段，阶段划分如图9所示。

由图8、9可知：处于塑性压实阶段时，宕渣颗粒平均总应力较小，以塑性变形为主，振动板和宕渣间的接触力较小；在工况过渡阶段时，振动板与宕渣间的接触力和颗粒平均总应力突变；在压实完成阶段时，宕渣由以塑性变形为主转变为以弹性变形为主，宕渣已形成良好的骨架密实结构，颗粒平均总应力较大[22]。

振动频率为34 Hz时，击实含石量为60%的宕渣，与振动频率为28 Hz 时，击实含石量为80%的宕渣，3个压实过程阶段变化不明显，全程平均总应力较大但变化较小，说明振动板和宕渣产生共振效应，颗粒获得较大能量，土颗粒由静态过渡为动态，此时宕渣处于液化形态[23]，内摩擦阻力急剧减小，在外力作用下，宕渣颗粒易向低位能方向流动，相互填充楔紧，快速增大土石混合料的密实度，迅速达到紧密受力结构。

不同含石量下宕渣的固有频率不同。根据共振压实原理[24]可推出，振动频率为34 Hz时接近含石量为60%的宕渣的固有频率，振动频率为28 Hz时接近含石量为80%的宕渣的固有频率。含石量为70%的宕渣未出现这种情况，原因可能是试验所用振动频率未与含石量为70%的宕渣产生共振效应。

在相同振动频率下，3种含石量宕渣在塑性压实阶段的持续时间不完全相同，说明不同含石量宕渣对相同振动频率的反应不同。压实完成后，压实效果越好，平均总应力越大，说明颗粒平均总应力与密实度的关联性较强。可把到达压实后期的时刻作为最终压实的时刻。

3.5 颗粒平均速度

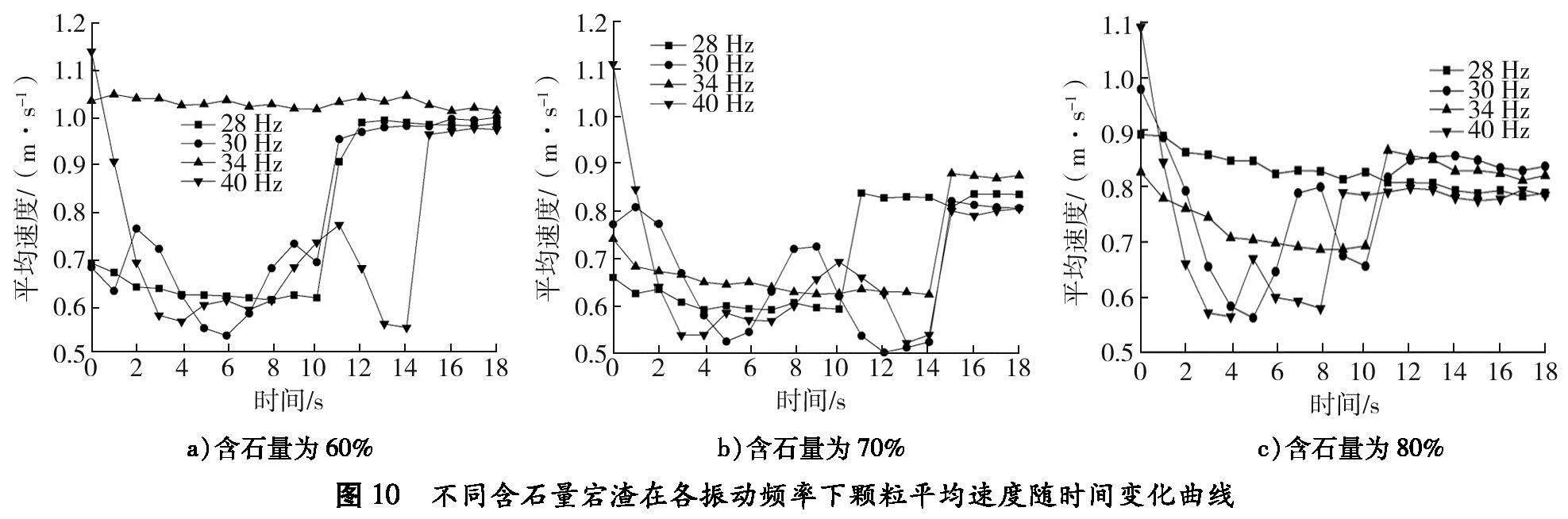
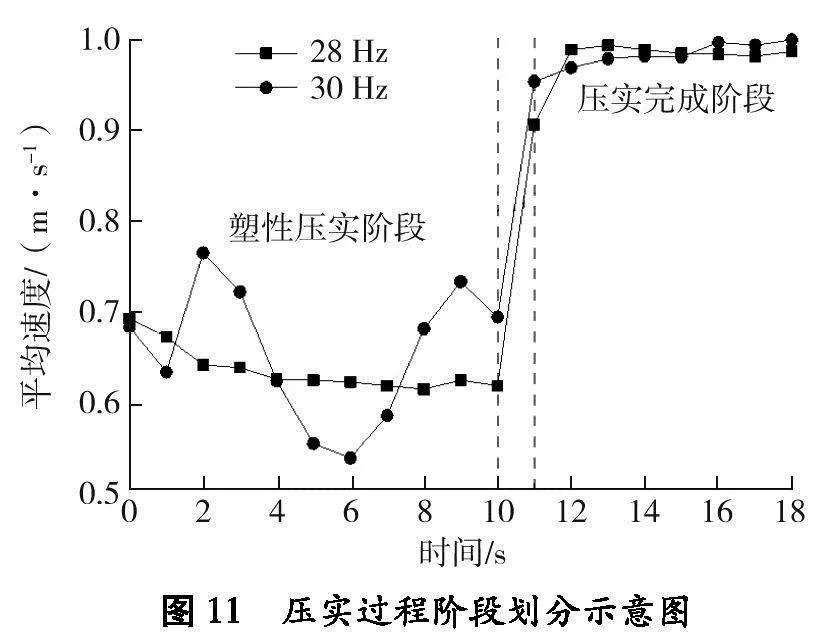
振动过程中，颗粒速度的变化反映宕渣在压实过程中的运动状态，可分析宕渣的压实状态。分析不同含石量下宕渣颗粒的平均速度，绘制颗粒平均速度随时间变化曲线，如图10所示。压实过程阶段划分如图11所示。

由图10、11可知：压实过程中，按颗粒平均速度的变化可分为塑性压实、工况过渡和压实完成3个阶段。在塑性压实阶段，振动频率为30 Hz时，颗粒平均速度不稳定且总体处于较低水平，原因是宕渣较松散，随振动板连续振动压实，宕渣结构为骨架密实结构，打破已形成密实结构的反复压实状态。经过工况过渡阶段到达压实完成阶段，宕渣内部形成骨架密实结构，大、小颗粒的相对位置不会发生较大改变，大颗粒夹带小颗粒随振动板共同振动，颗粒平均速度变化较小。

含石量为60%的宕渣在振动频率34 Hz下，以及含石量为80%的宕渣在振动频率28 Hz下击实时，颗粒平均速度未发生阶段性变化，这是因为振动板和宕渣产生共振效应，宕渣迅速达到密实结构。

3.6 可破碎宕渣压实效果与颗粒活跃度、平均总应力及平均速度关联性

颗粒平均速度和平均总应力存在相同的阶段性，且相同含石量在同一振动频率下的阶段持续时间相同。宕渣处于塑性压实阶段时，较大粒径颗粒随振动板上下运动，中粒径颗粒做小范围竖向运动和小幅水平摇摆，小颗粒能做任意方向的不规则运动，填充石块颗粒孔隙。这时宕渣处于不密实状态，大颗粒不能较好地夹带小颗粒运动，颗粒间的接触点较少，平均总应力处于较低水平，小颗粒受激振力影响较小，颗粒平均速度较小。到达压实后期，宕渣内部形成紧密结构，颗粒间接触点数较多，颗粒的相对位置不发生较大改变，宕渣对激振力的响应增强，大颗粒夹带小颗粒随振动板一起移动，颗粒平均速度和平均总应力增大。

在击实频率接近宕渣固有频率时，达到最佳颗粒压实效果[25]，含石量为80%的宕渣固有振动频率约为28 Hz，如果不考虑颗粒破碎带来的影响，如图8所示，此含石量宕渣在振动频率为28 Hz时达到最佳压实效果，而考虑颗粒破碎的宕渣未在振动频率为28 Hz时达到最小孔隙率，这是因为含石量80%大于最佳含石量，颗粒破碎为土颗粒，含石量减小，接近最佳含石量，土颗粒可填充骨架缝隙，宕渣内部形成更稳定的骨架结构，宕渣更密实，含石量为80%的宕渣在破碎率最大的振动频率40 Hz下达到最佳压实效果。参考宕渣的固有频率，采取相应的振动频率使宕渣达到最佳压实效果，且考虑颗粒破碎带来的影响。

4 结论

建立宕渣路基振动击实的离散元仿真模型，对不同含石量和破碎率的宕渣在不同击实频率的击实过程进行仿真分析，得到击实后的孔隙率、不同粒径颗粒的运动规律、颗粒平均总应力和颗粒平均速度的变化规律以及颗粒破碎对振动击实效果的影响规律。

1）含石量为60%、70%、80%的宕渣达到最佳压实效果的振动频率分别为34、30、40 Hz。

2）含石量相同时，振动频率越大，宕渣破碎率越大；振动频率相同时，含石量越大，宕渣破碎率越大。含石量较大的宕渣破碎率越大，压实效果越好;含石量较小的宕渣破碎率越大，压实效果越差。

3）压实过程中，粒径为70 mm的大粒径颗粒活跃度较低，运动轨迹较单调，多为竖直方向的运动；粒径为30 mm的中粒径颗粒轨迹相对活跃，为小幅度多方向运动；粒径为3 mm的小粒径颗粒活跃度最高，为大幅度多向不规则运动。

4）整个压实过程分为塑性压实、工况过渡、压实完成3个阶段。宕渣颗粒平均总应力与压实度有密切联系，在压实后期平均总应力越大，宕渣越密实，压实过程有明显的工况过渡阶段，此阶段宕渣的压实度显著提高。振动板的振动频率接近宕渣固有频率时，宕渣快速达到密实状态。

参考文献：

[1] 金磊，曾亚武，张森. 块石含量及形状对胶结土石混合体力学性能影响的大型三轴试验[J].岩土力学， 2017， 38（1）：141-149.

[2] XU W J， ZHANG H Y. Research status anddevelopment trend of soil-rock mixture[J].Advances in Science and Technology of Water Resources， 2013， 33（1）：80-88.

[3] CUNDALL P A. A computer model for simulating progressing large-scale movements in blockyrock systems[C]//Proceedings of the Symposium of the International. Rotterdam：A. A Balkema， 1971， 1：8-12.

[4] CUNDALL P A， STRACK O D L. A discrete numerical model for granular assemblies[J].Geotechnique， 1979，29（1）：47-65.

[5] HU S Y， HAN D D， FENG G M， et al. Influence of stress on void ratios of compacted crushed rock masses in coal mine gobs[J].Natural Resources Research， 2020， 29（2）：1361-1374.

[6] SAGNOL L， QUEZADA J C， CHAZALLON C， et al. Effect of glass fibre grids on the bonding strength between two asphalt layers and its contact dynamics method modelling[J].Road Materials and Pavement Design：an International Journal， 2019， 20（5/6）：1164-1181.

[7] JIA M， YANG Y， LIU B， et al. PFC/flac coupled simulation of dynamic compaction in granular particles[J].Granular Matter，2018，20（4）：76.

[8] JI X P， HAN B， HU J M， et al. Application of the discrete element method and CT scanning to investigate the compaction characteristics of the soil-rock mixture in the subgrade[J].Road Materials and Pavement Design：An International Journal， 2022， 23（1/3）：397-413.

[9] 方磊，姜在田，项伟圆.影响填石路堤压实施工因素的数值模拟[J].南京大学学报（自然科学版），2005（6）：658-663.

[10] 黄宝涛，张敏思，雍军.振动压实下不规则颗粒细观响应的离散元模拟[J].公路交通科技，2009，26（7）：7-12.

[11] 王强， 胡新丽， 徐迎， 等. 软岩土石混合体的击实特性与细观机理研究[J].浙江大学学报 （工学版）， 2018， 52（12）：2295-2305.

[12] KARRECH A， DUHAMEL D， BONNET G， et al. A computational procedure for the prediction of settlementingranular materials under cyclic loading[J].Computer Methods in Applied Mechanics and Engineering， 2007， 197（1/2/3/4）：80-94.

[13] WANG J J，ZHANG H P， DENG D P，et al. Effects of mudstone particle content on compaction behaveior and particle crushing of a crushed sandstonemudstone particle mixture[J].Engineering Geology， 2013，167：1-5.

[14] 乔兰， 庞林祥， 李远，等. 超大粒径人工砾石土的击实特性试验研究[J].岩石力学与工程学报， 2014， 33（3）：484-492.

[15] 丁智勇，李国政，张通化，等.含可破碎填料的填石路基压实仿真[J].筑路机械与施工机械化，2019，36（11）：56-61.

[16] 董云. 土石混合料力学特性的试验研究[D].重庆：重庆交通学院，2005.

[17] 王团结. 基于三维离散元的土石混合料振动压实特性研究[D].郑州：郑州大学，2015.

[18] 张通化. 填石路基振动压实过程离散元仿真研究[D].西安：长安大学，2018.

[19] 杨士敏，傅香如.工程机械地面力学与作业理论[M].西安：人民交通出版社，2010.

[20] MIAO Y， YU W， HOU Y， et al. Investigating the functions of particles in packed aggregate blend using a discrete element method[J].Materials， 2019，12（4）：12040556.

[21] 邹海味，熊越，陈学军.土石混合料的压实与力学性能研究[J].公路，2019，64（6）：32-38.

[22] PAULMICHL I， FURTMLLER T， ADAM C， et al. Numerical simulation of the compaction effect and the dynamic response of an oscillation roller based on a hypoplastic soil model[J].Soil Dynamics and Earthquake Engineering， 2020， 132：106057.

[23] 闫从军.填石路基压实试验与作业质量控制研究[D].西安：长安大学，2004.

[24] 程晓明. 土石混填路基压实特性与数值模拟[D].西安：长安大学，2012.

[25] WERSLL C， NORDFELT I， LARSSON S. Resonant roller compaction of gravel in full-scale tests[J].Transportation Geotechnics， 2018， 14：93-97.

Compaction characteristics of slag subgrade with different rock content

Abstract：To study the optimal compaction vibration frequency and dynamic response of different stone content in tailings slag， multiple compaction models for tailings roadbed are established using the contact model in the discrete element software EDEM. The vibration frequencies are set at 28， 30， 34， and 40 Hz， with stone contents of 60%， 70%， and 80%. The analysis focuses on particle trajectories， total stress， and velocity variations. The results indicate that：1） The optimal vibration frequencies for tailings slag with stone contents of 60%， 70%， and 80% are 34， 30， and 40 Hz， respectively.2） The crushing rate increases with the rise of stone content and vibration frequency; for the same stone content， the porosity of the compacted mixtures containing crushable particles is generally lower than that of the mixtures containing non-crushable particles.3） The activity of particles with sizes of 3， 30， and 70 mm is 0.098， 0.716， and 29.372， respectively;the activity of larger particles （70 mm） is lower， while the activity of medium-sized particles （30 mm） is higher， and the smallest particles （3 mm） have the highest activity.4） During the compaction process， based on the changes in average total stress and average particle velocity， the process is mainly divided into three stages：plastic compaction， working condition transition， and completion of compaction.5） In the plastic compaction stage， the average total stress of tailings particles is low， predominantly undergoing plastic deformation， with small contact forces between the vibration plate and the tailings; during the working condition transition stage， there is a sudden change in contact forces between the vibration plate and tailings， as well as in the average total stress of the particles; in the completion stage， tailings particles underwent primarily elastic deformation， forming a well-structured dense skeleton with a higher average total stress.6） In the plastic compaction stage， the particle velocity is unstable and low， while in the completion stage， a dense skeletal structure is formed， with little variation in the relative positions of large and small particles；large particles carry small particles and vibrate together with the vibration plate， resulting in minor changes in average velocity.7） The phases of average particle velocity and average total stress are consistent， and for the same stone content at the same vibration frequency， the duration of the phases is the same;when the impact frequency approached the inherent frequency of the slag， the particles quickly reach a stable state， resulting in the best compaction effect.

Keywords： slag; subgrade; discrete element; compaction test; vibration frequency; stone content