相关变换及其在车窗纹波周期估计中的应用

【摘" 要】本文针对车窗电机纹波周期估计提出一种新方法——相关变换法。经过相关变换后的输出信号与输入信号具有相同周期，且相关变换后输出信号的基波与各次谐波初始相位均为0，这使得在相关变换后输出信号的基波上峰点及邻域范围内，因谐波的同相叠加，基波的上峰锐度和信噪比得到显著增强。在相关变换输出域进行信号周期估计时，其准确性和可靠度能够大幅提升。文章对相关变换的优良特性进行理论证明、仿真验证以及实例验证，结果准确无误。

【关键词】有刷电机；相关变换；纹波；周期估计；车窗；防夹

中图分类号：U463.85"""" 文献标识码：A""" 文章编号：1003-8639（2025）01-0065-07

Correlation Transformation and Its Application in Estimation of Window Ripple Period

CHEN Guoan，LIU Donghui，GU Hongtao，FU Zhaohui

（Geely Automobile Research Institute，Ningbo 315336，China）

【Abstract】In this paper，a new method for estimation of ripple period of window motor，the correlation transform method，is proposed. The output signal after correlation transformation has the same period as the input signal，and the initial phase of the fundamental wave and each harmonic of the output signal after correlation transformation is zero. Due to the in-phase superposition of harmonics，the peak sharpness and signal-to-noise ratio of the fundamental wave are significantly enhanced in the range of the fundamental peak point and neighborhood of the output signal after the correlation transformation. The accuracy and reliability of the signal period estimation in the output domain of the correlation transform can be greatly improved. In this paper，the excellent characteristics of correlation transformation are proved by theory，simulation and example，and the results are accurate.

【Key words】brush motor；correlation transformation；ripple；cycle estimation；car windows；anti-pinch

国标GB11552—2009[1]要求电动车窗须具备防夹功能，该标准第4.8.3“自动回缩要求”一节中规定车窗玻璃上距边缘4～200mm范围内须具备防夹回缩功能。文献[2]对电动车窗防夹技术做了全面的介绍。近年来，采用有刷电机电流纹波信号取代霍尔信号进行车窗玻璃定位与防夹被广泛研究[3-6]，其中，电机的纹波周期估计与周期分割是定位（纹波计数）与测速（周期分割）的关键。特别是在低温重载极端环境下，纹波畸变严重，纹波周期估计与分割的准确性和可靠性成为考验控制器性能的关键指标。

电机纹波周期估计在应用于运行控制时，由于实时性要求，必须在短时间内完成。直接对纹波时域波形进行整形和边沿检测是常用方法。然而，经长期使用磨损或制造过程中存在轻度缺陷的电机，在低温和重负载时电机纹波波形变形严重。其纹波相邻周期的电流存在跌落/跃升现象，一个纹波周期内波形可能出现严重的M波（波形下凹）。而纹波整形的判决线是缓变的，这会造成部分周期纹波的判决线偏上或偏下，导致整形脉冲边沿大幅抖动，甚至存在个别纹波整个周期位于判决线之上/之下，从而导致纹波漏检（纹波计数少计），或者个别M波深度低于判决线，导致纹波多检（纹波计数多计），进而造成整体定位误差超标（防夹区定位不准），功能偶发失常（车窗不防夹和误防夹）。

本文提出一种信号相关变换方法，并将其应用于有刷电机纹波周期估计中，可显著提高控制器对纹波畸变的容忍度，使得纹波周期估计的准确性和稳定性得到较大幅度提升。

1" 信号相关运算及三角函数整周期相关运算

的特性

1.1" 相关运算

依据图1示例说明两信号采样序列的相关运算过程。

图1中，[Ai （i=0，…，19）]是相关运算的输入序列，[Bj （j=0，…，4）]是相关运算的本地序列，[Ck （k=0，…，15）]是相关运算的输出序列，其每个输出值如下。

[C0=A0⋅B0+A1⋅B1+A2⋅B2+A3⋅B3+A4⋅B4]

[C1=A1⋅B0+A2⋅B1+A3⋅B2+A4⋅B3+A5⋅B4]

[C2=A2⋅B0+A3⋅B1+A4⋅B2+A5⋅B3+A6⋅B4]

…" …" …

[C15=A15⋅B0+A16⋅B1+A17⋅B2+A18⋅B3+A19⋅B4]

相关运算输出序列[Ck]的通用表达式为：

[Ck=Ak+0⋅B0+Ak+1⋅B1+Ak+2⋅B2+Ak+3⋅B3+Ak+4⋅B4]

更一般性的，相关运算输出可表示如下：

[Ck= j=0（N−1）Ak+j⋅Bj ]

式中：[Ai ]——相关运算输入信号序列；[Bj ]——相关运算的本地序列；[Ck ]——相关运算输出序列；[N]——本地序列[Bj]的长度。

1.2" 三角函数及其谐波整周期相关运算及其性质

三角函数积化和差公式为：

[cosx ⋅cosy= 12[cos（x+y）+cosx−y]]

设[x（t）=cosω1t+θ1，" y（t）=cosω2t+θ2]，[st ]是[x（t）]与[y（t）]的乘积，有：

[st=cosω1t+θ1 ⋅cosω2t+θ2=12 {cos[（ω1+ω2）⋅t+θ1+θ2]+cos[（ω1−ω2）⋅t+θ1−θ2]}]

如果两信号的频率成位数关系，即[ω2=][n⋅ω1]，这里[n]是正整数，即[f2=ω22π] = [n⋅ω12π=n⋅f1]，即[y（t）]是基波[x（t）]的[n]次谐波。

三角函数及其谐波的整周期相关运算，输出用[ct]表示，[T1=1f1]是基波的周期，[st]在基波周期[[0，T1]]上的定积分为[ct] ，则

式中：[c1t]——[st]积分后的“和频”项；[c2t]——[st]积分后的“差频”项。

[+ω2）⋅t+θ1+θ2]dt]，进一步，区分[n≠1]和 [n=1]两种情况。

1）当[n≠1]，即[ω2≠ω1]时，[c1t]和[c2t]展开推导如下：

将[ω2=n⋅ω1]代入，有

将[ω2=n⋅ω1] 代入，有

以上推导过程中，利用了等式关系：（[f1⋅T1）=（1T1⋅T1）=1]，以及[sink⋅2π+θ=sin（θ）] ，其中[k]为整数。值得注意的是，[c1t ]与[c2t] 为0的结果与[θ1]、[θ2]的取值无关。所以在[ω2≠ω1]情况下，[ct=12c1t+c2t =0 。]

2）当 [n=1]，也就是[ω2=ω1] 时，此时[c1t]的推导过程与[n≠1]时的情况相同，仍然有[c1t=0]。但[c2t]的推导过程，因为[（ω1−ω2）]=0不能为分母，重新推导如下。

当[θ2=θ1]时，[c2t=][T1][⋅][cos（0）][=T1]，[ct]取得最大值[12⋅T1]。所以，在[ω2=ω1]情况下，[ct=12⋅T1⋅cosθ1−θ2=12⋅T1⋅cosΔθ 。]

上述理论推导是在模拟域以定积分形式进行的，在采样后的数字域，对应的是时域波形进行相关运算，积分长度是该余弦信号的1个周期；对于整数倍M周期内的定积分可看作是M个单周期的积分之和。

由上述可见，对于整周期定积分或采样后的相关运算，输入信号与本地信号，无论是余弦信号或者是其任意次谐波，只要二者的频率不同，则该时域波形相关运算的输出恒为0，此结论与输入信号与本地信号的初始相位及二者的相位差无关；如果输入信号与本地信号的频率相同，则该时域波形相关运算的输出序列是二者相位差的余弦值。尤其当输入信号与本地信号频率相同时，本地信号保持起始时的序列固定不变，输入信号在一个周期[[0，T1）]内滑动，二者之间的相位差相应经历[θ∈[0，2nπ）]（[n]为谐波次数），则二者相关变换的输出波形是一个初始相位为0的完整的[n]次余弦波。

2" 信号相关变换及电机纹波相关变换的特性

2.1" 电机纹波信号波形的数学表示

电机纹波波形[xRipplet] 可表示为：

式中：[x18t， x14t， x12t]——次谐波，如果电机转子的换向器有8个换向器片，电刷经过每个换向器片产生1个纹波（基波），则[x18t]是电机的每秒旋转的周数；[x1t]——纹波的基波；[x2t]——纹波二次谐波；[xn（t）]——纹波[n]次谐波；[n（t）]——噪声。

电机纹波的谐波产生机理与半导体器件非线性产生谐波的机理不同。电机纹波的谐波是由于电机碳刷在旋转时跨接换向器片时，因电机绕组的阻抗并联效应、电机定子/转子磁场的交互、碳刷与换向器片之间的接触不理想等因素产生的。如相邻换向器片间填充物磨损造成的碳刷径向起伏、换向器片边缘的翘起/凹陷以及毛边在正反换向时引起的碳刷径向跳动、碳刷与换向器片磨损划痕造成的非均匀接触、碳刷与换向器片间接触面存在碳粉与金属颗粒引起的接触间隙、电枢的同心度不良或轴承偏心、碳刷与换向器片间电火花等。这些缺陷在电机旋转时都会造成碳刷与换向器片间部分接触面微观上的跳空或按压力不足，反映在纹波波形上就是各种纹波波形的畸变/缺损/M凹陷等。对某一电机，每换向器片所产生的纹波畸变方式与谐波成分不同，不同电机个体之间的纹波特性也不同，而且随着电机负载（反映到电流上）、电机转速的变化而变化。因而纹波各次谐波之间以及与基波之间的初始相位基本没有依赖关系。

虽然对“纹波”而言，[x1t]是纹波的基波，[x2t]是纹波的纹波二次谐波，[xn（t）]是纹波[n]次谐波，但从信号的一般性表达，基波与谐波是相对的，确定基波频率后谐波便是基波频率的[n]倍（[n≥2]）；例如也可以将[x14t] 看作信号的基波，则其二次谐波为[x12t]，三次谐波为[x34t]，四次谐波为[x1t]；也可以将[x12t] 看作信号的基波，则其二次谐波为[x1t]，三次谐波为[x32t]，四次谐波为[x2t]，[… ]；习惯上将[x1t] 作为通用信号的基波，其二次谐波为[x2t]，三次谐波为[x3t]，四次谐波为[x4t]，[… ]。无论通用信号的基波如果选择，上述关于基波与谐波之间相关变换的性质都是成立的。

2.2" 信号相关变换定义

设相关运算的输入序列是周期慢变的准周期性信号，当相关运算的本地序列取自输入信号序列当前周期起点的前M（M是≥1的整数）个周期，且经每个信号周期本地序列动态更新一次，用此本地序列与当前周期输入信号序列各采样点从始至终逐点滑动做相关运算，相关运算的输出序列称为该周期输入信号序列的相关变换输出，此相关运算的过程称为信号的相关变换。

由此可见，实现信号相关变换的系统是有记忆的系统，记忆深度是输入信号序列的M个周期。

信号相关变换的特殊之处是其本地序列的周期动态更新以及本地序列长度（也是相关运算的长度）的相应更新。对于一个信号采样率固定不变的系统，当信号周期变化时，其连续M个周期采样序列的样本数也会相应变化。对一特定周期的输入信号序列相关变换，本地序列及其长度是固定不变的。M值的确定由两个因素决定，一是系统中允许的信号处理时延，二是连续M个周期内信号周期变化不大。相关变换的本地序列每间隔一个信号周期更新一次，以保持本地序列与输入信号序列的相似性。由此可见，一个准周期信号序列的相关变换，是对当前输入的单周期信号序列，用固定的本地序列逐采样点滑动的相关计算。每完成一个输入信号周期序列数据的相关变换后，更新一次本地序列，更新方法类似移位寄存器，只是每次更新一个周期的采样点，即本地序列的头部增加刚完成相关变换的信号序列，尾部去除最后一个周期的信号序列，更新后的本地序列仍然是M个信号周期，但由于加入的新的单周期序列的采样点数与移出的最老的单周期序列的采样点数可能不同，更新后的本地序列的采样点数可能不同，用更新后本地序列的实际长度作为下一周期信号序列相关变换的相关运算长度。

2.3" 纹波信号的相关变换

为简明起见，将纹波信号数学表达式中低于基波频率的次谐波成分忽略，纹波信号数字表达式为：

[xpt=k1⋅x1t+k2⋅x2t+k3⋅x3t +…+kn⋅xnt+nt]

式中：[x1t=cos（ω1t+θ1）]是基波信号；[x2t=cos（ω2t+θ2）]，[x3t=cos（ω3t+θ3）]，[xnt=cos（ωnt+θn）]是谐波信号；且有[ω2=2ω1， ω3=3ω1， ωn=nω1]；初始相位[θ1，θ2，θ3，…，θn]是[[0，2π）]期间的随机值。

纹波信号的相关变换输出可表示为：

其中 [τ∈[0，T1）]，展开第1项如下，

利用三角函数的相关运算的特性：

在[ω2≠ω1]情况下，其相关变换输出[ct=12c1t+c2t =0]；在[ω2=ω1]情况下，其相关变换输出[12⋅T1⋅cosΔθ]，即[c][t=12⋅T1⋅cos][ω1τ]。

可知[0T1x1tx2t+τdt=0]，[0T1x1tx3t+τ]

[dt=0]，…，[0T1x1txnt+τdt]=0，得：

[0T1x1txpt+τdt=k10T1x1tx1t+τdt+0T1x1tnt+τdt=k1T12⋅cosω1τ+N1t]

同理可得，

[0T1x2txpt+τdt=k20T1x2tx2t+τdt+0T1x2tnt+τdt=k2T12⋅cosω2τ+N2t]

……，

[0T1xntxpt+τdt=kn0T1xntxnt+τdt+0T1xntnt+τdt=knT12⋅cosωnτ+Nnt]

由此得，纹波信号的相关变换输出为：[Rpt+τ]

[T12[k21cosω1τ+k22cosω2τ+k23cosω3τ+…+k2ncosωnτ+Ntotal]，]其中[τ∈[0，T1）]。

从纹波信号相关变换输出的表示式可以看出，纹波信号相关变换的输出仍然包括基波、二次谐波、三次谐波等各次谐波。且相关变换输出的基波频率与原始纹波信号的基波频率相同，即纹波相关变换输出的波形与原纹波信号波形具有相同的周期。另外一个非常重要的特性，相关变换输出的基波和各次谐波的系数[k2i]都是正值，相关变换输出的相位初值都是0。因此，纹波信号相关变换输出的波形，在其基波的上峰位置，各次谐波的贡献都是正的，是同相叠加的，使得在基波上峰位置一个邻域内的波形变得尖锐且不会出现任何凹陷。

由此可见，即使受到具有不同初始相位的各次谐波干扰而变形严重的纹波信号，经过相关变换后，基波和所有次谐波的初始相位全都归零，相关变换的输出在基波的上峰位置，各次谐波不但不会干扰基波的上峰，而且还会使上峰附近的波形变得更清晰，信噪比更高。可以利用这个特性，在相关变换输出的波形上测量纹波的周期，即测量两个上峰之间的时间间隔，代替在原始纹波波形上测量纹波周期。另外值得注意的是一个相关变换的优良特性，纹波经过相关变换后，原纹波中基波与谐波之间、不同频的谐波之间的乘积项在积分区间被相互抵消，随机噪声也因相关变换的积分滤波效应而降低，相关输出的各谐波相位被同步，各谐波成分不再有害反而变得更有利于提高周期测量精度。即使谐波相对功率很高、变形严重、传统周期估计十分困难的纹波，在相关变换的输出域，其波形上峰立即变得尖锐高耸清朗，纹波周期估计也变得十分轻松而且精度高，纹波计数不会漏计或多计。

2.4" 非整数周期相关变换的性能

当相关变换的本地序列长度[N]不是1个或整数倍个纹波周期对应的采样点数时，基波与谐波相互间相关变换的输出不再为0，下文对此种情况下的相关输出进行分析。

相关运算是一个积分运算，具有分段可加性，相关运算表示为 [Ck=j=0（N-1）Ak+j⋅Bj ] ，设纹波ADC的采样率为[K]采样点/秒，可将[N]分解为：N = M + m，其中[M]是[N]/[K]的最大整数，[m]是（N mod K）的余数，则相关运算可表示为：

[Ck= j=0（N-1）Ak+j⋅Bj =j=0（M-1）Ak+j⋅Bj +j=M（M+m-1）Ak+j⋅Bj ]

根据前述讨论可知，当[A]与[B]为基频或谐波的信号序列时，如果二者的频率不相同，则有 [j=0（M-1）Ak+j⋅Bj ]=0，此时[Ck=j=M（M+m-1）Ak+j⋅Bj ]。

所以只要相关变换长度取得略长一些（如4个纹波周期），频率不同的基波与各次谐波以及各谐波间的相关变换，在整数个纹波周期内互相关能量在积分（累加）过程中被相互抵消，剩下不足1个周期的互相关能量在积分（累加）过程中部分被抵消，被整个相关变换时段平均后，仍能呈现出整周期相关变换长度所具有的特性，只是有一定的剩余误差；相关变换后基波频率成分和各次谐波频率成分在基频上峰点位置能量同相叠加的特性仍然成立；总之相关变换后的上峰附近仍然具有较高的信噪比，纹波周期估计仍能正确进行，这种情况主要处于纹波周期估计的初始阶段。

3" 仿真验证

3.1" 三角信号整周期相关运算特性的仿真验证

两连续函数的乘积在一定时间范围内的积分，在离散时间情况下就是相关运算过程。以下通过仿真对“余弦信号与其谐波之间的相关运算特性”进行验证。

仿真时，采样率为100ks/s，基波信号频率为1kHz初始相位为[π/4]的正弦，二次谐波为2kHz初始相位为[π/6]的正弦，三次谐波为3kHz初始相位为[π/3]的正弦。产生的基波信号长度为5个周期。仿真时输入信号序列和本地序列可以分别是基波、二次谐波、三次谐波、（基波+二次谐波+三次谐波）。为了显示方便，本地序列显示波形下偏移-3.0，相关变换输出显示波形下偏移-6.0。以下观察相关变换仿真结果。

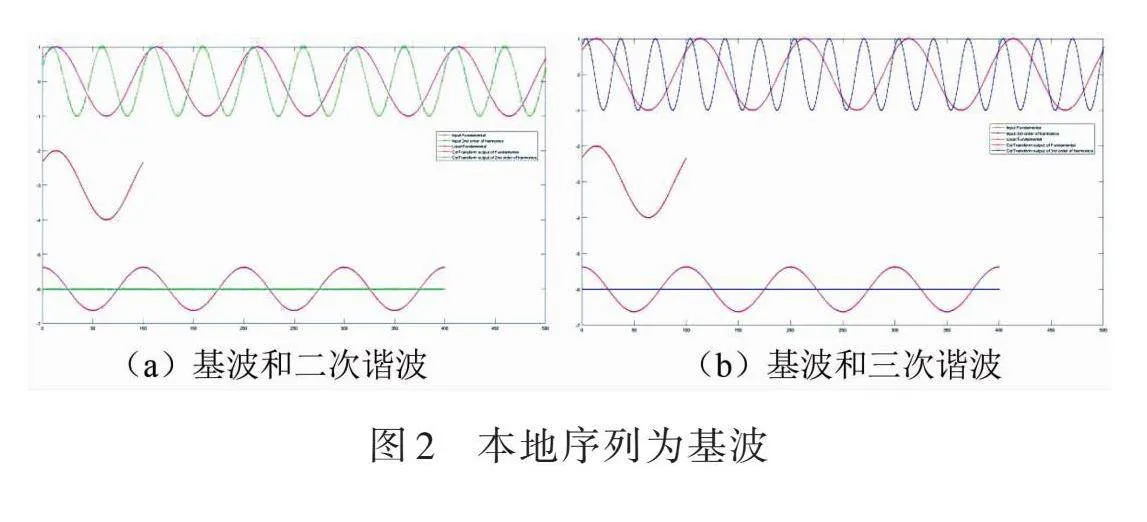
图2a和图2b中，本地波形皆为基波，且其初始相位与输入信号中的基波初始相位相同。在图的下部展示了输入分别为基波与谐波时相关运算的输出波形。图中相关运算输出曲线的每一个点，对应的是本地波形的起始点移动到该点位后，与输入信号波形对应位置段的数据进行相关运算（逐点点乘再累加）所得的值。从图2a中可以看到，本地基波与输入基波（同相位）的相关运算输出是一个初始相位为0的余弦波形，且其频率与本地或输入的基波频率相同；本地基波与输入二次谐波（同相位）的相关运算输出也是一个初始相位为0的余弦波形，且其频率与本地或输入的二次谐波频率相同。从图2b中可见，本地基波与输入基波（同相位）的相关运算输出同样是一个初始相位为0的余弦波形，频率与本地或输入的基波频率相同；本地基波与输入三次谐波（同相位）的相关运算输出恒为0，且与初始相位无关。

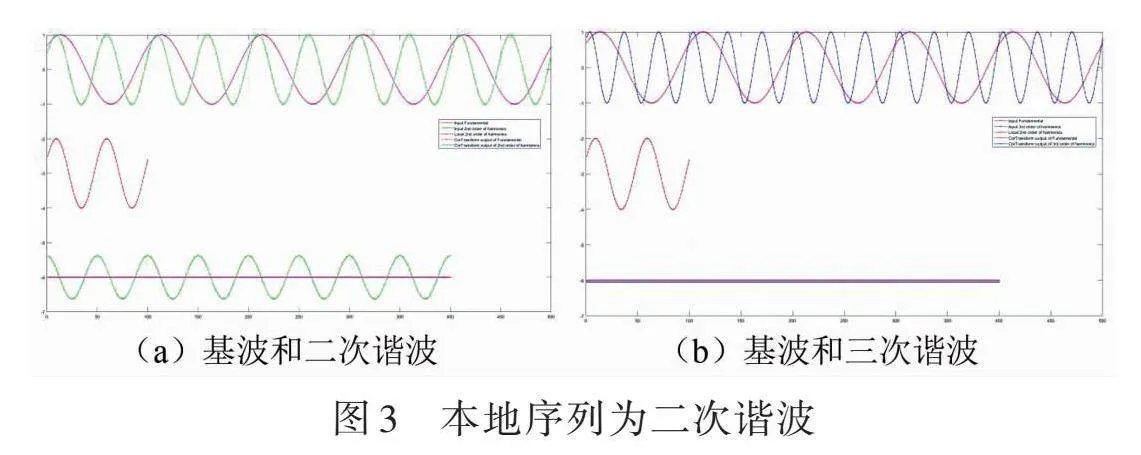
图3a和图3b中，本地波形均为二次谐波，其初始相位与输入信号中的基波初始相位相同。在图的下部显示了输入分别为基波与谐波时相关运算的输出波形。图中相关运算输出曲线的每一个点，对应的是本地波形的起始点移动到该点位后，与输入信号波形对应位置段的数据进行相关运算（逐点点乘再累加）所得的值。从图3a中可以看出，本地二次谐波与输入基波的相关运算输出恒为0，且与初始相位无关；本地二次谐波与输入二次谐波（同相位）的相关运算输出是一个初始相位为0的余弦波形，且其频率与本地或输入的二次谐波频率相同。从图3b中可见，本地二次谐波与输入基波（同相位）的相关运算输出恒为0，且与初始相位无关；本地二次谐波与输入三次谐波（同相位）的相关运算输出也恒为0，且与初始相位无关。注：为了便于观察，此相关变换输出结果人为下移了-0.05（蓝色线）。

图4a和图4b中，本地波形都是三次谐波，且其初始相位与输入信号中的基波初始相位相同。在图的下部展示了输入分别为基波与谐波时相关运算的输出波形。图中相关运算输出曲线的每一个点，对应的是本地波形的起始点移动到该点位后，与输入信号波形对应位置段的数据进行相关运算（逐点点乘再累加）所得的值。从图4a中可见，本地三次谐波与输入基波的相关运算输出恒为0，且与初始相位无关；本地三次谐波与输入二次谐波的相关运算输出恒为0，且与初始相位无关。从图4b中可见，本地三次谐波与输入基波的相关运算输出恒为0，且与初始相位无关；本地三次谐波与输入三次谐波（同相位）的相关运算输出是一个初始相位为0的余弦波形，且其频率与本地或输入的三次谐波频率相同。

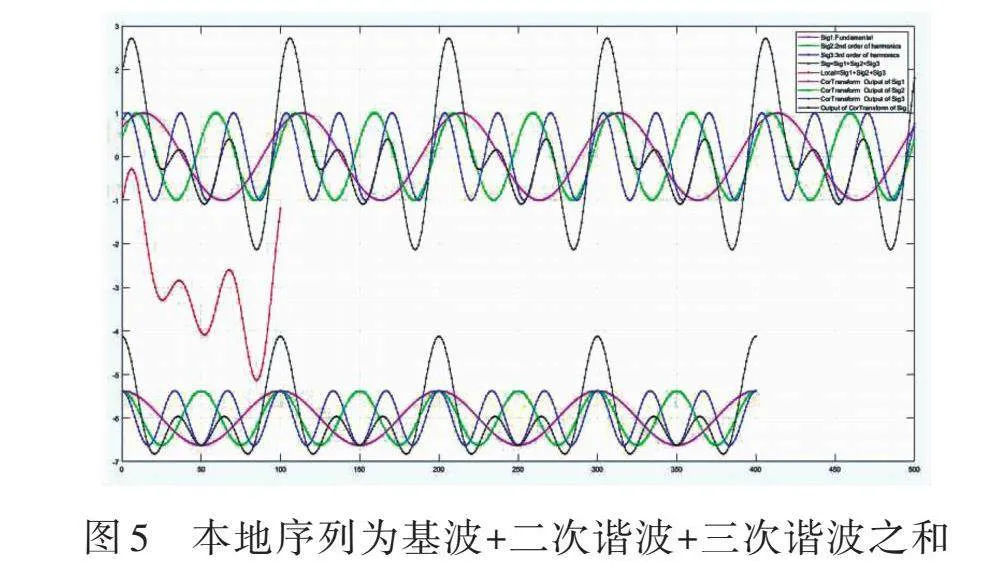
图5中的本地波形为（基波+二次谐波+三次谐波）之和，输入分别为基波、二次谐波、三次谐波、基波+二次谐波+三次谐波。因为此时本地序列里包含基波、二次谐波、三次谐波各分量，所以本地基波分量与输入基波相关运算输出基波同频的信号，本地二次谐波分量与输入二次谐波相关变换输出二次谐波同频的信号，本地三次谐波分量与输入三次谐波相关运算输出三次谐波同频的信号。本地（基波+二次谐波+三次谐波）与输入（基波+二次谐波+三次谐波）相关运算输出为独立基波输出+独立二次谐波输出+独立三次谐波输出之和。值得注意的是，相关运算输出的独立基波输出+独立二次谐波输出+独立三次谐波输出之和与输入（基波+二次谐波+三次谐波）及本地（基波+二次谐波+三次谐波）的波形是不一样的，因为独立基波输出+独立二次谐波输出+独立三次谐波输出中的每个频率成份都是零相位的，相加后的波形其上峰值处是同相完全叠加的。

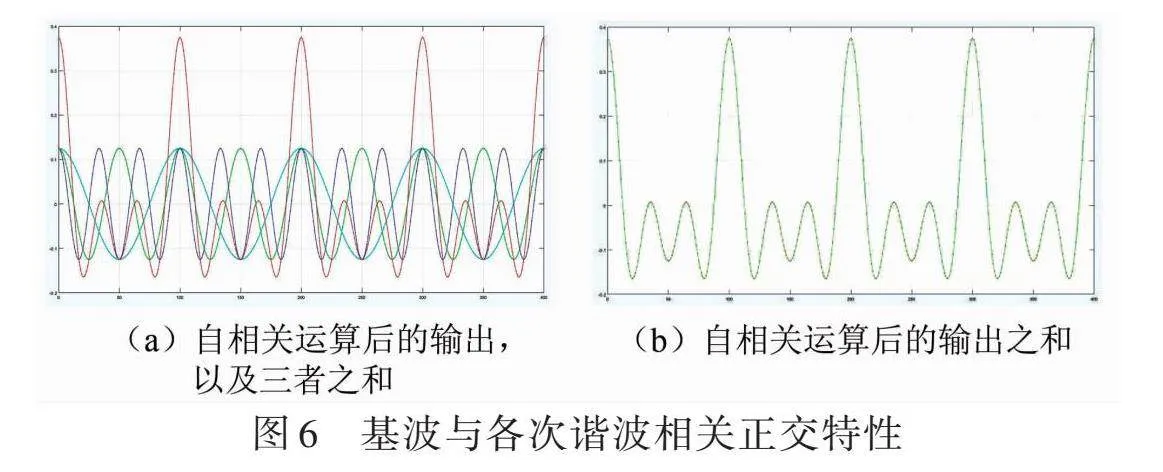
图6a是基波、二次谐波、三次谐波分别自相关运算后的输出以及三者之和（红色）；图6b是将图6a中的基波、二次谐波、三次谐波分别自相关运算后的输出之和（红色）与图5中基波+二次谐波+三次谐波自相关运算后的输出（黑色）进行比对，结果显示二者完全重合。这与理论分析结果完全一致。

3.2" 电机纹波信号相关变换及周期估计实例验证

车窗控制器通过对电机纹波进行累计计数来确定车窗玻璃的位置，同时依据电机纹波的周期确定电机转速，进而确定玻璃的升降速度。在电机纹波波形严重畸变的情况下，如何准确测量出纹波的周期，成为车窗电机纹波信号处理的关键所在。

上文所定义的信号相关变换，以及对其特性进行的理论分析与仿真结果均显示，利用相关变换来估计纹波信号周期，相较于传统直接对纹波波形进行整形与边沿检测，其可靠性与准确性要高得多。经过相关变换后的波形，基波与各次谐波的初始相位全部归零，在基波的上峰位置，基波与各次谐波同相叠加。因此，即使原始纹波中谐波相对功率较大且各次谐波相位分布杂乱，相关变换输出波形在基波上峰处的信噪比依然很高且不受影响。利用基波上峰间的时间间隔来估算基波纹波周期，能够得到十分稳定可靠的结果。相关变换的优良特性表明，相关变换几乎是电机纹波信号周期估计的最佳方法。

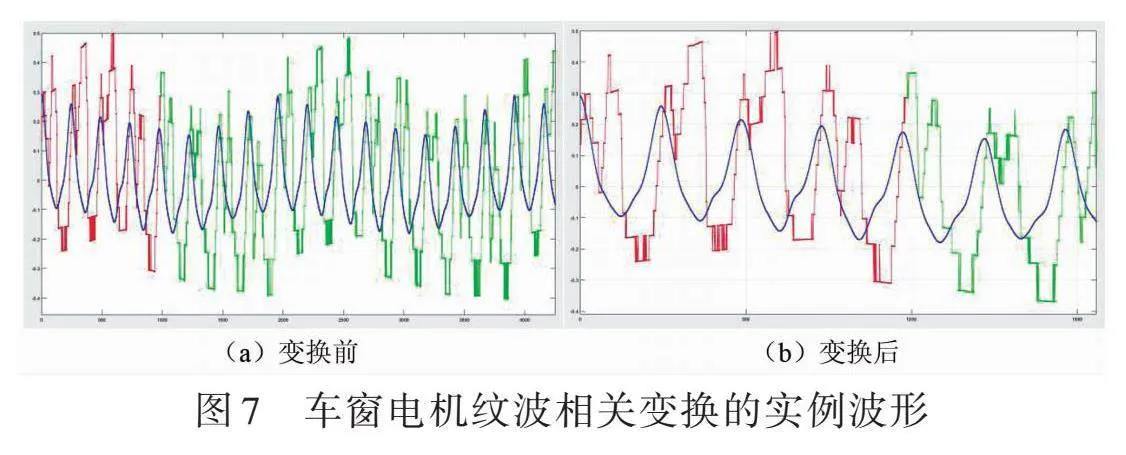
图7呈现的是车窗电机纹波相关变换的一个实例波形。在图中，红色与绿色波形为输入的待处理纹波波形，其中红色部分是从输入信号序列中截取的M=4个纹波周期波形，将其作为相关变换的本地序列，蓝色则是相关变换的输出波形。从图7a中可以看出，输入的纹波信号品质欠佳，部分纹波的凹陷深度超过50%，由于ADC分辨率的限制，波形的量化台阶十分明显，波形的上/下双峰不稳定，波形的直流成分也存在起伏。然而，经过相关变换后的输出，无论是波形还是周期都十分稳定可靠，上峰尖锐，峰间间隔非常稳定，如图7b所示。基于此相关变换输出，可以得到十分准确且稳定可靠的纹波周期。

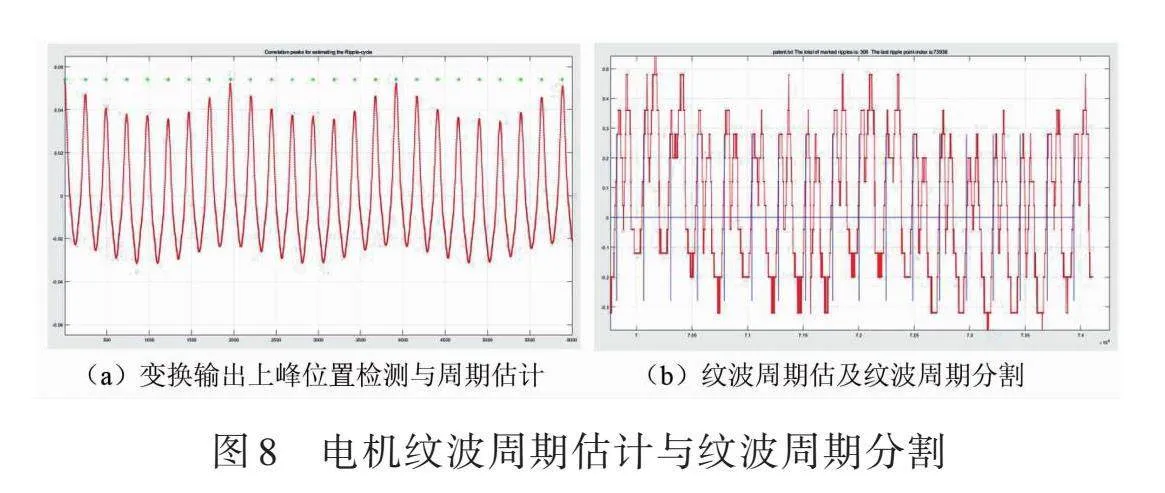
图8为一个电机纹波采用相关变换进行周期估计后对纹波时域波形进行周期分割的实例。图8a显示在相关变换的输出域进行上峰位置确定以及周期估计（相邻上峰的间隔）。图8b则显示利用在相关变换输出域得到的纹波周期对原始纹波波形进行周期分割。可以看出，即使在纹波波形较差的情况下，通过这种方式得到的纹波周期和波形分割点都十分准确且稳定。对故障电机采集的多种严重畸变的纹波波形进行处理的结果表明，本文中的相关变换纹波周期估计方法稳定可靠。即使在纹波严重畸变和噪声严重超标的情况下，相关变换输出的上峰形状仍然尖锐稳定可靠，能稳定地给出正确的纹波周期。

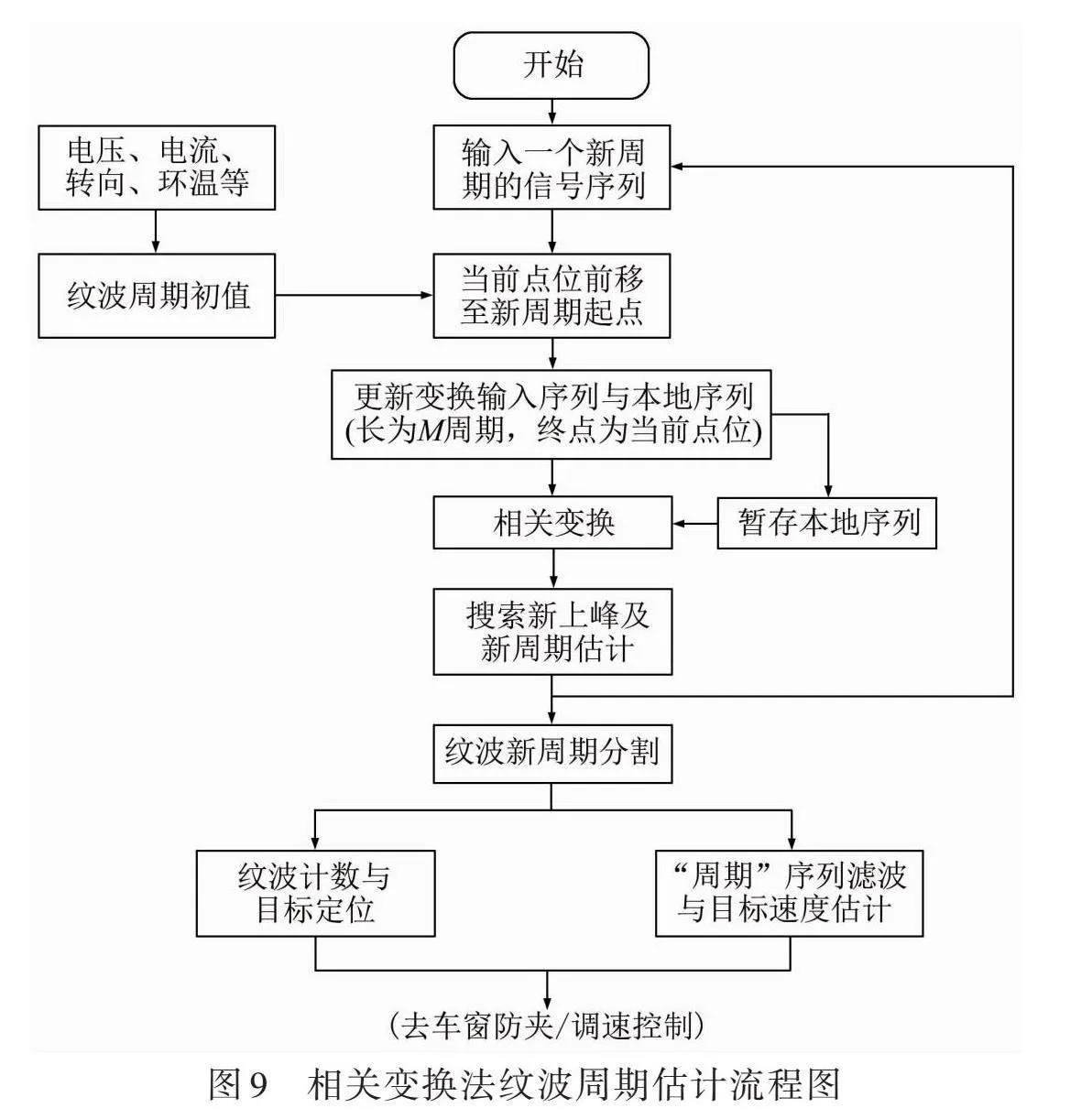
4" 相关变换纹波周期估计流程

相关变换法纹波周期估计流程如图9所示。首先，根据电机电流、电机电压、电机旋转方向以及环境温度等因素，可以粗略估算出初始纹波周期。随着ADC采样序列数据的不断到来，当缓冲区拥有M个周期长度的数据后，将这M个周期长度的数据暂存进本地序列的暂存区。此本地序列在对下一周期新进入的输入信号序列进行相关变换的过程中保持不变，至此，相关变换准备完毕。之后，新输入每一个信号采样点数据，就进行一次相关计算，直至完成共一个周期采样点数的新信号相关计算，得到一个周期采样点数的新信号相关变换输出，这标志着一个新周期输入信号相关变换的结束。接着，进行一次相关变换输出的上峰搜索与上峰位置时间计算，从而得到刚完成相关变换的信号周期值。此信号周期值可用于纹波周期波形分割、纹波计数以用于目标定位，经过滤波后还可用于目标速度估计。同时，此信号周期值也用于控制下一周期相关变换的本地序列与输入序列的更新，为下一周期的相关变换做好准备。依此不断循环，便能够不断求出每个到达纹波信号的周期估计值。

5" 小结

本文提出了一种新的纹波信号周期估计方法——相关变换法，并经过理论分析和仿真验证，证实了经过相关变换后的输出信号具有与输入信号相同的周期，且相关变换后输出信号的基波与各次谐波的初相为0，在信号基波的上峰处同相叠加，增强了上峰锐度和信噪比，提高了信号周期估计的准确性和可靠性。本文将相关变换方法应用于车窗有刷电机的纹波周期估计中，试验证明，即使纹波波形严重畸变，采用这种方法也能准确可靠地求得纹波周期。相关变换法仅需一至几个基波周期的信号长度，便能够在相关变换域准确估计出信号周期，既可以用于纹波信号分析，也可满足车窗定位、防夹与调速的实时在环控制要求。

参考文献

[1] GB 11552—2009，乘用车内部凸出物[S].

[2] 付朝辉.电动防夹车窗技术探讨[J].汽车电器，2012（7）：15-18.

[3] 李丹丹.车窗控制器及防夹算法的研究[D].哈尔滨：哈尔滨工业大学，2019.

[4] 周楠怡.基于电机纹波信号的车窗防夹系统设计[D].西安：西安电子科技大学，2021.

[5] 李云，徐洋，李超，等.基于电机电流检测的汽车电动车窗纹波防夹系统设计[J].汽车零部件，2021（1）：91-94.

[6] 王海青，李彦锋，杨天征，等.汽车玻璃升降系统防夹功能分析研究[J].汽车零部件，2020（1）：38-40.

（编辑" 凌" 波）