车辆稳定性因数自学习策略研究

【摘" 要】稳定性因数是表征汽车稳态响应的关键参数，对车辆横摆控制至关重要。由于影响稳定性因数的因素众多，如整车质量、质心位置、轮胎气压和侧偏刚度等，准确获取稳定性因数颇具难度。同时，车辆行驶过程中，轮胎磨损、胎压变化或轮胎型号改变等都会导致稳定性因数变化，进而影响车辆横摆控制。基于此背景，文章以稳定性因数理论模型为基础，结合车辆运动学方程，开发车辆稳定性因数自学习策略。实车测试表明，该方法能有效修正车辆稳定性因数，提升横摆控制效果。

【关键词】横摆控制；稳定性因数；自学习

中图分类号：U463.3"""" 文献标识码：A""" 文章编号：1003-8639（2025）01-0056-04

Research on Self-learning Strategy of Vehicle Stability Factor

LI Shunbo，WANG Zhenlong，LIANG Haibo

（Geely Auto Research Institute（Ningbo）Co.，Ltd.，Ningbo 315336，China）

【Abstract】Stability factor is a key parameter to characterize the steady-state response of vehicles，and it is very important for vehicle yaw control. Due to many factors affecting the stability factor，such as vehicle mass，center of mass position，tire pressure and side stiffness，it is difficult to obtain the stability factor accurately. At the same time，in the process of vehicle driving，tire wear，tire pressure changes or tire model changes will lead to changes in the stability factor，which will affect the vehicle yaw control. Based on this background，this paper develops the vehicle stability factor self-learning strategy based on the stability factor theory model and vehicle kinematics equation. The test results show that this method can effectively modify the vehicle stability factor and improve the yaw control effect.

【Key words】yaw control；stability factor；self-learning

0" 引言

稳定性因数K作为表征汽车稳态响应的重要参数，在车辆横摆控制中对目标横摆角速度的计算起着关键作用[1]。其数值决定了汽车的转向特性，当[K=0]时，汽车表现为中性转向；当[Kgt;0]时，汽车表现为不足转向特性；当[Klt;0]时，汽车表现为过多转向。通常车辆多表现为不足转向特性。

在车辆横摆控制中，一般使用整车实际横摆角速度[ωact]和质心侧偏角实际值[βact]来表征车辆当前的运动状态，同时通过目标横摆角速度[ωtarget]和目标侧偏角[βtarget]来体现驾驶员期望的运动状态。通过对状态偏差进行反馈控制，能够使车辆的行驶轨迹尽可能地接近驾驶员的预期[2]，从而提高车辆的操纵性和稳定性。因此，准确计算目标横摆角速度[ωtarget]显得尤为重要。而目标横摆角速度的计算又与车辆的稳定性因数息息相关。

稳定性因数[K]的值与车辆众多参数有关，包括‌整车质量、‌质心位置、‌轮胎气压和‌侧偏刚度等[3]。在车辆的行驶过程中，轮胎的磨损、胎压的变化、整车质量的变化或者轮胎型号的变化都会导致稳定性因数的变化。与此同时，在汽车动态运动过程中，稳定性因数与转向输入以及整车动力学状态（如横向加速度、横摆角速度及路面辅助特性等）息息相关。若不对其进行适应性修正，就会影响车辆的横摆控制效果，进而对车辆的操纵稳定性产生不良影响。

本文基于稳定性因数理论模型，依据二自由度整车模型和车辆运动学方程，开发稳定性因数自学习策略，并通过Simulink仿真及实车测试验证该策略的有效性。

1" 稳定性因数理论计算

在对稳定性因数进行理论计算研究时，需对车辆模型进行适当的假设：①忽略转向系统的影响，将前轮转角作为输入；②忽略悬架作用，认定汽车车厢仅进行平行于地面的平面运动，即只考虑y轴的侧向运动和绕z轴的横摆运动，此时，汽车沿z轴的位移，绕y轴的俯仰角与绕x轴的侧倾角均为0；③将汽车前进的速度[u]视为恒定值；④把侧向加速度限定在0.4g以下，以确保轮胎侧偏特性处于线性范围内；⑤由于驱动力不大，不考虑地面切向力对轮胎侧偏特性的影响；⑥忽略空气阻力的影响。

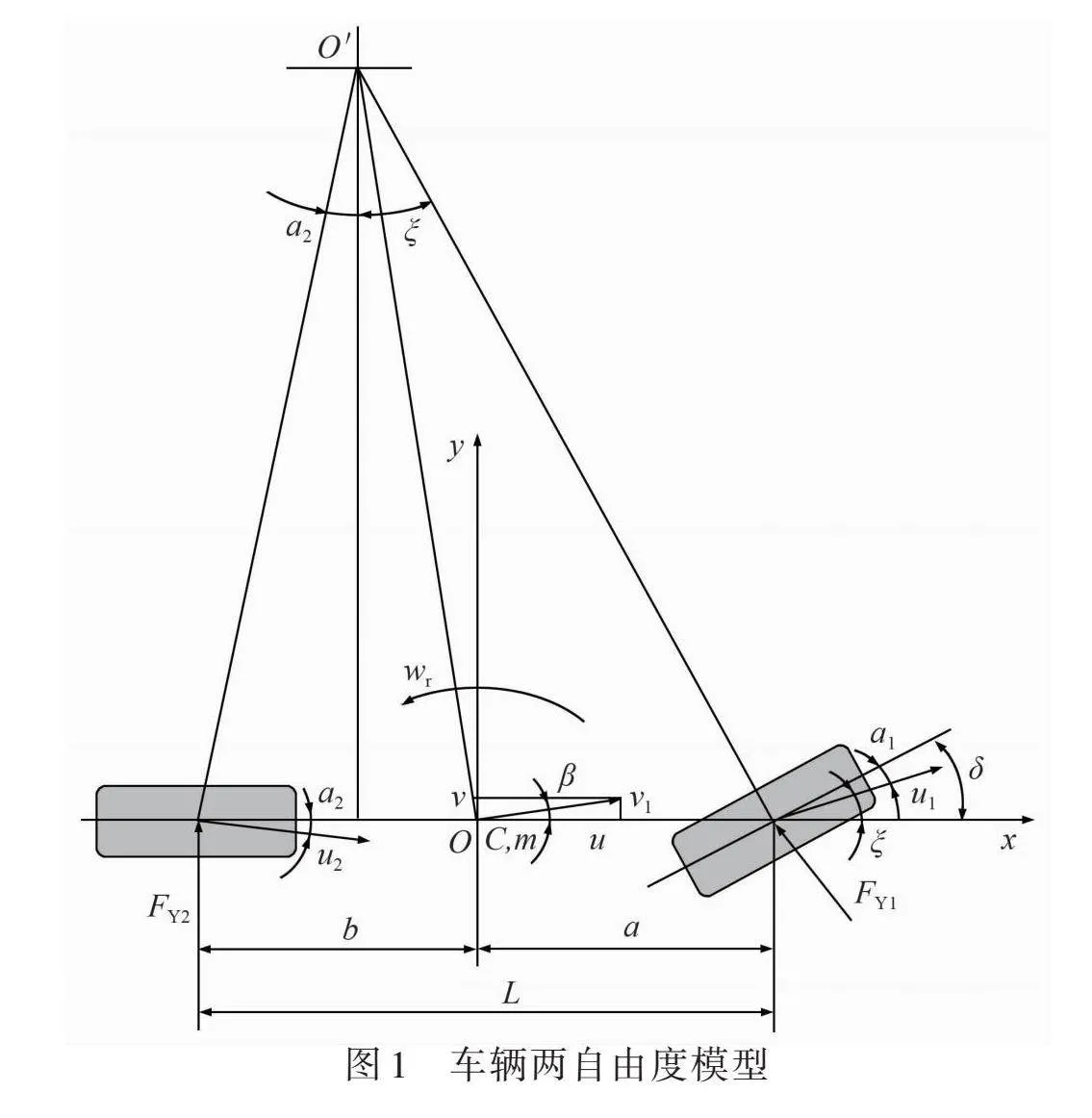
基于上述假设，汽车被简化为只有侧向和横摆两个自由度的模型。分析时，令车辆坐标系原点与汽车质心重合。车辆两自由度模型如图1所示。

根据牛顿第二定律，可以得到二自由度汽车运动微分方程式，即车辆曲线运动的方程[4]：

[mv+uω=kf+krβ+1uakf−bkrω−kfδIZω=akf−bkrβ+1ua2kf+b2krω−akfδ]

（1）

式中：[m]——整车质量，[kg]；[u]——车辆的纵向车速，[m/s]；[v]——车辆的侧向速度，[m/s]；[kf]——前轮侧偏刚度，[N/rad]；[kr]——后轮侧偏刚度，[N/rad]；[β]——质心侧偏角，[rad]；[a]——质心到前轴的距离，[m]；[b]——质心到后轴的距离，[m]；[δ]——前轮转角，[rad]；[IZ]——转动惯量，[kg·m²]；[ω]——横摆角速度，[rad/s]。

当车辆做稳态运动时，横摆角速度[ω]为定值，此时[v=0]，[ω=0]，代入式（1）得：

[muω=kf+krβ+1uakf−bkrω−kfδ0=akf−bkrβ+1ua2kf+b2krω−akfδ]

（2）

将式（2）两式联立，消去[β]，可以得到横摆角速度与方向盘转角的关系：

[ω=uLδ∙11+mL2（akr−bkf）u2] （3）

1.1" 理论模型计算

根据式（3），可得表征汽车转向特性的稳定性因数[K]表达式为：

[K=mL2（akr−bkf）] （4）

上式即为稳定性因数的理论计算公式。从式（4）可以看出，当车辆静止时，稳定性因数仅与车辆固有参数有关，这便是车辆的基础稳定性因数。然而，质心到前后轴的距离[a、b]及轮胎的侧偏刚度[kf]、[kr]受车辆的运动状态影响较大。例如，当车辆加速时，质心会向后转移，导致质心到后轴的距离减小，到前轴的距离增大；同时，载荷也会向后转移，使得后轴的侧偏刚度增大，前轴的侧偏刚度减小。这些情况都会影响稳定性因数。因此，有必要对车辆在运动状态下稳定性因数的计算方法进行研究。

1.2" 车辆运动学模型

根据车辆的稳态运动学方程（3）及式（4），可得：

[ω=VLδ∙11+KV2] （5）

由式（5）可以得到：

[K=（VδωL−1）/V2] （6）

式（6）即为车辆在稳态工况下的稳定性因数[K]的运动学计算公式。

在式（6）中，[ω、V]均可以通过传感器获得，[δ]为前轮转角，可通过方向盘转角获得，因而通过式（6）可以得到稳定性因数[K]实时计算的公式。

综上所述，稳定性因数由两部分组成，一部分是基础稳定性因数，即静态稳定性因数，这部分当车辆参数确定后固定不变；另一部分是动态稳定性因数，这部分随着车辆的运动状态而发生改变。因此，稳定性因数的计算需要综合考虑上述两种情况。

1.3" 稳定性因数自学习算法

当整车参数确定后，可由式（4）得到基础稳定性因数[Kb]，并将其作为当前稳定性因数[Kcur]的初始值[Kinit]。然而，由于车辆轮胎的磨损、胎压的变化、整车质量以及运动状态等因素的影响，实际车辆稳定性因数与基础稳定性因数存在一定偏差。当车辆稳态运动时，可由式（6）得到车辆的实时稳定性因数[Kact]。但由于车辆实际的运动很难保证稳态运动，故[Kact]的波动是比较大的，不能直接用于稳定性因数的修正。不过，车辆的稳定性因数[Kcur]应处于基础稳定性因数[Kb]和实时稳定性因数[Kact]之间。基于上述分析，采用局部寻优算法对稳定性因数[K]进行修正。

以目标横摆角速度与实际横摆角速度之差最小作为优化目标，得到：

[JP=ωtarget−ωact]" （7）

根据式（5），可得到[ωtarget]的计算公式：

[ωtarget=VLδ∙11+KestV2] （8）

[ωact]可通过传感器获得，联立式（7）、式（8）得：

[JP=VLδ∙11+KestV2−ωact]" （9）

式（9）即为稳定性因数[Kest]的优化目标。

设[Kinitlt;Kcur≤Kact]，采取如下步骤对稳定性因数[Kest]进行估计。

分别计算当[Kcur=Kinit]，[Kcur=Kact]，[Kcur=Kavg=Kinit+Kact2]时的优化目标函数[JP，init]，[JP，act]和[JP，avg]，将得到的3个数进行比较：①[JP，init]最小，说明稳定性因数[Kcur]不需要修正，[Kcur=Kinit]，寻优结束；②[JP，act]最小，说明稳定性因数[Kcur]等于实际稳定性因数，[Kcur=Kact]，寻优结束；③[ JP，avg]最小，说明稳定性因数[Kcur]介于[Kinit]和[Kact]之间，需进一步寻优。其中，针对情况③可以进行以下分析。

1）若[JP，initlt;JP，act]，则说明稳定因数介于[JP，init]和[JP，avg]之间，进一步计算当[Kcur=Kinit+Kavg2]的最优函数[J'P]。若[J'Plt;JP，avg]，则[Kcur=Kinit+Kavg2]，寻优结束；若[J'Pgt;JP，avg]，则[Kcur=Kavg]，寻优结束。

2）若[JP，initgt;JP，act]，则说明稳定因数介于[JP，act]和[JP，avg]之间，进一步计算当[Kcur=JP，act+Kavg2]的最优函数[J''P]。若[J''Plt;JP，avg]，则[Kcur=Kact+Kavg2]，寻优结束；若[J''Pgt;JP，avg]，则[Kcur=Kavg]，寻优结束。

以上，即为稳定性因数[Kcur]的寻优算法。

2" 稳定性因数自学习控制策略

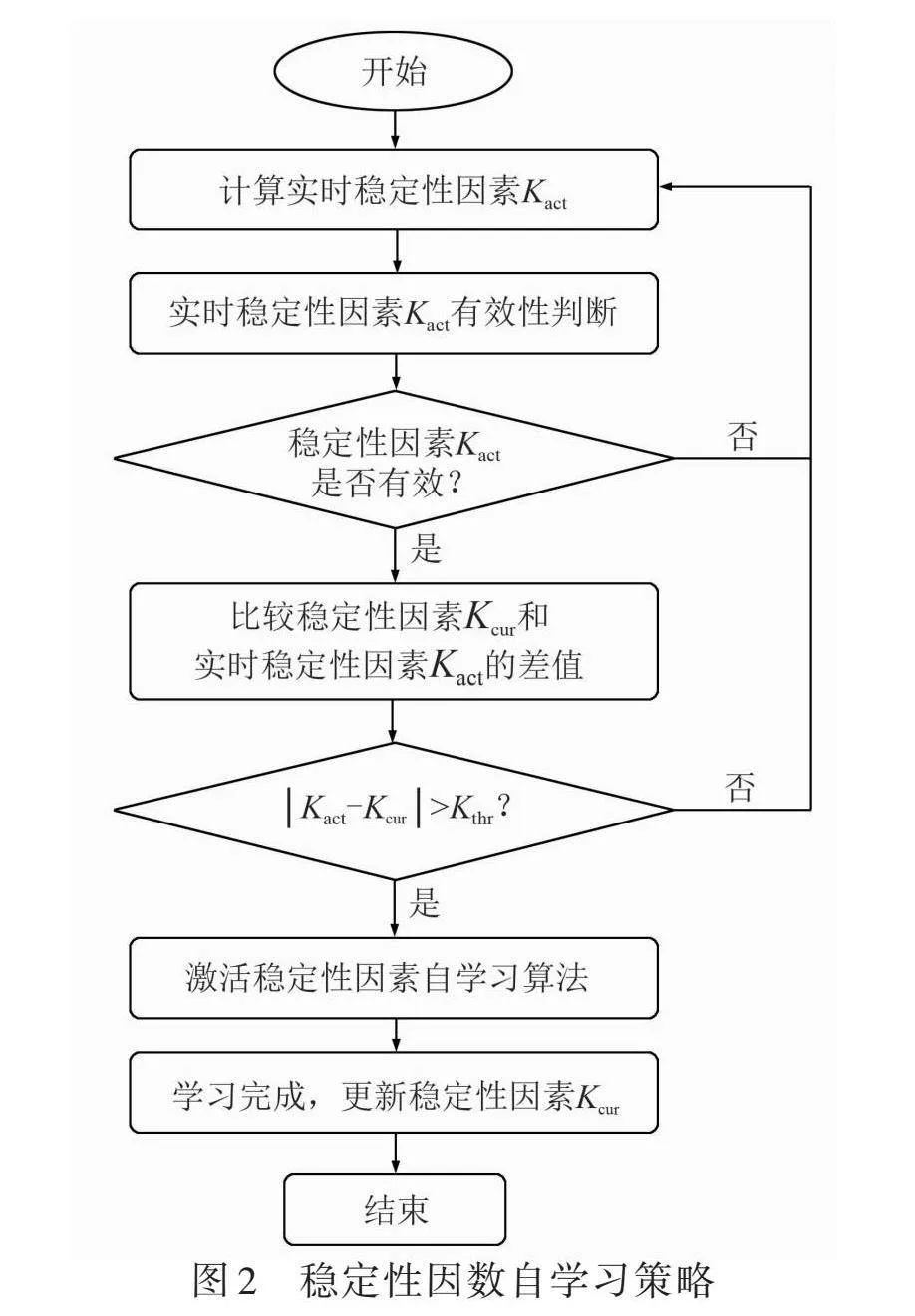
根据以上分析，设计稳定性因数自学习策略，如图2所示。从图2可以看出，稳定性因数自学习策略分为如下几个部分。

1）实时稳定性因数计算。根据式（6）计算实时稳定性因数[Kact]。

2）判断实时性稳定性因数的有效性。因为式（6）在车辆稳态运动下才能成立，即当满足如下条件时，实时稳定性因数[Kact]是有效的：①侧向加速度小于0.6g；②纵向加速度小于0.1g；③车速小于80km/h。

3）将当前稳定性因数[Kcur]与实时稳定性因数[Kact]进行比较，如果二者相差较大，则激活稳定性因数自学习算法；否则，保持当前的稳定性因数值[Kcur]。

4）稳定性因数自学习算法详见1.3部分描述。

5）稳定性因数自学习完成后，更新车辆稳定性因数。

3" 仿真模型搭建及实车验证

3.1" 仿真模型搭建

根据自学习控制策略搭建了仿真模型，该模型分为3个部分，如图3所示。

1）实时稳定性因数计算及有效性判断：计算实时稳定性因数[Kact]，并进行有效性判断。判断依据为当车辆处于稳态工况时，实时稳定性因数[Kact]有效。

2）稳定性因数自学习激活判断：当实时稳定性因数有效且当前稳定性因数[Kcur]与实时稳定性因数[Kact]相差较大时，激活稳定性因数自学习算法。

3）稳定性因数[Kcur]计算：根据1.3所述寻优算法，计算车辆稳定性因数。

3.2" 实车验证

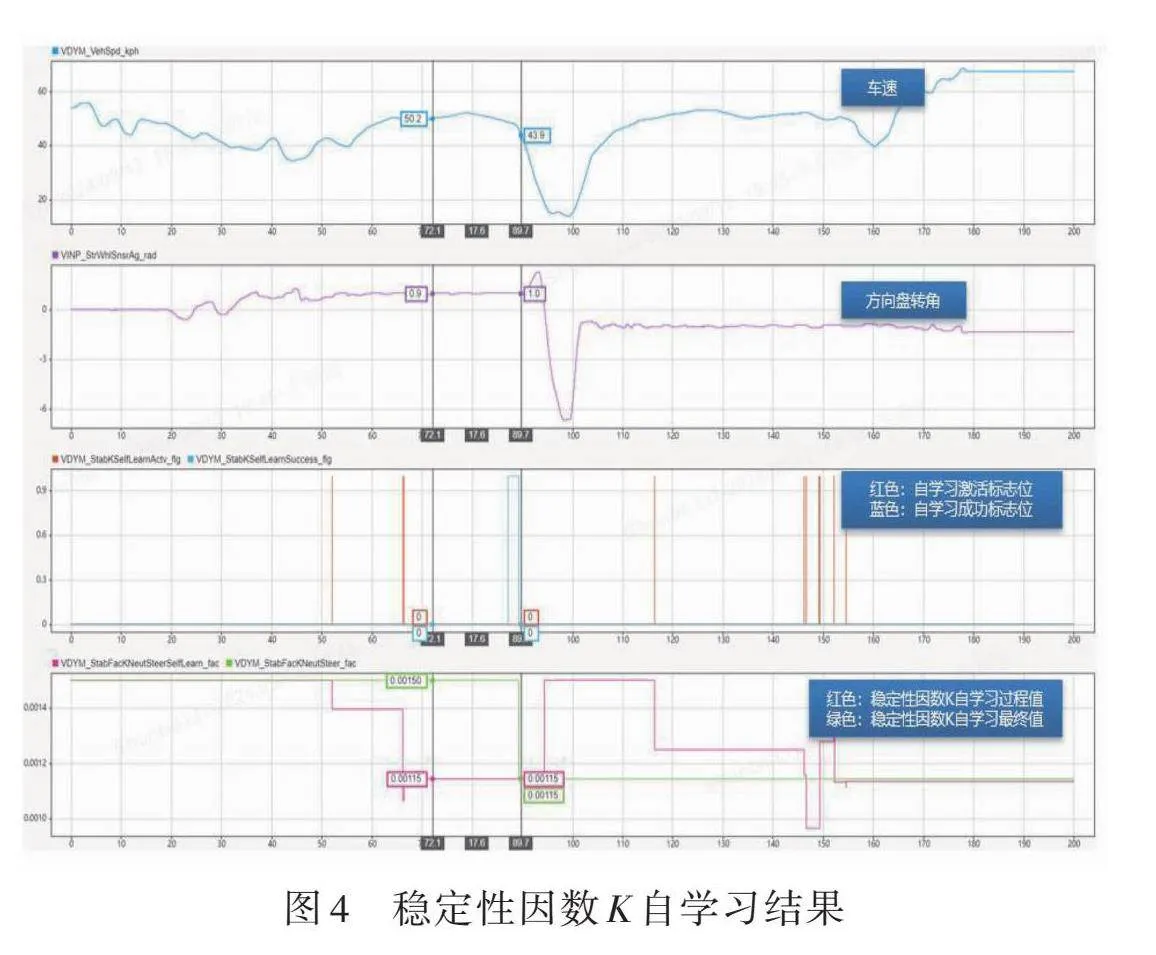
以某车型稳态绕圆工况（50～89ms）为例，稳定性因数自学习结果如图4所示。从图4可以看出，初始稳定性因数[Kcur=Kb=0.0015]。当车辆激活稳定性因数自学习策略后，稳定性因数[Kcur]调整为0.00115。

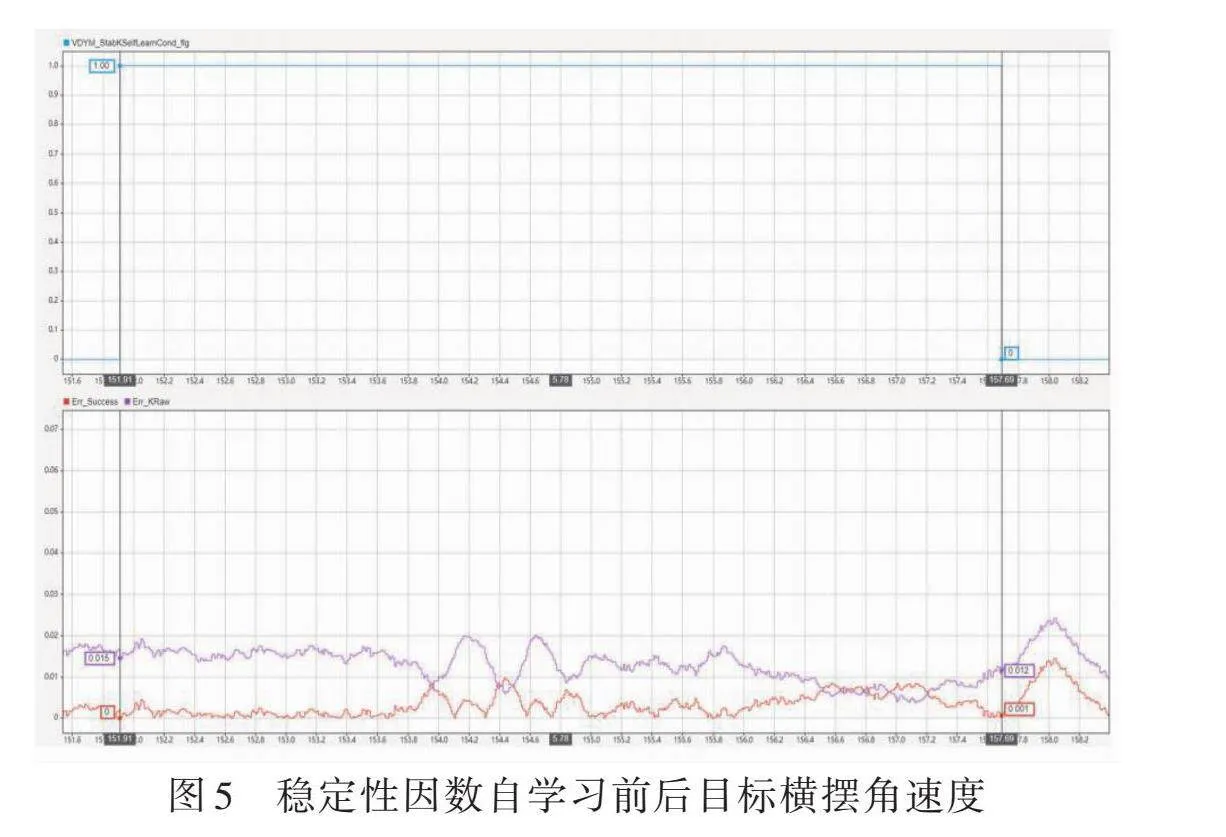
前文说过，稳定性因数对目标横摆角速度的计算准确性有关键性影响，图5展示了稳定性因数自学习前后目标横摆角速度计算的结果。

在图5中，紫色表示稳定性因数自学习前的目标横摆角速度与实际横摆角速度的差值，红色则为稳定因数自学习后的目标横摆角速度与实际横摆角速度的差值。从图中能够明显看出，在稳定性因数自学习后，目标横摆角速度与实际横摆角速度的差值最大值从约0.025rad/s变更为0.01rad/s，这表明目标横摆角速度的精度得到了大幅提高。由此可以得出，自学习策略有效且准确地对稳定性因数进行了修正。

4" 结论

总结前文内容，本文运用了稳定性理论因数理论计算模型以及运动学模型，采用寻优控制算法，设计出了稳定性因数自学习控制策略。通过实车测试表明，该算法能够有效提高目标横摆角速度的计算精度，进而提升车辆的稳定性和操纵性。

参考文献

[1] 余志生. 汽车理论[M].北京：机械工业出版社，2009．

[2] 李亮，宋健，于良耀，等．低附路面汽车动力学稳定性控制系统控制策略[J]．机械工程学报，2008，44（11）：229-235．

[3] 安部正人.车辆操纵动力学理论与应用[M]. 北京：机械工业出版社，2016．

[4] 何元超，李亮，宋健，等．极限工况下汽车动态稳定性因数模型与分析[J]．汽车安全与节能学报，2010（4）：320-328．

（编辑" 凌" 波）