基于DMC算法的冷轧板形多变量模型预测控制

摘 要：本文基于DMC算法，建立了冷轧板形的多变量模型，并进行预测控制。比较DMC模型与其他2种模型的控制效果可知，DMC模型在板形值波动、控制速度和优化效果方面表现更好。试验结果表明，DMC模型能够更稳定地控制板形，具有较快的调控速度，优化后的标准差较小，说明其在模型失配情况下的优化效果更佳。

关键词：DMC算法；冷轧板形；多变量模型

中图分类号：TG 334" " " " 文献标志码：A

冷轧板形控制是钢铁生产过程中的重要环节，对保证产品质量和生产效率具有重要意义[1]。传统的单变量控制方法已经不能满足板形控制要求，因此需要建立多变量模型以进行预测控制[2]。DMC算法是一种常用的预测控制方法，具有较好的性能和适用性。本文旨在基于DMC算法建立冷轧板形的多变量模型，并通过试验验证其控制效果。

1 基于DMC算法的冷轧板形多变量模型构建

1.1 预测模型

动态矩阵控制（Dynamic Matrix Control，DMC）是一种基于系统阶跃响应的预测控制算法，采用预测模型、在线滚动优化和误差反馈校正等机制，对系统输出进行有效控制。DMC算法主要由预测模型、滚动优化和反馈校正3个部分构成。其中，预测模型利用系统的单位阶跃响应模型来预测对象在未来时刻的输出值；滚动优化可以在每个采样时刻，根据预测模型预测的未来输出和设定的目标值，求解一个有限时域内的优化问题，进而将从优化问题得到的控制序列的第一个元素作用于系统，并在下一个采样时刻重复上述过程；反馈校正利用实际输出与预测输出间的误差来修正预测模型，以提高后续预测的准确性。

基于DMC算法的冷轧板形多变量模型构建是一个复杂的过程。首先，设置DMC控制器的采样周期为T。其次，每个采样时间点。即t=T，2T，…，NT下对应的单位阶跃响应采样值为a1，a2，…，aN-1。单位阶跃响应是指当系统输入发生单位阶跃变化时，系统输出的响应。对单位阶跃响应的采样值进行观测和记录，可以得到系统的动态响应特性。在DMC算法中，使用这些采样值来构建预测模型[3]。在NT时刻以后，单位阶跃响应应趋于稳定，此时aN的值约为阶跃响应的稳态值。原因是在足够长的时间内，系统的动态响应会逐渐消失，能够达到稳态。因此，aN的值可以用来估计系统的稳态响应。

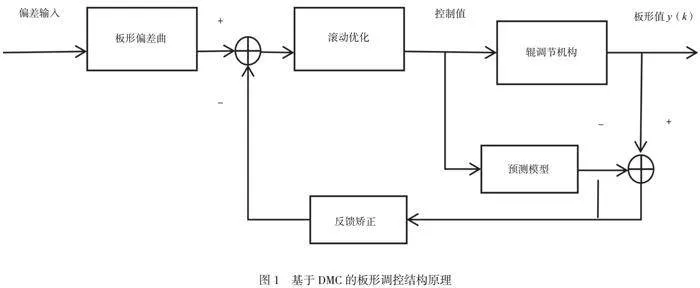
基于DMC的板形调控结构原理如图1所示。在DMC算法中，假设单位阶跃响应在NT时刻以后趋于稳定，即aN约为阶跃响应的稳态值。由于实际系统存在一定的动态响应，单位阶跃响应的采样值在初始时刻（t＜NT）还未达到稳态。因此，增加模型时域长度N0，更好地捕捉系统的稳态响应，使预测模型更接近实际情况。需要构建模型向量α，利用DMC算法中的预测模型对系统的响应进行预测和优化。模型向量α中的采样值提供了系统动态响应特性的信息，使DMC算法能够更准确地预测系统的响应，并根据预测结果进行相应调节[4]。

在DMC算法中，需要先构建模型向量α，它由各个采样时刻的单位阶跃响应采样值组成。再使用模型向量α来构建预测模型，预测系统在未来P个时刻的板形输出值，分别如公式（1）、公式（2）所示。

（1）

X（k）=X0" " " " " " " " " " " " （2）

式中：为列向量；，，…，（k+1|k）为未来P个时刻的输出预测值；N为单位阶跃响应的采样点总数，反映了系统动态特性的时间范围；X（k）为系统第k个采样时刻的单位阶跃响应值；X0为输出值，是控制开始时的系统输出。

根据线性系统的叠加原理，将未来P个时刻的板形输出值的预测表示为调控参数变化量的线性组合。在每个时刻，将调控参数变化量乘以对应的模型向量采样值，并将它们相加，即可得到对应时刻板形输出值的预测结果。

1.2 滚动优化

在DMC算法中，使用模型预测控制（MPC）来求解最优的控制量[5]。MPC可以建立系统的预测模型，并根据预测模型来优化控制量，以实现性能指标的最优化，如公式（3）所示。

（3）

式中：minJ（k）为控制输入的最小值；qi为误差权系数；Y（k+i）为时刻（k+i）的预测输出，其中k为当前时刻，是控制算法执行的时刻，i为未来时刻；（k+i|k）为控制输入的变化量，用于限制控制输入的剧烈变化；M、j为权重因子；rj为控制权系数；ΔX2为当前时刻相对于前一个时间步的控制输入的变化。

这些权系数在DMC算法中用于定义最优性能指标，为预测板形输出与目标板形间的差异，即误差项。将公式（3）改写成矩阵形式，如公式（4）所示。

minJ（k）=||YP（k）-||Q2+||ΔXM（k）||R2 （4）

式中：YP（k）为时刻k的预测输出向量；为时刻k的目标输出向量；Q为权系数矩阵，用于加权预测输出与目标输出间的误差；ΔXM（k）为k时刻的调控机构调节量；R为权系数矩阵，用于加权控制输入变化量。

利用优化算法计算出使性能指标最优化的控制量序列，并在每个时刻按照这个序列改变调控机构。在实际应用中，DMC并不会将调控机构变化量全部实施，相反，它采取了一种滚动优化的策略。具体来说，DMC只会在当前时刻k进行一步或数步优化，并在下一时刻，即（k+1）时刻重新进行优化。

1.3 反馈优化

在每个时刻，DMC算法会根据当前时刻的预测输出和优化计算结果来确定下一个时刻的输出。然而，在实际的生产中，由于内在因素或环境因素的干扰，预测值和实际值间不可避免会产生误差。这些误差来自于系统的不确定性、传感器的误差、外部干扰等因素。因此，为了提高控制的准确性和稳定性，需要引入ΔxM（k）预测值进行校正，以得到k时刻的调控机构调节量，如公式（5）所示。

ΔxM（k）=D[YP（k）-] " " " " " " " " " " （5）

式中：D为增益，用于校正预测值与实际值间的误差。

2 模型预测效果

为了验证基于DMC算法的多变量模型对冷轧板形调控效果的有效性，需要进行一系列试验和分析。在试验中，本文建立了基于DMC算法的多变量模型，该模型可以根据输入参数来预测冷轧板的形状。进而在实际的冷轧过程中获取输出的板形数据，用于验证模型的准确性和可靠性。在验证过程中，如果输出的板形数据与模型预测的结果存在偏差或误差，那么需要对控制器的参数进行调节。调节控制器的参数可以优化模型的预测能力，改进冷轧板形的调控效果。调节控制器参数的过程需要结合实际的板形数据和模型预测结果进行反复试验和调整，直到取得理想的调控效果。DMC参数见表1。

本文将ERMS作为偏差评价方法来衡量DMC模型对板形调控的准确性。比较不同算法的ERMS值可以评估不同算法在板形调控方面的性能差异。当DMC模型的ERMS值较小时，说明模型能够更准确地预测和控制板形，具有更好的调控效果。相反，如果其他算法的ERMS值较小，那么表明这些算法在板形调控方面具有较好性能。

（6）

式中：n为板形监测位置个数；yi为监测位置板形值；为监测位置板形值均值。

2.1 模型匹配情况下的控制效果分析

输入2条偏差曲线后，DMC模型能够迅速分析和预测系统的行为，并根据预测结果进行控制决策。对机构进行调节后，DMC模型能够在约100 ms内达到稳定状态，并使板形的偏差消除量达到最大值，表明DMC模型具有快速响应和调整能力，能够在短时间内优化板形。而最优控制算法和遗传算法在达到稳定状态和消除偏差方面需要更长时间。最优控制算法通常需要进行多次迭代和优化，以找到最优控制策略，因此调整时间较长。遗传（GA）算法需要经过遗传操作和优胜劣汰的过程逐步优化控制策略，同样需要较长时间。而DMC模型基于预测的控制方法，能够更快地调整控制参数，进而更快地达到稳定状态并消除偏差。与最优控制算法和遗传算法相比，基于DMC的预测模型在调控速度和精度方面表现更出色，能够进行快速响应和调整，最终优化板形，因此DMC模型在实际应用中具有重要意义，能够提高系统的调控效率和精度。

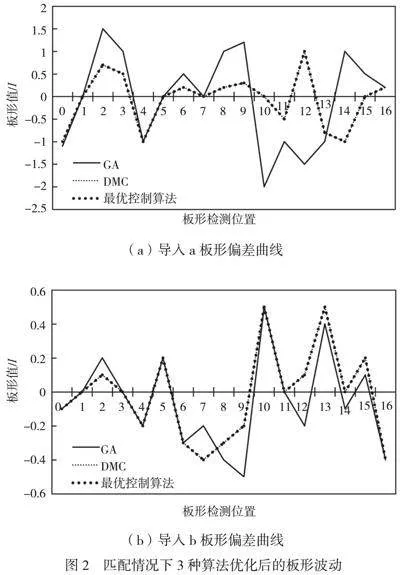
匹配情况下3种算法优化后的板形波动如图2所示。首先，DMC模型能够更稳定地控制板形，减少板形的波动性。对未来一段时间内的系统行为进行预测后，DMC模型能够提前调整板形，避免出现过度波动和不稳定现象。对系统进行预测并制定控制决策后，DMC模型能够及时对板形进行调整，使其保持在稳定状态，从而减少了板形的波动性。其次，基于DMC的预测模型在调控速度方面具有明显优势。对未来一段时间内的系统行为进行预测后，DMC模型能够预知系统的变化趋势，并根据预测结果制定控制决策。与其他2种模型相比，DMC模型具有更准确的预测能力和更高效的控制算法，因此响应速度更快，调整系统过程中的控制效果也更精确。

2.2 模型失配时情况下的控制效果分析

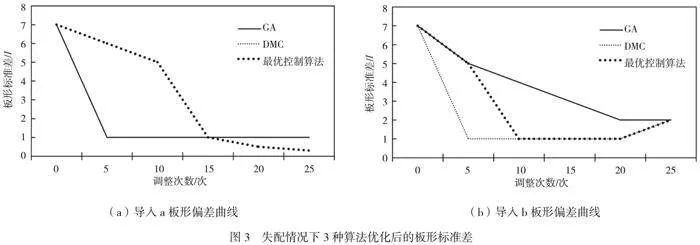
失配情况下3种算法优化后的板形标准差如图3所示。当模型失配时，分析控制效果可知，基于DMC的预测模型的调控速度比其他2种模型更快。基于DMC、最优控制算法和遗传算法优化后所得标准差分别为2.20 I、8.63 I、2.20 I和1.81 I、52.67 I、1.81 I，反映模型失配情况下板形的波动程度。标准差越小，板形的稳定性越高，模型的预测结果与实际情况更接近。本文中，DMC优化后得到的标准差较小，表明其预测结果与实际情况的匹配度更高，板形的波动程度更小，因此其稳定性更高。

在控制系统中，模型失配会导致预测结果与实际情况出现偏差，影响控制效果。因此，对模型进行优化至关重要。比较基于DMC、最优控制算法和遗传算法的优化结果可知，DMC优化后的模型在调控速度和稳定性方面具有显著优势，能够更快地响应系统变化，并在实际应用中保证控制系统的可靠性和准确性。

3 结语

本文基于DMC算法，建立了冷轧板形的多变量模型，并进行了预测控制。比较试验结果可知，DMC模型在板形值波动、控制速度和优化效果方面表现良好。DMC模型能够更稳定地控制板形，具有更快的调控速度，并且优化后得到标准差较小，表明其在模型失配情况下的优化效果更佳。本文结果对冷轧板形控制的实际应用具有重要意义。选择合适的模型和算法，能够提高板形控制的稳定性和效率，进而提升产品质量和生产效率。未来研究将进一步探索DMC算法在其他工业领域中的应用，并结合实际情况进行优化，以满足不同领域的控制需求。

参考文献

[1]丁海丽，陈宽文，刘朋远，等.基于双阶段网络模型的改进多变量广义预测控制[J].计算机测量与控制，2022（7）：141-147.

[2]任志玲，张倩.基于烟花算法的反应釜温度预测控制[J].控制工程，2024（3）：392-399.

[3]周克良，董世镇，张自建.基于改进磷虾群预测PID的电缆线径控制[J].传感器与微系统，2022，41（4）：96-99，103.

[4]徐梓榕，黄启泰，任建锋.基于超高斯函数的球形抛光工具去除函数库建立方法[J].激光与光电子学进展，2024，61（17）：1714009.

[5]张殿华，魏臻，王军生，等.冷轧板形数字孪生模型与协调优化信息物理系统[J].鞍钢技术，2023（5）：1-11.