浅水垫层消力池最佳深度研究

摘 要：浅水垫式消力池的深度是影响池内水跃流态的关键因素，为了确定浅水垫式消力池的最佳深度及与消力池入口弗劳德数的关系，本文设置试验装置并按比例建立模型，选取5种不同弗劳德数、6种深度的30个工况，根据大涡模拟方法设置合理边界条件后对各种工况进行研究。根据水跃流态、主流位置、消力池的水跃能量消能率等数据分析得出浅水垫式消力池的最佳深度比以及最佳深度和弗劳德数的关系。

关键词：消力池；最佳深度；弗劳德数；数值模拟

中图分类号：TV 65 " " " " " " " " " 文献标志码：A

许多水利工程下游采用水跃消能，其中，消力池在消能中起着重要作用[1]。但传统消力池存在近底部底流速度大、冲刷和空化破坏明显、消能率不够等缺点[2-3]。许多学者针对此类问题进行了研究，提出带浅水垫层的消力池概念，即在普通消力池上增加一个浅水垫层，在新型消力池结构中，可利用池底形成的水垫层对陡坡段水流施加柔性反作用力，“吸收”高速水流对消力池底板的冲击力，保护池底[4-5]。本文从水跃流态、主流位置和消能率3个方面对水垫的最佳深度采用有限元进行模拟分析，研究在不同弗劳德数下，具有浅水垫的消力池的所需深度。

1 研究方法

1.1 试验装置设置

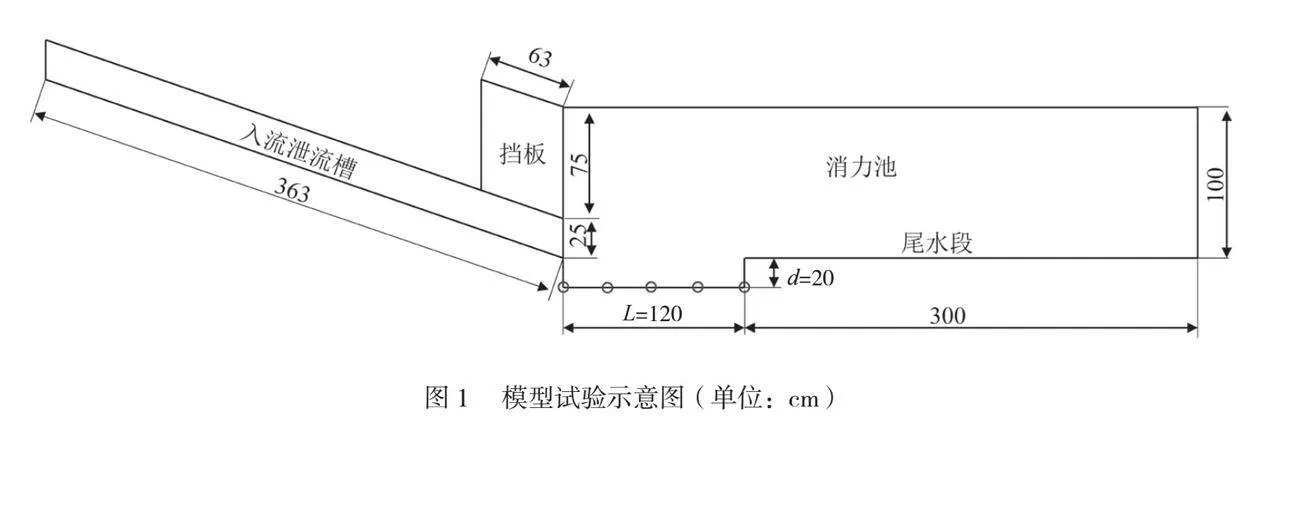
为了分析研究，本文设置了试验装置，剖面如图1所示，该装置包括长363cm的入流泄流槽、挡板、长120cm的带浅水垫的消力池和长300cm的尾水部分，出料槽段及所有下游部分横剖面为矩形，宽度为30cm，入口控制器是一个宽10cm的闸门，用于控制流入泄流槽的水位。本研究中使用的泄流槽的斜坡固定为17°，在下游控制水位，并采用出流条件。

1.2 模型设置

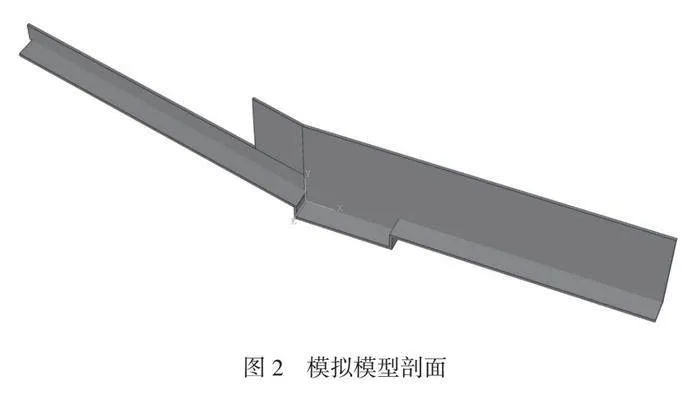
为了分析多种工况，对设置的试验装置进行一比一有限元建模，模型剖面如图2所示，将网格划分为5cm，模型总网格数约为246000个。将泄流槽入口的边界条件设置为速度进口条件，出口边界采用流出条件，采用壁函数法处理近壁的黏性亚层，将固定壁面设置为无滑移条件。

2 研究结果分析

研究采用大涡模拟方法进行模拟分析[6]，对表1中的5种典型弗劳德数、6种不同浅水垫层深度的30种工况进行系统研究，模拟了水跃流态、主流位置和单位体积消能率等水力特性，确定最佳浅水垫层深度。

2.1 水跃流态

由于不可能计算出每个深度，因此每个弗劳德数都选取相同的6个深度，分别为0cm、5cm、10cm、15cm、20cm、25 cm，每个对应弗劳德数下的最佳深度有±2.5cm的误差。

结果表明，相同弗劳德数和相同深度、不同弗劳德数的消力池，在不同深度的消力池内状态和流速分布不同。当弗劳德数相同时，若深度不够，则池内不发生水跃，且随着深度增加，水跃状态更加完整，例如当消力池深度为0cm和5cm时，消力池内不发生水跃，而当消力池深度为10cm、15cm、20cm和25cm时，消力池内发生水跃。当弗劳德数不同时，形成完整水跃所需的深度不同，例如当弗劳德数为7.64和6.92时，消力池15cm、20cm和25cm位置均发生完整水跃。当弗劳德数为8.05和9.25时，完全水跃发生在消力池深度为20cm和25cm位置。当弗劳德数为11.24时，完全水跃发生在消力池25cm位置。

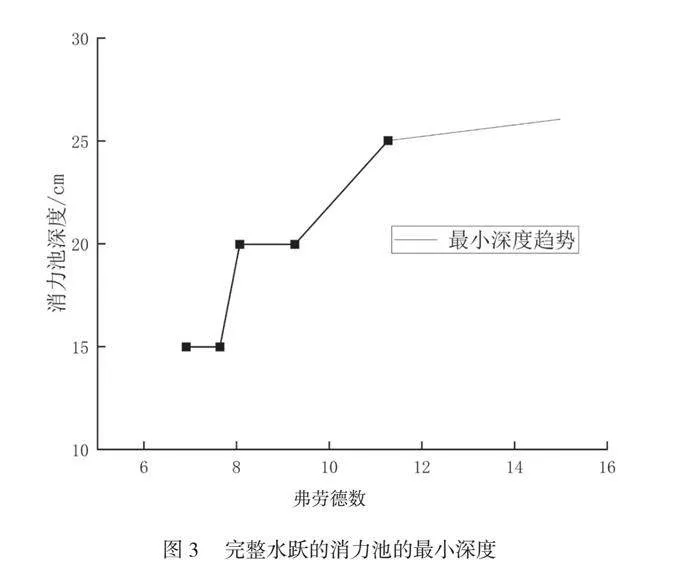
从水流流态的角度看，不同弗劳德数条件下的浅水垫式消力池的最小深度如图3所示。可以看出，弗劳德数越高，形成完整水跃所需的消力池深度越深。具体而言，在弗劳德数为6.92、7.64、8.05、9.25、11.24的情况下，浅水垫式消力池的最小深度分别为15cm、15cm、20cm、20cm、25cm。

2.2 主流位置

本文将流速大于断面平均流速的区域定义为主流区，将主流下边界以下的水体定义为水垫。从模拟结果可知，在某些情况下用速度等值面表示主流位置，结果表明，在发生水跃的情况下，最靠近池底的主流中心位于距池底约1/3深度，在弗劳德数为6.92、7.64和8.05时，可以清楚地观察到，在消力池深度为15cm、20cm和25cm的情况下，主流与垫底之间形成了水垫，而当弗劳德数为9.25和11.24时，在消力池深度为20cm或25cm的情况下，主流与垫底之间会形成水垫。

在30个工况中，对每个弗劳德数来说，水垫深度与消力池深度之比都随消力池深度而变化，见表2。由表2可以看出，在不同深度的消力池中，相同弗劳德数时，不同深度的消力池和相同深度时不同弗劳德数的消力池水垫厚度不同，对相同弗劳德数来说，消力池越深，水垫厚度越大，在相同水深下，弗劳德数越大，水垫厚度越小。

2.3 消能率

单位体积能量消能率的计算过程如公式（1）所示。

（1）

式中：ω为单位体积（无量纲）消能率；η=Ω/Ω0，无量纲体积；Ω为消力池容积，Ω=LdB；L、d、B分别为消力池长度、深度、宽度；Ω0为消力池入口与出口之间的水体积。

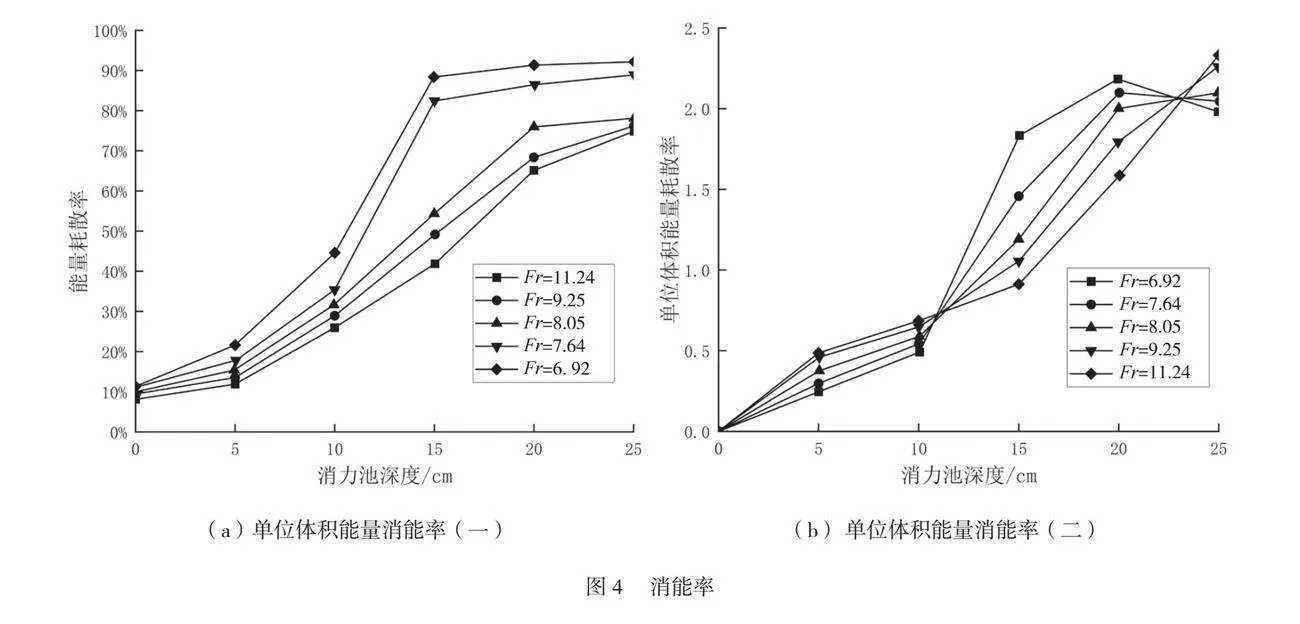
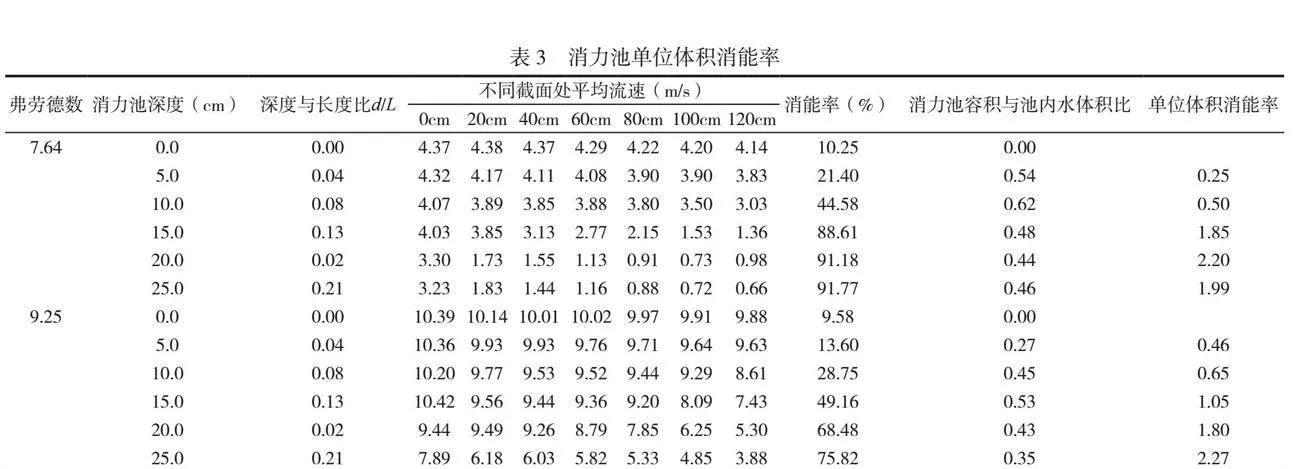
计算30个工况的消能率，结果见表3，本文仅列举弗劳德数7.64和9.25两种情况，其中，第三列为消力池深度与长度的比值（总长度为120cm）；4～10列为不同断面的平均流速（0cm、20cm、40cm、60cm、80cm、100cm、120cm分别表示断面距消力池入口处进水口的距离）。

利用表3的数据计算消力池的消能率和与消力池深度相关的单位体积消能率，并将不同的弗劳德数作为参数，如图4所示。

总的来说，总消能随池深增加而迅速增加，在达到一定值后变化不大，如图4（a）所示。而当弗劳德数较小时，单位体积消能率随深度增加先升高，达到最大值后降低，说明一些水体不涉及能量耗散，如图4（b）所示。当弗劳德数较大时，随深度增加而升高，这也说明总能量耗散达到最大值，但单位体积消能率未必达到最大值，说明消力池深度不足以形成水跃。例如当弗劳德数为9.25和11.24时，单位体积消能率随弗劳德数增加而不断升高，说明在25cm的深度足以达到本研究中的最大单位体积消能率。

3 消力池的最佳水深分析

对给定的弗劳德数来说，预计消力池中会发生完全水跃，底部附近的速度相对较慢，且总能量和单位体积的能量消散率较高。从水流流态、消能率和底部流速角度来看，消力池越深，越容易形成完全水跃，总消能率越高，主流距离池底越远，但从单位体积消能率的角度来看，水池中的部分水体不参与能量耗散，因此池深不宜过大，否则会造成浪费。另外，水垫厚度可能过大，因此不能将消力池视为浅水垫式消力池，其可能变成水垫式静力池，其消能性能与浅水垫式消力池有很大不同。因此，根据上述消力池的流态、主流位置、消能率等研究结果，可以得出以下浅水垫式消力池最佳深度标准。1）池内必须发生完整水跃。2）水垫厚度约为池深的1/10～1/3。3）消能率大于70%，且单位体积消能率尽可能大。

对不同的弗劳德数来说，仅用同一个标准无法确定最小值和最大值，因此需要满足3个标准才能得到范围。例如，对弗劳德数为6.92和9.25的情况来说，由流态和消能标准确定最小值，由消能率和主流位置确定最大值。取范围的平均值，将其作为浅水垫层消力池的最佳深度，随着弗劳德数增加，消力池的最佳深度也随之增加。

4 结论

本文选取5种不同弗劳德数、6种不同水深的30个工况，采用大涡模拟方法对消力池内的水力特性进行了数值模拟，包括水跃流态、主流位置和单位体积消能率等，得出以下结论。1）本文根据水跃流态、主流位置及消能率的试验结果，总结了浅水垫消力池最佳深度的3个标准：池内必须出现完整水跃；水垫厚度约为池深的1/10～1/3；消能率大于70%，且单位体积的能量耗散率尽可能大。2）结果表明，浅水垫式消力池的最佳深度比（深长比）为0.14～0.26，且浅水垫式消力池的最佳深度随弗劳德数增加而增加。

参考文献

[1] 谢高鹏，张琛.某水库泄洪闸消力池长对池内水力特性影响的分析[J].河南水利与南水北调，2023， 52（11）： 65-66.

[2] 龙跃洲，潘世一，黄忠，等.溢洪道泄槽及消力池流态优化数值模拟研究[J].水电与新能源，2023， 37（6）： 26-29.

[3] 宋涛.水库溢洪道消力池结构宏观体型优化研究[J].甘肃水利水电技术，2023， 59（1）： 60-64.

[4] 刘达，廖华胜，李连侠，等.浅水垫消力池的大涡模拟研究[J].四川大学学报（工程科学版），2014， 46（5）： 28-34.

[5] 刘达，李连侠，廖华胜，等.不同入流角度对浅水垫消力池水力特性的影响研究[J].水力发电，2016， 42（4）： 49-52.

[6] 卢洋亮，尹进步，张曙光，等.跌坎突扩型消力池脉动压力大涡模拟研究[J].人民黄河，2022， 44（2）： 133-137.