轿厢系统水平振动最优快速终端滑模控制探究

摘 要：本文旨在探究轿厢系统水平振动的最优快速终端滑模控制方法，以提升其被控性能。研究人员通过建立轿厢系统水平振动的主动控制模型，确定系统的性能指标，为后续控制器设计奠定基础。在此基础上，研究人员设计了非奇异终端滑模控制器，并引入随机惯性权重粒子群算法对控制器进行优化，以实现系统振动的快速、精确抑制。研究结果表明，优化后的控制器能够有效减少轿厢系统水平振动，显著提升了控制系统的稳定性与响应速度。本文成果为电梯等轿厢系统的控制策略提供了新的方法，推动了相关领域的技术进步。

关键词：高速电梯轿厢系统；主动控制；终端滑模控制

中图分类号：TU 857 " 文献标志码：A

轿厢系统作为电梯的核心部件之一，其运行质量直接影响乘客的舒适度与人身安全。在运行过程中，轿厢的水平振动是影响乘坐体验的重要因素之一。传统的控制方法难以有效抑制系统的振动，尤其是在面对外部扰动变化较大或载荷快速变化的情况下，控制效果较差。为了解决这一问题，相关从业者积极尝试引入先进的控制策略来提升轿厢系统的运行性能。其中，快速终端滑模控制因其快速响应以及良好的鲁棒性而受到广泛关注。FTSMC通过引入滑模面与终端项来实现对系统的精确控制，在非线性、不确定性强的系统中具备优良的控制性能。本文通过优化控制器设计以及算法应用，期望能够有效提升轿厢系统的运行稳定性以及乘坐舒适度，为电梯技术的进步与安全运行提供新的技术支持。

1 轿厢系统水平振动主动控制模型

1.1 轿厢系统被控性能指标

1.1.1 乘坐舒适性

衡量轿厢乘坐舒适性的主要指标包括乘客在电梯运行过程中所感受到的加速度、速度变化以及振动等关键要素。一套设计精良的轿厢系统应当确保乘客在电梯起动、制动及速度变化的过程中，体验到的是平稳而连续的运动，避免出现突如其来的加速或减速以及不必要的震动[1]。这样的设计不仅极大地提升了乘坐的舒适度，更有助于降低乘客的不适感。

1.1.2 振动位移限制

轿厢的水平振动主要来源于电梯运行中的不平衡负荷、加减速过程中的动态影响以及外部环境的干扰。根据国际标准IEC 61508及相关行业规范，电梯轿厢运行时的水平振动位移应该被限制在最大允许位移范围内。例如，IEC 61508标准要求轿厢水平振动的最大位移应控制在±2mm以内。这一标准的设定旨在确保电梯在各种运行条件下都能保持平稳。电梯轿厢水平振动的来源主要包括以下5个方面。1）负荷不平衡。乘客或货物的分布不均可能导致轿厢在水平面上产生不规则的振动。2）加减速过程。电梯加速或减速时，动力系统的不稳定性会引起水平振动。3）轨道和导向系统的误差。轨道或导向系统的任何微小不平整都会引起轿厢的水平偏移。4）外部环境。建筑物的振动、风力以及其他外部因素也可能影响轿厢的水平稳定性。5）主动控制模型设计。为应对上述振动源，研究人员设计了一个有效的主动控制模型。主动控制系统通过实时监测和调整来抑制水平振动，其核心原理是使用控制算法与反馈机制来动态调整轿厢的稳定性。

具体实践中，系统需要配备高精度的传感器来实时监测轿厢的水平振动。以加速度计为例，研究人员将其测量范围设置为±10g，精度为0.01g，以确保对微小振动的敏感检测。此外，控制算法作为主动控制系统的核心，其算法包括PID控制、LQR控制以及自适应控制。PID控制算法通过调整比例、积分、微分参数来维持系统稳定。本文中，工作人员将PID控制器的比例增益设定为0.8，积分增益为0.1，微分增益为0.05，通过这种方式在不同的运行条件下有效抑制振动，反馈机制用于调整控制策略。系统会实时接收振动数据，计算当前振动与设定目标之间的差距，并调整控制信号。例如，如果实时振动位移超出设定的±2mm范围，系统将自动增加电动推杆的推力或调整液压阻尼器的阻尼系数，直至振动恢复到允许范围内[2]。

1.1.3 控制器饱和效应

控制器饱和效应是指当控制器输出信号达到其最大或最小限制时，无法进一步增强输出或调节能力的一种现象。电梯运行过程中，饱和现象会导致系统响应能力削弱，影响运行的稳定性。造成这种现象的原因如下：一方面，电机、阀门等控制系统的执行机构都有其物理限制。电梯用电机存在最大输出扭矩，如果控制信号要求的扭矩超过该值，电机将无法响应，导致控制器输出饱和。另一方面，控制器的设计参数设置不当，导致输出信号迅速达到饱和。具体实践中，如果一个PID控制器的比例增益设定点变化过快，输出信号就可能在短时间内达到最大限制。此外，在动态负载或环境条件变化的情况下，系统可能遭受不确定性干扰。例如，电梯满载加速时，控制器可能需要输出更大的力量以维持加速，进而导致控制器饱和。

当控制器输出饱和时，系统无法进一步调节状态。电梯在上升过程中，如果控制信号达到最大限制而无法提高，将导致电梯的加速度减小，可能使乘客感到不适。此外，饱和现象可能引发系统不稳定。如果控制器输出饱和，那么系统可能会出现振荡现象，特别是在负反馈控制系统中。研究表明，饱和引发的振荡周期可能高达5s，严重影响系统性能。饱和效应往往导致系统过冲，即实际输出超过设定值，随后又回落到稳定状态。这种现象在电梯的启停过程中尤为明显，导致电梯轿厢无法平稳停车，出现安全隐患风险。

1.2 构建轿厢系统水平振动主动控制模型

本次研究中，工作人员创建了一个典型的电梯车厢，该车厢质量约为1500kg，尺寸为2m×2m×3m。车厢通常由钢材料制成，其结构与质量会直接影响系统的振动特性。此外，钢丝绳作为电梯的主要承载组件，钢丝绳的弹性模量以及张力会在电梯运行中产生振动。工作人员选取ø10mm的钢丝绳，每根绳索的张力约为1000N。本次研究中，工作人员引入动力学方程，如公式（1）所示。

（t）=F总（t）-F 摩（t）-F弹（t）-F阻（t） （1）

式中：m为轿厢系统的质量；（t）为轿厢系统的加速度，即时间t上的二阶导数；F总（t）为作用在轿厢系统上的总外力；F 摩（t）为轿厢与导轨间的摩擦力；F弹（t）为由钢丝绳弹性以及导轨弯曲引起的弹性反作用力；F阻（t）为运动过程中的空气阻力或液体阻力。

具体实践中，工作人员利用公式（1）描述轿厢系统在运行过程中，质量与惯性力、摩擦力、弹性力以及阻力之间的动态平衡。它通过求解可以得到轿厢的加速度（t），从而可以计算任意时刻的位置与速度，进而进一步评估系统的运行状态，见表1。

2 最优快速终端滑模控制器设计

终端滑模控制（Terminal Sliding Mode Control，TSMC）作为滑模控制理论框架下的高级控制策略，其核心目标在于解决传统滑模控制在误差消除层面的不足。滑模控制凭借其迅速的响应能力以及对参数变化及外部干扰的不敏感性，成为线性及非线性系统控制的理想方式之一。需要注意的是，在具体实践中，滑模控制一般采用线性滑模面约束系统状态，这种方法虽然能够控制跟踪误差维持在特定范围内，但难以彻底消除误差。尽管通过调整线性滑模面参数能在一定程度上改变系统的收敛速度，并控制误差范围，但依旧存在显著的局限性。在此背景下，研究人员引入终端滑模控制技术，通过创新性地引入非线性终端项，精心设计了全新的滑模面，实现了系统跟踪误差在有限时间内精确收敛至零，突破了传统滑模控制的瓶颈[3]。非奇异终端滑模控制器的设计精妙地融合了滑模超曲面的定义与相应的滑模趋近律，确保了系统在整个控制周期内的稳定性以及卓越的动态性能。这一设计赋予了系统从任意初始状态迅速抵达滑模超曲面，进而达成预期控制效果的能力。

2.1 非奇异终端滑模控制器设计

本次研究中，工作人员先进行滑模超曲面的设计工作，设滑模超曲面为S，该曲面在控制过程中起到关键作用，通过滑模超曲面定义系统状态x的期望轨迹。本文中，电梯轿厢系统滑模超曲面如公式（2）所示。

s（x）=x-xd （2）

式中：xd为期望的目标位置。

系统在运行过程中，通过控制状态变量x与目标位置xd的差值来实现误差的稳定收敛，见表2。

在此基础上，研究人员开始设计滑模控制律，如公式（3）所示。

u=-αsgn（（x））-βs（x）-γ（x） （3）

式中：u为控制输入；α、β、γ为控制器的设计参数，这些参数决定了控制系统的响应速度以及稳定性。

电梯轿厢系统可以通过系统动态响应的要求以及工程实际经验，调节α、β、γ的具体数值，通过这种方式平衡控制性能，见表3。

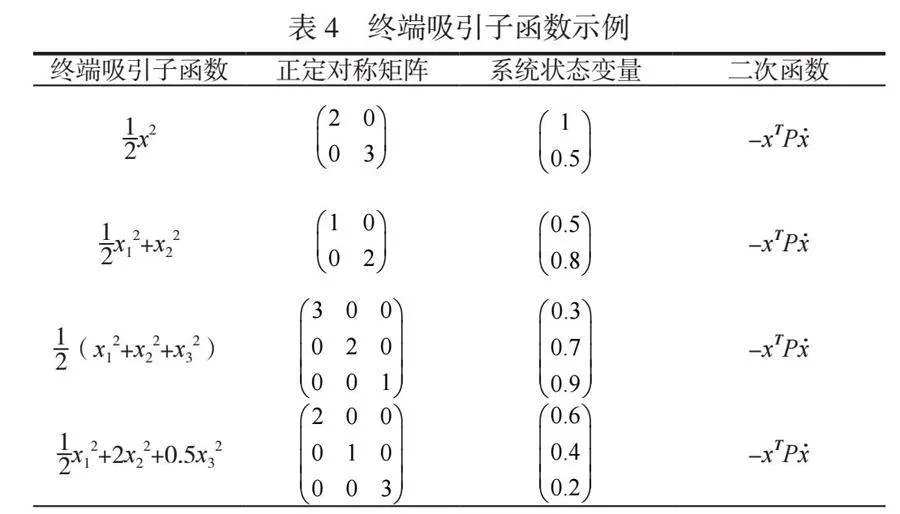
本次研究中，研究人员设终端吸引子函数为Vf（x），该函数的主要作用为确保系统状态在有限时间内收敛到滑模超曲面上。常见的选择是二次型函数形式，如公式（4）所示。

（4）

式中：P为正定对称矩阵；T为正宗对称矩阵，通过解Riccati方程确定。

这种设计不仅能够保证系统在有限时间内收敛，还能有效地抑制系统的震荡或者过渡过程中的振荡现象，从而提高控制系统的稳定性与精度。在电梯轿厢系统中，最优快速终端滑模控制器的应用具体体现在对轿厢水平振动的控制。通过实时测量并反馈系统状态，控制器基于预定义的滑模超曲面以及终端吸引子函数进行调节，见表4。

2.2 随机惯性权重粒子群算法对终端滑模控制器的优化

随机惯性权重粒子群算法（SIWPSO）是一种源于群体智能理论的优化技术，它借鉴了鸟群觅食的协作模式，通过群体中个体的协同与信息流通，不断探索并逼近问题的最佳解决方案。与传统的粒子群优化算法（PSO）相比，SIWPSO引入了随机惯性权重的概念，这一权重在算法迭代期间动态地调整其值，旨在实现全局搜索与局部搜索能力之间的精妙平衡，进而加速算法的搜索进程并提升其收敛效率[4]。在SIWPSO框架下，每个粒子均象征问题空间内的一个潜在候选解，而粒子的位置与速度则分别映射问题的可能答案及其探索路径。随机惯性权重的引入，赋予了粒子在搜索旅程中根据自身过往经验及同伴信息动态调整飞行轨迹的能力，这种灵活的自适应策略极大地增强了算法跳出局部最优陷阱的能力，为全局最优解的发掘开辟了更广阔的路径。

本次研究中，TSMC的参数需要被编码为粒子群的初始解。这通常涉及将连续参数映射到算法可以处理的离散或连续解空间中[5]。编码方式可以采用实数编码，其中每个参数直接对应粒子位置向量的一个维度。研究人员选择轿厢系统水平振动的性能指标作为适应度函数，该指标综合考虑了轿厢的位移以及控制器输出，该函数越小，说明系统的振动幅度以及控制能量消耗越低，控制性能越好。研究人员将种群规模设为50，同时将惯性权重设定在[0.4，0.9]随机取值，通过这种方式平衡算法的探索与开发能力，将最大迭代次数设为1000，确保算法有足够的时间进行搜索[6]。其优化步骤如下。1）对粒子群进行初始化。在这个过程中，系统在解空间中随机生成一定数量的粒子。每个粒子的位置代表一个潜在的参数组合，这些参数组合将用于后续的优化过程。为了确保粒子群的多样性，将每个粒子的速度初始化为≤0的随机值，这样可以避免粒子在初始阶段过于集中，从而影响优化效果。2）计算每个粒子的适应度值。将每个粒子的位置解码为一组控制参数。然后将这些参数融入轿厢系统水平振动的模型中。通过模拟或实际运行来评估这些控制参数对系统振动控制效果的影响。根据评估结果，计算每个粒子的适应度值。3）更新个体最优解以及全局最优解。如果当前适应度值更优，即表示当前参数组合的控制效果更好，那么更新该粒子的个体最优解。如果存在更优的个体最优解，即表示有某个参数组合的控制效果超过了当前的全局最优解，那么更新全局最优解。通过这种方式确保全局最优解始终代表当前最优的参数组合。4）在更新了个体最优解和全局最优解后，根据速度更新公式更新粒子的速度与位置。通过这种方式，确保粒子在解空间中朝更优的方向移动。然后，根据更新后的速度，调整每个粒子的位置。粒子群就能在解空间中不断探索，寻找更优的参数组合。5）在每次迭代完成后，检查是否达到了预设的最大迭代次数。如果没有达到，就返回步骤二，继续进行下一轮迭代。通过不断重复这个过程，粒子群能够在解空间中不断探索，逐渐逼近最优解。如果达到了最大迭代次数，就输出全局最优解，即最优的控制参数组合。这个最优解代表了在当前条件下能够达到的最佳控制效果。

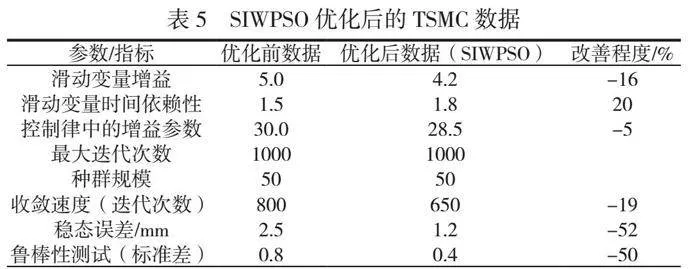
通过迭代优化，SIWPSO算法能够有效地找到最优或近似最优的控制参数，从而提高轿厢系统水平振动的控制性能，见表5[7]。

分析表5可以发现，优化后收敛速度提高，迭代次数减少，说明算法更快地找到了最优解[8]。在稳态误差方面，优化后稳态误差显著降低，说明系统更精确。在鲁棒性测试方面，优化后鲁棒性提高，标准差减小。

3 结语

本次研究中，工作人员构建轿厢系统水平振动的主动控制模型，明确了被控性能指标，通过构建轿厢系统水平振动的主动控制模型，为后续控制器的设计提供了精确的数学基础。该模型充分考虑了系统的不确定性以及外部干扰，为控制策略的制定提供了保障。在最优快速终端滑模控制器的设计中，研究人员提出了非奇异终端滑模控制器的设计方法。该控制器能够在有限时间内使系统状态达到期望的滑动面，并保证系统在滑动面上的稳定运动。非奇异特性确保了控制过程中不会出现奇异性问题，从而提高了控制器的可靠性。

参考文献

[1]陈岁繁，杨松，李其朋.基于BP-NSGA-Ⅱ优化的高速电梯轿厢水平振动变论域模糊PID控制[J].噪声与振动控制，2024，44（2）：63-69，81.

[2]谢伟平，朱铭超，尹一哲，等.电梯轿厢-导轨耦合作用下诱发的振动与二次噪声研究[J].噪声与振动控制，2023，43（4）：74-81.

[3]麻航飞，何伟，慕亚亚，等.高速电梯轿厢的水平减振设计及其优化[J].陕西科技大学学报，2022，40（6）：140-149.

[4]李泽华，柴铮，赵春晖.基于轿厢加速度解析的电梯运行健康度评价[J].控制工程，2021，28（10）：1909-1916.

[5]汪旭东，孙伟翔，许孝卓，等.直驱多轿厢电梯系统的调度控制策略[J].武汉大学学报（工学版），2019，52（8）：716-721，728.

[6]张瑞军，司鑫鑫，杨围围，等.随机参数高速电梯轿厢系统共振可靠性灵敏度研究[J].振动与冲击，2015，34（6）：84-88.

[7]薛金莲，冯永慧，吴惠兴.基于广义预测PID的高速电梯水平振动主动控制研究[J].机械科学与技术，2012，31（8）：1222-1226.

[8]杜小强，梅德庆，陈子辰.高速曳引电梯时变元模型与水平振动响应分析[J].浙江大学学报（工学版），2009，43（1）：148-152.