基于遗传算法的煤矿梭车转向机构优化策略探究

摘 要：为了提高煤矿梭车的灵活性，需要对其转向机构进行优化。本文以降低转弯直径和转弯阻力矩为目标，建立了目标函数，并对函数进行归一化处理。运用遗传算法对目标函数进行寻优计算，在兼顾转弯阻力矩和转弯直径的条件下，求解主销中心距的最佳取值，进而计算出其他结构参数的优化结果。比较结构优化前、后的控制目标，转弯直径从13.12m降至10.9m，转弯阻力矩从1.774×107N·mm降至1.530×107N·mm。经过优化设计，煤矿梭车的转弯直径和阻力矩均显著下降，达到了改进目标。

关键词：遗传算法；煤矿梭车；转向机构

中图分类号：TD 525 " " " 文献标志码：A

煤矿梭车的用途为井下煤炭转运，由于煤矿井下空间较小，对梭车转向机构的灵活性提出了较高要求，因此，在梭车转向机构优化设计阶段，需要着重提升其转弯性能。该设备在煤矿开采中具有重要应用，因此对其转向机构的研究比较广泛。任晓力[1]分析了煤矿梭车转向杆系的刚柔耦合作用机制。陈庆贺[2]对煤矿梭车的梯形转向机构进行了较深入的研究。张卫东[3]对煤矿无轨胶轮车的转向机构进行优化设计，并且验证了设计方案的有效性。

本文以TY9FB型煤矿梭车为分析对象，转向机构的优化目标为降低转弯时的阻力矩和转弯直径，以提高其灵活性。因此需要建立最小转弯直径和最小转弯阻力矩的目标函数，运用遗传算法进行寻优计算，求解目标函数最小值对应的转向机构结构参数。

1 基于遗传算法的煤矿梭车转向机构优化策略

TY9FB型煤矿梭车属于无轨胶轮车，其转向机构由车轮、下转向臂、横拉杆、转向块、纵拉杆、上转向臂、同步轴、车轴以及转向液压缸组成。在优化梭车转向机构过程中，本文提出2个关键目标，其一为缩小转弯直径，其二为降低转向时的阻力矩。

1.1 构建煤矿梭车转向机构目标优化函数

1.1.1 最小转弯直径目标函数建立

煤矿井下空间较狭窄，降低煤矿梭车转向机构的转弯直径能够更好地适应井下空间的作业特点。根据转向机构的结构，可以建立最小转弯直径的目标函数，如公式（1）所示。

minD=min（L/sinαmax+B-K） （1）

式中：D为转弯直径（mm）；minD为转弯直径的最小值；L为煤矿梭车梯形转向结构的前、后轮轴距（mm）；B为梯形转向结构的左、右轮轴距（mm）；K为煤矿梭车的主销中心距（mm）；αmax为外侧车轮的最大转角（°）。

1.1.2 最小转弯阻力矩目标函数建立

1.1.2.1 基本假设

转弯阻力矩大小会影响转向机构的灵活性。为了降低建模复杂度，需要做出以下假设：车轮和路面的接触部位为圆形，并且该圆形的直径等于煤矿梭车轮胎的宽度；当车轮转向时，所受摩擦阻力分别为滚动摩擦阻力和滑动摩擦阻力；在车轮发生滚动时，摩擦力和轮边减速器可以产生力矩，从而影响车轮的转速；4个车轮承载的车架载荷完全相等。

1.1.2.2 最小转弯阻力矩目标函数

煤矿梭车转弯阻力矩为前、后轮阻力矩的合力矩，计算方法如公式（2）所示。

Mz=G（f1∙e+f2∙a） （2）

式中：Mz为整车的转弯阻力矩（N·mm）；G为煤矿梭车的整车质量，计算取值为2×105N；f1为路面与轮胎间的滚动摩擦系数，计算取值为0.04；f2为路面与车轮间的滑动摩擦系数，计算取值为0.70；e为主销偏移量（mm），e=0.5（B-K）；a为轮胎的当量半径（mm）。

参数a的计算方法如公式（3）所示。

（3）

式中：rz表示煤矿梭车轮胎的自由半径，计算取值为622.5mm；rj表示煤矿梭车轮胎的静力半径，计算取值为584.0mm。

将参数e和a的计算方法代入公式（2），可以得到最小转弯阻力矩目标函数，如公式（4）所示。

（4）

式中：minMz为整车转弯阻力矩最小值（N·mm）。

1.1.3 多目标函数归一化处理

在第1.1.2节中建立了2个目标函数，转向结构优化设计阶段需要综合考虑以上2个目标，形成多目标函数，并对多目标函数进行归一化处理。处理流程为目标函数无量纲处理→规范化处理→归一化处理。以公式（1）和公式（4）为基础，其中的已知变量见表1。可见，对最小转弯阻力矩和最小转弯直径2个目标函数来说，未知变量仅为参数K。经过归一化处理，可以将包括最小转弯阻力矩和最小转弯直径的多目标函数转化为公式（5）。

（5）

式中：K的取值范围为1879mm～2513.8mm；F为经过归一化处理的目标函数。

1.2 基于遗传算法的多目标函数寻优计算

1.2.1 遗传算法编写

第1.1.3小节建立了煤矿梭车转向机构多目标优化函数，需要根据转弯阻力矩和转弯直径的控制目标对该函数进行求解。由于该问题较复杂，涉及2个不同的控制目标，因此引入遗传算法，利用大量的迭代运算完成目标函数寻优计算，实施要点如下所示。1）编写M文件。本文将MATLAB软件作为遗传算法的运行环境。该软件不能直接识别目标函数，在运行之前，需要将目标函数编写为MATLAB软件可识别的M文件。创建M文件，将公式（5）以代码的形式写入该文件，保存为F.m。2）编写遗传算法，优化梭车转向机构的相关代码。根据梭车转向机构的优化目标，在MATLAB中编写程序代码，用于目标函数寻优计算。程序代码见表2。

1.2.2 遗传算法运行结果分析

1.2.2.1 多代遗传后种群个体的目标函数值分布

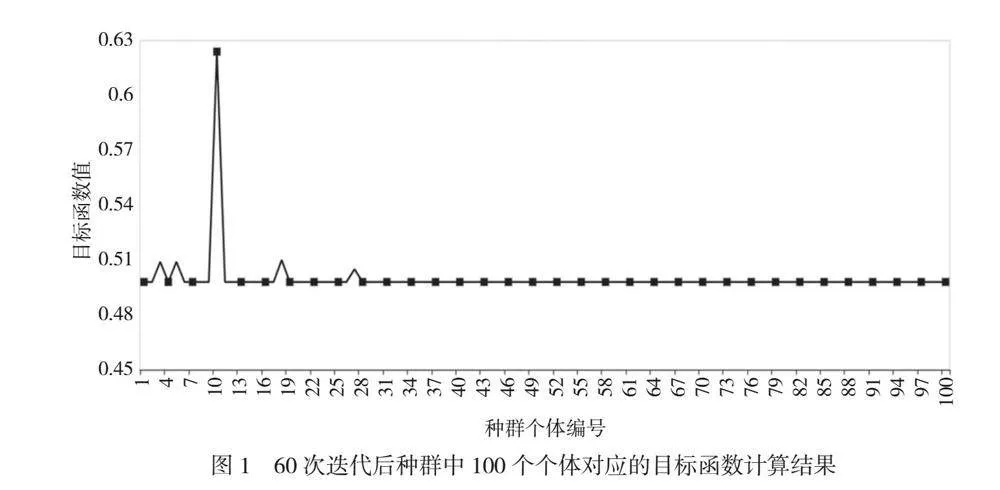
从程序代码可知，最大遗传代数为60代。经过60代遗传后，种群中100个个体对应的目标函数值如图1所示，即公式（5）的计算结果。由图1数据可知，种群经过60次迭代后，仅有部分个体的目标函数计算值较高，分别为0.509、0.508、0.624、0.510和0.505，对应的个体编号为3、5、10、18和27。剩余个体的目标函数计算值均达到稳定状态，计算结果为0.498。目标函数寻优计算旨在求出其最小值，由数据可知，虽然部分个体并未达到最小值，但是种群中的绝大部分个体均取得了最优解[4]。异常个体的出现与种群的变异相关，属于正常现象[5]。因此，经过60次迭代运算后，遗传算法能够有效求解出目标函数的最优解。

1.2.2.2 不同迭代次数对应的目标函数最优值

为了观察算法的收敛情况，在种群的60代遗传过程中，记录每一代遗传对应的最小目标函数值，将其作为对应迭代次数的最优值，进而绘制出目标函数最优值随迭代次数的变化趋势，结果如图2所示。由图2数据可知，在前8次迭代中，目标函数值快速下降。当迭代次数为8～13时，目标函数值继续下降，但是降幅非常小。当迭代次数超过13次时，目标函数值达到稳定，此时遗传算法完成收敛。

1.2.2.3 不同个体对应的目标函数均值

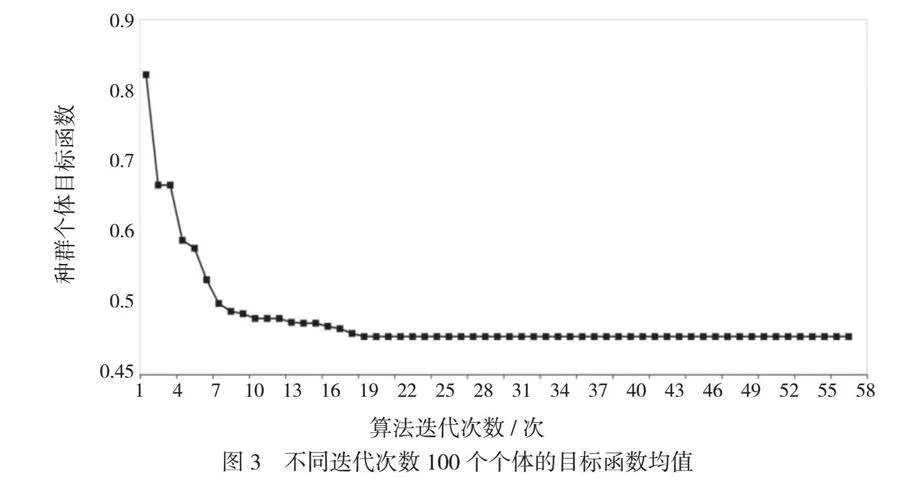
图2反映了每一次迭代中，100个个体对应目标函数值的最小值，但是不能体现种群中其他个体的目标函数计算结果。因此，需要统计60次迭代过程中，100个个体的目标函数计算结果均值，如图3所示。由图3数据可知，当迭代次数超过19次时，不同个体对应目标函数的均值达到稳定状态，其均值约为0.49。

1.2.2.4 目标函数优化结果

根据程序代码，经过60次迭代运算后，Y的输出结果为0.498，即目标函数F的最优值为0.498。此时，对应的种群为19。该种群对应的K值为2335.7mm。因此，在公式（5）中，主销中心距K的最佳取值为2335.7mm。与此同时，可计算出αmax=14.5。

2 煤矿梭车转向机构优化前、后效果对比

2.1 转向机构活塞杆行程优化前、后对比

由煤矿梭车转向机构的运行原理可知，当梭车进行转向操作时，液压缸中的活塞杆通过伸缩运动向其提供动力，活塞杆的行程大小与转弯动力、转弯直径密切相关[6]。活塞杆行程越小，转弯需要克服的阻力矩和转弯半径均越小。根据优化结果计算活塞杆的行程，并且与优化前的行程进行比较，结果见表3。由数据可知，结构优化之后，活塞杆行程大幅降低。

2.2 转向机构结构尺寸优化前、后对比

确定参数K的最优取值后，可以计算出煤矿梭车转向机构的结构尺寸，包括前轴轮轴距、左右轮轴距、主销中心距和内外侧车轮极限转角等[7]。煤矿梭车结构尺寸优化前、后的参数取值对比见表4。

2.3 转弯直径和转弯阻力矩优化前、后对比

将表4中的已知参数代入公式（1）和公式（4），计算结构优化前、后的转弯阻力矩和转弯直径。结构优化前的转弯直径为13.12m，结构优化后的转弯直径为10.9m，降幅为16.92%。结构优化前的转弯阻力矩值为1.774×107N·mm，结构优化后的转弯阻力矩值为1.530×107N·mm，降幅为13.75%。由此可见，利用遗传算法对转向机构进行优化后，煤矿梭车的转弯直径和转弯阻力矩均显著降低，达到了预期的优化目标。

3 结论

TY9FB型煤矿梭车是重要的煤矿开采设备，但是该设备在实际应用过程中缺乏足够的灵活性，难以适应井下的狭窄空间，需要对其转向机构进行优化设计。本文在优化设计中提出2项优化目标，分别为降低转弯直径和转弯阻力矩，据此建立函数，并且进行归一化处理，形成多目标优化函数。

目标函数建立之后，利用MATLAB软件搭建遗传算法的运行环境，对目标函数进行寻优计算，求解出主销中心距地最佳取值。再根据转向机构原理计算出其他结构参数的最优取值，包括转向臂长度、外侧车轮最大转角和内侧车轮最大转角等。

比较结构优化前、后的最小转弯直径和最小转弯阻力矩。最小转弯直径从13.12m降至10.9，降幅为16.92%。最小转弯阻力矩从1.774×107N·mm降至1.530×107N·mm，降幅为13.75%，均达到了优化目标。

参考文献

[1]任晓力.梭车转向杆系刚柔耦合分析[J].矿山机械，2024，52（5）：63-65.

[2]陈庆贺.矿用梭车用梯形转向机构研究及应用[J].矿山机械，2023，51（8）：74-77.

[3]张卫东.无轨胶轮车转向机构优化与验证[J].机械管理开发，2024，39（1）：162-163，166.

[4]马凯.基于同步缸技术的空间连杆转向机构设计[J].煤矿机电，2021，42（1）：38-40.

[5]任晓力.梭车转向机构的力学分析[J].煤炭技术，2020，39（3）：183-185.

[6]陆进添，刘丹，邓安田.剪叉式高空车转向机构结构分析[J].机械工程师，2020（3）：154-156.

[7]刘丹，邓安田，陆进添.高空车转向机构转弯半径优化设计[J].中国重型装备，2020（2）：20-22.