电气工程及其自动化中智能化技术的运用

摘 要：为研究智能化技术在电气工程及其自动化中的运用，并优化电气工程及其自动化领域的控制精度和动态响应性能，本文立足于智能化技术在电气工程及其自动化控制领域的特点，提出了一种以RBF神经网络为基础的模糊PID控制器。并通过MATLAB平台进行仿真试验证明。与传统的PID控制算法相比，该控制器具备更优秀的动态响应性能和控制精度，大幅降低了超调量，缩短了设定时间，并实现了控制参数在线自调整，为后续相关技术的发展奠定了坚实的理论与试验基础，并为智能化电气控制系统设计指明了新的方向。

关键词：电气工程；自动化；智能化技术

中图分类号：TM 76" " 文献标志码：A

在电气工程与自动化控制领域，由于智能化技术具有卓越的数据解析和整合能力，因此得到广泛应用。此类技术不仅使系统操作实现了自动化和便捷化，还具备高效的数据处理能力。在控制系统的设计与执行过程中，智能技术力求提升系统的适应性和精确度。为应对此挑战，众多研究者进行了深入研究。例如，刘甫等[1]在剖析传统比例-积分-微分（PID）控制算法局限性的基础上，针对无刷直流电动机控制问题，提出了一种具备模糊自适应功能的PID调节器。该调节器能根据操作条件的变化调整控制参数，从而提升无刷直流电动机的控制效能。此外，王立红[2]提出了神经网络模糊PID控制算法的架构，巧妙地将神经网络的强大学习能力与PID控制相结合，进行更精确的自动化控制参数调整，降低系统误差，从而提高系统控制精度。在此基础上，本文提出了一种径向基函数（RBF）神经网络模糊PID控制器，旨在提升电气工程自动化控制精度，通过精细调整控制策略应对复杂、多变的操作环境。

1 基本方法

1.1 PID控制原理

PID控制器是一种常见的线性反馈控制系统，其目的是调节输入信号以使参考信号rin（t）和系统输出信号yon（t） 间的控制偏差e（t）最小化，如公式（1）所示。

e（t）=rin（t）-yon（t） " （1）

PID控制策略运用比例（P）、积分（I）和微分（D）这3种控制作用叠加形成调节信号，对控制对象进行调节。比例增益（Kp）可实时调整系统偏差信号，减少偏差幅度。积分增益（Ki）能消除稳态工作条件下的残余误差，提高稳态精度。低Ki值可促进系统快速消除静态误差，但是过低可能会引发积分饱和现象。微分增益（Kd）可分析偏差信号变化趋势，预测未来走向，以提前介入系统调节，提高动态响应能力，缩短达到平衡点所需时间。

1.2 RBF神经网络

径向基函数（Radial Basis Function，RBF）神经网络具有结构简单且出色的逼近能力，在控制理论和实践领域中具有广泛运用。构建该网络时，为了在保证网络控制能力和运算效率间找到合适的折中方案，本文将一个3层的网络拓扑结构作为控制算法的核心。该3层结构包括输入层、隐含层以及输出层，如图1所示。

在图2中，输入层由一组含有n个元素的输入向量X={X1，X2，...，Xn}构成，它们代表神经网络的输入数据。隐含层包括一组高斯函数H={h1，h2，...，hn}，这些函数是激活函数，用于将输入向量映射到隐含层的空间。每个高斯函数与网络中的一个隐藏节点相对应。权值向量W={w1，w2，...，wn}包括从隐含层到输出层的连接权重，其中Wij代表连接第i个隐藏节点和第j个输出节点的权重。最终，输出层由这些加权求和后的输出值构成。

2 模糊神经网络PID控制器设计

现有研究表明，集成模糊PID调节技术与径向基函数（RBF）神经网络的控制策略越来越受重视。模糊PID控制器适应性强，但是优化动态响应有局限。RBF神经网络以自适应学习和近似复杂动态著称，可补充模糊PID的调节精度不足。本文提出基于RBF增强的模糊PID控制器，利用RBF自学习特性实时微调控制系统，以提高其性能。控制逻辑流程如图2所示。实施时，神经网络根据性能要求动态调整参数。同时，方法涉及即时处理驱动电动机速度和电流数据，以保证系统精确、高效并稳定运作。

根据图1和图2可知，RBF神经网络的结构化控制流程为输入层标准化模糊PID控制器输出，输送至隐含层并进行高斯核函数非线性转换和离散化处理，最终将非线性转换后的数据送至输出层进行加权和计算，进而输出控制参数。1） 在隐含层中，高斯函数如公式（2）所示。2） 在输出层，线性求和如公式（3）所示。3） PID变化量整定。

将RBF神经网络处理后计算出的参数变量直接传输至速度比例-积分-微分（PID）调节单元。在该调节环节中，根据神经网络处理得到的参数变量来设定控制器的输出参数，即∆kp、∆ki和∆kd。这些参数用于精确调节速度控制量，提升控制系统精度和响应性。为优化参数调整，本系统采用梯度下降法在线整定PID控制器参数。该方法可计算误差梯度并逐步调整参数，使误差最小化，更准确、高效地控制输出。整定过程如公式（4）所示。将计算得出的控制参数变量会与前一时刻的控制参数相结合，即将当前计算的参数与上一个时刻的参数相加得出最终调节结果。该最终结果将被反馈到系统中，用于调整控制变量，以更精确地进行变量控制，如公式（5）所示。

（2）

式中：C=[c1，c2，...，cn]为中心向量；b=[b1，b2，...，bn]为基款项量。

ym=ω1h1+ω2h2+...ωmhm （3）

式中：ω为网络权值。

（4）

式中：η为学习速率；等同于。

（5）

3 试验仿真

3.1 电机和控制系统仿真

本文利用MATLAB软件构建电机及其控制系统的仿真环境，旨在分析模糊神经网络PID控制器与传统PID控制器在控制性能上的差异。为了评估仿真中电机系统的动态响应特性，本文进行空载条件下的模拟驾驶试验。该试验采用的电动机模型参数设置如下：定子绕组电感为2.2 mH，电阻为0.324 Ω，电机具有2组对极，并且转动惯量为0.35 kg·m²。将模拟电机系统被施加200 V的电压，并在70 ms的持续时间内进行仿真。仿真结果如图3所示。

基于图3的仿真结果，电机绕组在无负载起动过程中的峰值电流为185 A，符合标准。正常操作下，绕组反电动势波形宽度约为125°，符合规范。这些数据表明本文构建的电机及其控制系统仿真模型具有高代表性，能提供稳定、可信的仿真信息。因此，该模型为控制策略开发和效能比较提供了有效仿真基础。

3.2 模糊神经网络PID算法仿真

设被控对象如公式（6）所示。

（6）

输入信号如公式（7）所示。

rin（t）=0.5sgn（sin（2πt）） " "（7）

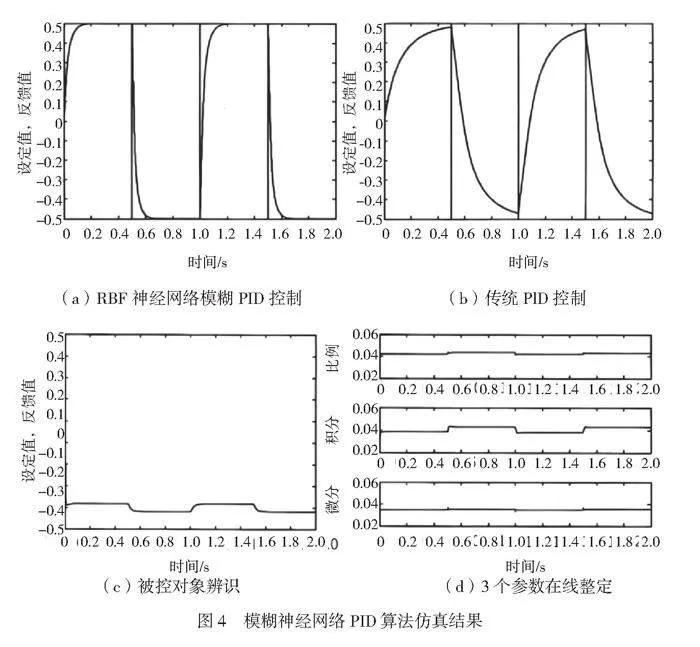
使用RBF神经网络进行系统辨识时，RBF神经网络的结构为3层，即输入层、隐含层和输出层。该网络结构为3-6-1，表明输入层具有3个神经元，隐含层具有6个神经元，输出层有1个神经元。该RBF网络的3个输入变量为u（t）、yout（t）和yout（t-1），输出为RBF网络辨识，其结果如图4所示。

MATLAB仿真曲线分析表明，当RBF神经网络与模糊逻辑被整合应用于PID控制策略中时，与传统的PID控制方法相比，本文提出的控制策略具有明显优势，即控制过程中的超调更小，系统的响应时间显著减少。此外，该策略还实现了PID控制器中比例（P）、积分（I）和微分（D）这3个关键参数在线实时自调整，进一步表明模糊RBF神经网络控制器在处理复杂的自动化控制问题过程中具有优良的性能表现。

4 结语

智能化技术的应用提高了电气自动化控制的精确性和稳定性。本文提出的基于RBF神经网络的模糊PID控制器运用了先进的智能算法，满足了电气工程中精确控制的需求。试验仿真结果验证了模糊神经网络PID控制方法在处理复杂系统的调节速度与准确性方面比传统PID控制更具优势。因此，本文不仅扩展了智能化技术在自动化电气工程领域的应用，还为今后相关技术的研究奠定了理论与试验基础。

参考文献

[1]刘甫，曾国辉，黄勃，等.基于改进模糊控制的无刷直流电机控制系统[J].制造业自动化，2021，43（10）：64-67，118.

[2]王立红.直流调速系统神经模糊自适应控制器设计[J].机电工程技术，2021，50（4）：190-191，253.