基于力-热耦合仿真模型的切削引入残余应力形成规律研究

关键词：切削加工； 力-热耦合； 数值仿真； 正交试验； 表面残余应力

航空航天领域中常见的薄壁结构零件的制造高度重视加工精度，切削加工在其中具有不可替代的关键地位[1]。切削加工过程经常在多因素、多物理场耦合的复杂力热环境下进行，许多零件在切削加工刚结束时，尺寸精度各指标均合格，但经过一段时间的放置，其形状会发生明显的变化。其中最主要的原因就是在切削过程中，零件表面引入了残余应力，残余应力的释放导致了零件的变形[2]。

有限元方法是一种结合差分思想的离散化方法，广泛应用于复杂场计算的工程领域中[3]。许多学者将有限元方法应用于切削加工过程的研究[4]。切削过程的基本因素是切削力和热，也是目前研究的重点[5]。哈尔滨理工大学张全建[6]利用Deform-3D模拟软件对振动影响下的铣削力进行模拟仿真分析，并选择了最佳的切削参数。与此同时，许多研究者对切削过程中的热-力耦合问题进行研究。哈尔滨工业大学赵伟龙[7]基于仿真软件对7075-T651 铝合金的切削过程进行了数值模拟计算，研究了切削要素与切削热、切削应力、切削应变等之间的关系。孙会来等[8]介绍了热-力耦合的切削模型，仿真切削过程中不仅要考虑切削力对工件的弹性变形和塑性变形产生影响，也要考虑切削加工中产生的切削热对加工弹塑性变形产生的影响。刘国伟等[9]研究了切削在列车减速中的吸能应用，运用了数值仿真方法和仿真软件，研究了热-力耦合的切削式吸能过程中，吸能效果与切削速度（撞击速度）、切削宽度、切削深度等参数的关系。肖茂华等[10]介绍了解析的切削热计算方法，创新地运用量热法测量了不同工艺参数下刀具、工件和切屑在切削过程中分别带走的热量。

通过上述可知，目前有许多科学家对切削过程进行过数值模拟计算，并探究了切削参数与切削力、残余应力等之间的关系。但对于切削过程的仿真建模，大多数是利用一款通用仿真软件或专用仿真软件进行。通用仿真软件虽然仿真类型较多，但对于切削、焊接、热处理等过程仿真操作较复杂，专用仿真软件恰恰在这些方面仿真较为简单并且仿真结果更加准确。本文结合通用仿真软件和专用仿真软件的优点，利用AdvantEdge 建立了切削过程的力、热有限元分析模型，利用Abaqus 建立了切削残余应力有限元仿真模型，分析了切削过程中不同切削参数下切削力、表面温度、表面残余应力的变化趋势，进行了切削试验，得到了表面残余应力，利用极差分析法得到了最佳的切削参数，为航空航天领域的薄壁结构零件的高精度制造提供了理论基础。

1 材料的本构模型

材料的本构模型是构建有限元模型的前提条件，本构关系的精确与否直接关系到有限元仿真结果的准确性。塑性变形和弹性变形是金属材料的两种常见的主要变形方式，而本构模型描述了材料的变形性质和特性。对于某种具体材料，本构模型用一系列具有特定参数和形式的方程描述了材料的应变、应变率和温度这些材料行为间的关系。

式中，σˉ为米泽斯（Mises）流动应力，εˉ为等效应变，n 为应变硬化指数，εˉ̇ 为等效应变率，εˉ̇0 为参考应变率，参考值一般取1s-1，Tm为材料的熔点，Tr为室温，m为热敏感性。

本文从参考文献[12]中获取铝合金7050 的材料物理参数及J-C本构模型参数（见表1）。

在切削加工过程中，切屑的剧烈塑性变形通常都会造成较高的切削区域温度和应变速率的变化，力热物理场的耦合作用非常明显，引起材料应变增大。当金属材料应变大到一定程度，就会发生材料损伤，这时就要考虑材料的损伤模型，本文采用J-C 材料损伤模型，其表达式为

式中，εf 为失效（塑性）应变，σ* 为静水压力与等效应力的比值，ε̇* 为塑形应变率与参考应变率的比值，T* 为无量纲（量纲一）温度。

参考文献[13]给出了铝合金7050 的J-C失效模型的参数的数值（见表2）。

2 切削过程有限元仿真分析

2.1 切削参数设置

本文研究的切削加工过程所采用的工件材料为经过固溶处理与时效处理后的7050 铝合金厚板，采用的刀具是直径为20mm的双刃铣刀，材质为硬质合金。

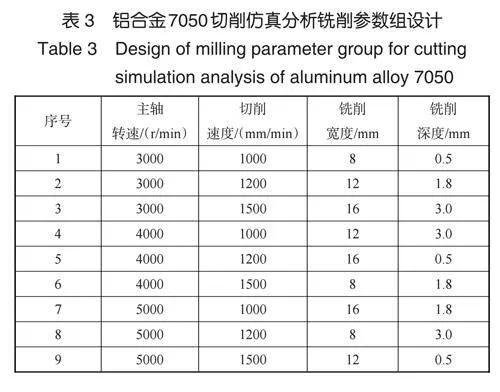
试验参数的设置采用了正交试验设计法，考虑了主轴转速、切削速度、铣削深度、铣削宽度4 个因素的三个水平得到9组正交试验参数，见表3[14]。

2.2 有限元建模

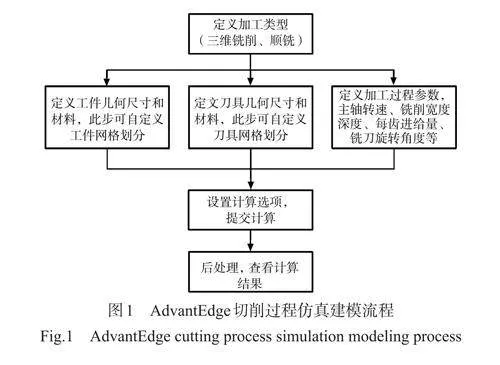
AdvantEdge 软件中的热-力耦合模块没有Abaqus 功能强大，但是Abaqus 用于切削仿真时，会经常遇到任务报错、单元畸变、不产生切屑、仅切到表面单元和切屑形态不理想等问题。因此，对切削过程的有限元仿真分为两步：（1）采用AdvantEdge 建立切削过程的力、热有限元分析模型，并计算出各组参数下的切削力、热情况；（2）将前一步得到的切削力、热结果经等效化处理后作为载荷施加在基于Abaqus 建立的切削残余应力有限元仿真模型上，并计算得到切削加工表面的残余应力分布情况（见图1）。

2.2.1 切削过程的仿真模型

本文通过AdvantEdge 有限元分析软件建立切削加工过程模型，在参数设置上将复杂的有限元模型参数序列转化为适应实际切削加工的切削参数序列[15]。根据实际切削加工中的切削参数输入软件即可，如刀具尺寸、主轴转速、切削速度、铣削深度、铣削宽度等。刀具和工件的几何模型尺寸、速度位移边界条件、局部网格划分及细化等参数采用默认设置。

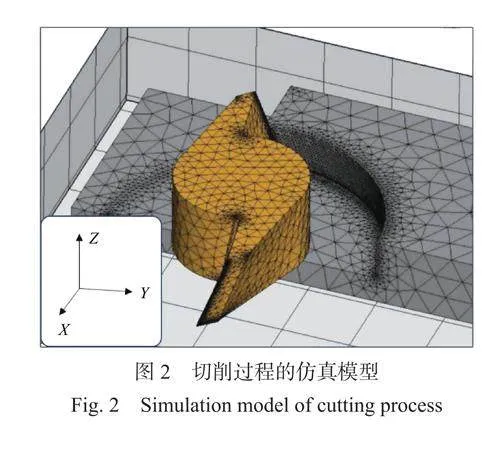
切削过程的绝大多数复杂的力-热耦合作用过程发生在刀具和工件接触处，在网格划分时应当在刀尖和工件接触处将两个实体对象的网格细化。最终，所建立切削过程的仿真模型如图2 所示。

2.2.2 表面残余应力的仿真模型

本文采用有限元仿真分析软件Abaqus 开展力-热耦合载荷对切削加工的表面残余应力研究，这也是残余应力仿真分析中常用的研究方式[16]。不同于 AdvantEdge，其可单独设置力载荷、热载荷或力-热耦合载荷，仿真分析不同力热载荷条件下的表面残余应力，建模灵活性更强，代价是在参数设置上比前者更为复杂。

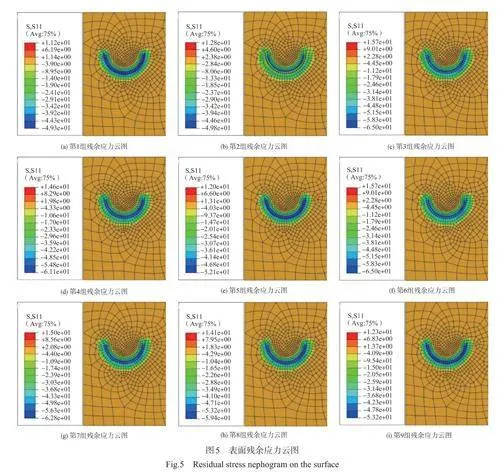
出于简化模型考虑，切削区域被设置成窄的半圆环形区域（实际的切削区域形状应为渐开线），切削力载荷是以将集中力施加在耦合了作用区域的参考点之上的方式定义的。参考点上施加的切削力载荷来源于AdvantEdge 的计算结果。

分析步骤分为两步，均设置温度-位移耦合，采用显示动力求解器。（1）时间设为0.005，在此步骤将切削力以瞬时的形式加载在参考点，将切削热以热边界条件形式按斜坡方式逐渐加载到切削区域中。（2）时间设为0.01，在此步骤将切削力以瞬时的形式卸载，将切削热以斜坡的形式卸载。网格采用C3D8T，初始室温为20℃。最终，所建立表面残余应力的仿真模型如图3所示。

3 切削加工仿真结果分析

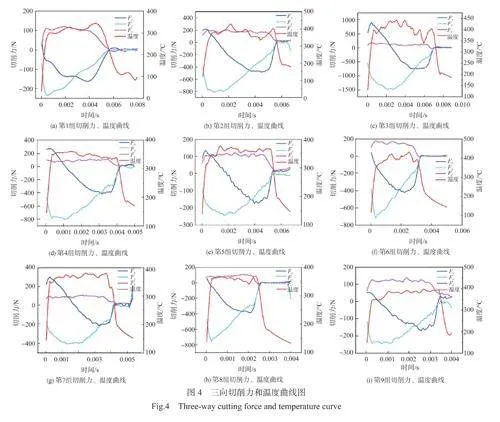
前文介绍了在AdvantEdge 中建立切削过程的仿真模型，在Abaqus 中建立表面残余应力的仿真模型。通过计算可得到三向切削力和温度曲线图，如图4 所示，得到表面残余应力云图，如图5 所示。接下来分别对切削过程中的三向切削力、温度以及表面残余应力进行分析。

3.1 切削力分析

由于切削力是变化的力，不是一个恒定的常量，因此要描述切削力的变化需要采用分段曲线或者将其等效为一个恒定的切削力，为了方便建模考虑，本文按照下式计算三个方向的力和等效切削力，结果如表4和图6所示。

式中，Fx，Fy，Fz 分别为Ｘ，Ｙ，Ｚ方向上的切削力，Fc 为等效切削力。

序号3 所对应的等效切削力最大，最大等效切削力为741.433N，此时，主轴转速为3000r/min，进给速度为1500mm/min，铣削宽度为16mm，铣削深度为3mm；序号9所对应的等效切削力最小，最大等效切削力为134.901N，此时，主轴转速为5000r/min，进给速度为1500mm/min，铣削宽度为12mm，铣削深度为0.5mm。

结果表明，三向力的大小变化趋势是基本相同的，X 和Y 方向上的切削力明显大于Z方向，这说明切削加工中切削力主要使切屑发生X-Y 平面上的剪切变形，后刀面对已加工表面的犁耕力占比相对较小。

3.2 表面温度分析

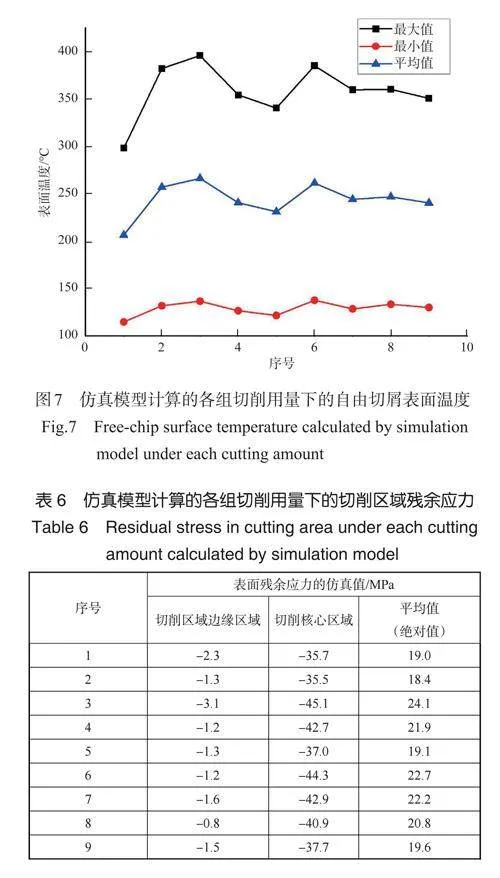
仿真模型计算得到的切削区域最高温度曲线是刀尖处的温度变化，不能反映切削区域的温度场变化，由于切削温度在实际测量时只能获取自由切屑的温度，为统一起见，提取了切屑的最高和最低温度，结果如表5 和图7 所示。其中，自由切屑表面温度的平均值最大为266.120℃，最小为206.307℃。

结果表明，仿真模型计算得到的自由切屑的表面温度具有和切削力相同的变化趋势，这说明切削力和切削热呈正相关，相同条件下，切削力越大则切削温度也越高。

3.3 表面残余应力分析

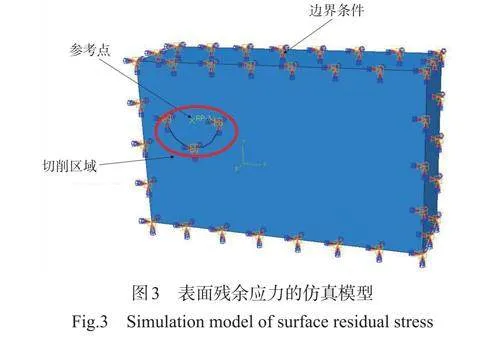
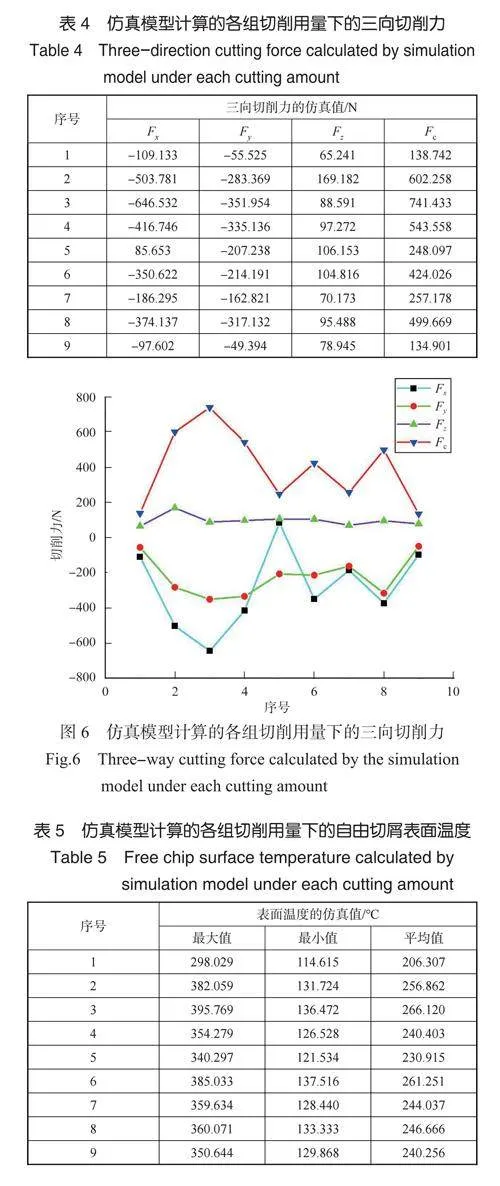
由图5 所示建立的残余应力仿真模型可以看到，残余应力在切削区域中的分布是不均匀的，从中提取切削核心区域和边缘区域的残余应力，并计算其平均值，结果如表 6和图8 所示。其中，表面残余应力平均值最大为24.1MPa，最小为18.4MPa。

结果表明，切削加工会在工件的加工表面引入残余拉应力，数值上大多为20～60MPa，符合铝合金7050 切削加工的一般经验，残余应力大小的变化趋势与切削力和热基本相同，这表明本文建立的残余应力仿真模型和切削力热仿真模型具有合理性和有效性。

4 切削过程试验验证

4.1 试验条件

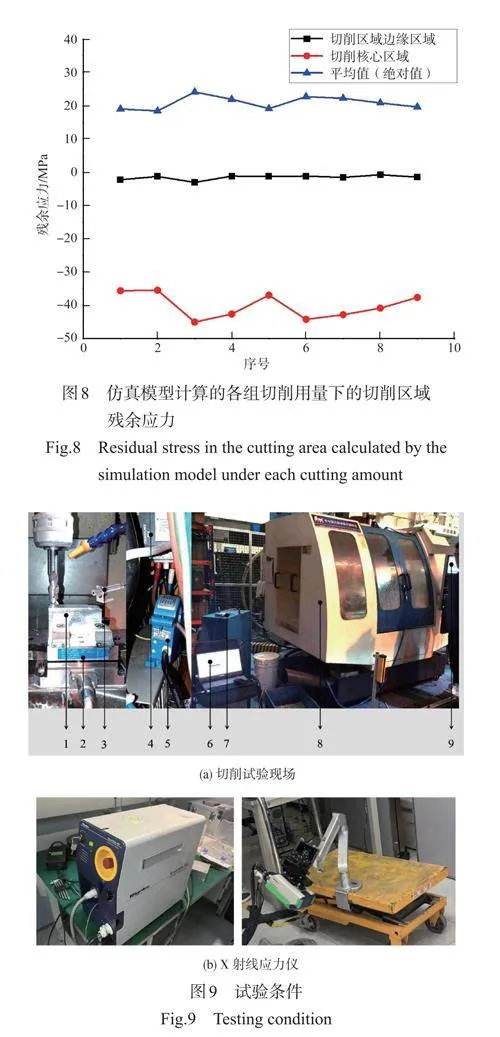
切削加工试验主要在配备了华中数控HNC-808DiM加工中心数控系统VMC850 立式加工中心上完成，试验用工件包括了材料为铝合金7050 的试验件。铝合金7050 试验件切削采用的刀具是直径为20mm的双刃硬质合金刀具，刀具的螺旋角为45°，铣削工况包括正铣和逆铣，分别进行多次，试验研究的铣削用量种类包括主轴转速、进给速度、铣削深度、铣削宽度，试验组别参数设计采用了正交试验法[17]，具体数据与有限元仿真分析中切削参数一致。试验中用来测试被加工块表面残余应力的设备为X射线应力仪，仪器型号为 Proto iXRD，如图9 所示。其中，1 为铝合金7050 工件、2 为Kistler 测力仪、3 为红外热传感器、4 为主轴电机驱动器、5 为霍尔电流传感器、6 为上位机、7 为模拟信号采集卡、8为加工中心、9为加工中心数控系统。

4.2 试验结果

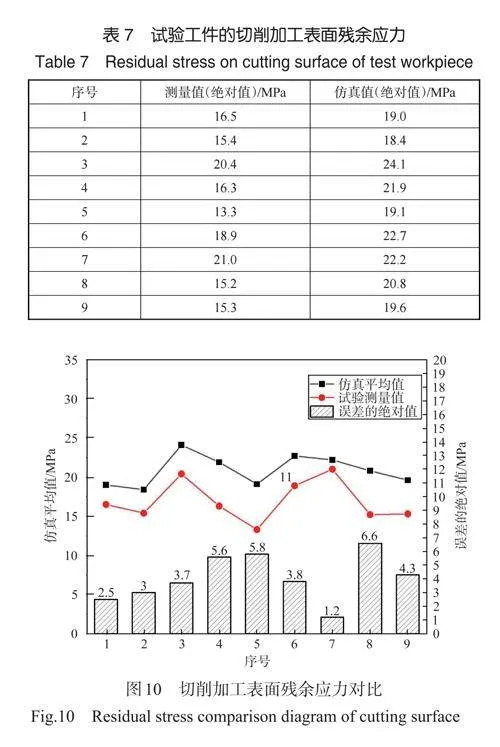
切削加工表面的残余应力是衡量切削加工质量的关键指标，表面残余应力对工件的表面质量、加工变形、疲劳寿命等有极大影响。本文采用 X 射线衍射法测量得到试验件表面残余应力，此处测量的残余应力与仿真分析中的表面残余应力方向一致，结果见表7。可知，序号7 所对应试验件的表面残余应力最大，最大值为21.0MPa。

4.3 误差分析

将第3 节中通过有限元建模分析得到的表面残余应力结果与第4 节通过试验得到的表面残余应力结果进行对比分析，计算得到他们的误差，结果如图10所示。

结果表明，第8 组误差的绝对值最大为6.6MPa，仿真数据为20.8MPa，试验数据为15.2MPa，这9 组试验数据误差的绝对值的平均值为4MPa。并且发现实测值普遍比仿真值偏小，由于技术上目前还很难实现对工件表面一定区域的表面残余应力场分布的测量，所以实际工件的表面无法确定最大残余应力位置，只能随机选取点测量，仿真模型表面的残余应力则手动选择了最大残余应力，因此导致了仿真值普遍大于实测值。虽然限于目前的残余应力测量技术，无法确定测量工件加工表面的残余应力分布，但从已有的随机选取的残余应力实测值和仿真模型的平均值上看，仍然能够在变化趋势上良好吻合，这说明本文建立的残余应力仿真模型具有良好的合理性。

4.4 结果分析与讨论

采用极差分析法对正交试验所得表面残余应力进行分析[18]，计算结果如表8 和图11所示。

结果表明，主轴转速、切削速度、铣削深度、铣削宽度的极差值分别为1.27、3.57、2.57、3.4，因此，铣削用量对表面残余应力的影响显著度从大到小排序为切削速度、铣削深度、铣削宽度、主轴转速。仅考虑最小表面残余应力的相对最优铣削用量为：进给速度为1200mm/min，铣削深度为0.5mm，铣削宽度为12mm，主轴转速为4000r/min。可用于指导生产实践。

切削加工过程是一种多变量、多因素、多物理场耦合的复杂过程，切削表面产生残余应力的因素也是多样的。本文重点考虑了切削速度、铣削深度、铣削宽度、主轴转速对引入残余应力形成的影响规律。由图4 可知，切削开始时，切削部位温度急剧升高，这是由铣刀与切削表面接触时产生大量摩擦热所导致的。此时，在切削部位就会发生高温、高压、高应变、高应变率的热-弹塑性变形，就会导致切削表面组织的浓度差，晶粒位向差发生改变，最终导致了表面残余应力的形成。

5 结论

本文基于切削加工过程进行了力-热耦合数值仿真分析，建立了切削材料的本构模型，建立了切削过程中的有限元模型，研究了切削过程中切削力、材料表面温度、材料表面残余应力的变化规律，通过切削过程试验验证了切削过程有限元分析的可靠性，通过试验数据分析得到了最佳的切削参数，其具体研究结论如下。

（1）在变化趋势上仿真结果与试验结果良好吻合，可利用该力-热耦合仿真模型预测7050 铝合金厚板切削引入残余应力的变化趋势。

（2）切削引入的残余应力与切削力、切削热呈正相关。切削速度对表面残余应力影响最大，铣削深度次之，切削宽度再次之，主轴转速最小。

（3）通过对切削参数的正交试验设计，并对正交试验所得表面残余应力进行极差分析，得到了使得固溶处理与时效处理后的7050 铝合金厚板表面残余应力最小的切削参数分别为：进给速度为1200mm/min，铣削深度为0.5mm，铣削宽度为12mm，主轴转速为4000r/min。

（4）切削开始时，切削部位温度急剧升高，导致切削表面产生剧烈的热-弹塑性变形，这是引起残余应力生产的主要原因。