汽轮机调速系统低频振荡特性与抑制策略研究

摘 要：本文研究汽轮机调速系统低频振荡特性与抑制策略，保证汽轮机调速系统的稳定性。分析汽轮机调速系统低频振荡的共振原理，探究其低频振荡特性；汽轮机调速系统控制模型，对低频振荡进行控制；基于改进蚁狮算法的GPSS参数优化流程，找出最优GPSS配置参数，便于从汽轮机调速侧快速抑制振荡。试验表明，该方法能够增强汽轮机调速系统阻尼特性，快速抑制转子角速度偏差幅度，提高汽轮机调速系统稳定性。

关键词：汽轮机；调速系统；低频振荡特性；抑制策略；蚁狮算法；GPSS配置

中图分类号：TM 712" " " " " 文献标志码：A

汽轮机调速系统出现低频振荡现象会危及整个运行机组的安全，影响系统工作。如果电力系统的稳定性遭到破坏，那么会导致一个甚至多个地区停电，影响人们的日常生活，也会对国民经济造成巨大损失[1]。低频振荡抑制策略始终都是研究人员的重点研究对象。在低频振荡机制中，负阻尼机制是最早提出的振荡原因，但是在实际应用中，负阻尼机制不能很好地解释低频振荡现象[2]。另一个低频振荡机制是当汽轮机调速系统固有的低频振荡频率和电力系统的自然振荡频率保持一致时引发的共振机制[3]。为此研究汽轮机调速系统低频振荡特性与抑制策略，在汽轮机调速系统中加装参数优化后的GPSS，增强阻尼特性，抑制低频振荡。

1 汽轮机调速系统低频振荡特性与抑制策略

1.1 低频振荡的共振机理

对于汽轮机调速系统来说，通过二阶经典模型表示发电机，在工作点处将转子运动方程线性化得到公式（1）。

KS∆δ+KD∆+2H∆=∆Pm " " " " （1）

式中：KS为同步力矩系数；∆δ为转子角偏移；KD为阻尼系数；H为转子惯性常数；∆Pm为机械功率变化。通过公式（1）即可计算出汽轮机调速系统的功率变化。

公式（1）不是非齐次微分方程而是二阶常系数方程，因此其有2种解，分别为通解与特解。其中通解所对应的解齐次方程的解，最终通解∆δ1（t）的计算过程如公式（2）所示。

（2）

式中：A0、φ0均可看作以初始条件所确定的积分常数；A0e-βt可以作为随着时间变化而产生的振幅；ω0为汽轮机调速系统无阻尼状态下自然振荡的角频率，ω02=；β为阻尼因子；t为汽轮机调速系统运行时间。

公式（1）的特解与机械功率变化∆Pm之间存在直接关系，最终特解∆δ1（t）的计算过程如公式（3）所示。

（3）

式中：r=2H；ω为汽轮机功率变化角频率。

通过计算公式（2）、公式（3）即可获得汽轮机调速系统的功率变化的通解与特解，最终轮机调速系统的阻尼为通解与特解之和，如公式（4）所示。

∆δ（t）=∆δ1（t）+∆δ2（t）" " " " " "（4）

当汽轮机调速系统的阻尼为正时，与阻尼有关的通解会有所衰弱，其余特解会出现等幅振荡的现象。如果汽轮机功率变化幅度与调速系统原有的低频振荡频率保持一致，会产生极大幅度的振荡，这种现象为共振机理的低频振荡[4]。

1.2 典型汽轮机调速系统模型

处于协调控制模式的汽轮机调速系统当进行一次调频时须通过协调控制系统与汽轮机数字电液控制系统协同完成，协调控制系统通过功率指令对功率回路进行补偿，而且功率补偿的部分不被速率所限制[5]。汽轮机调速系统控制模型如图1所示。

汽轮机调速系统使用三缸典型模型，调速系统各参数见表1。

表1 汽轮机调速系统参数

指标 参数 指标 参数

主控制器 1 一次调频的前馈系数K 1/0.3

速度控制系数s 0.06 高压缸蒸汽容积时间常数Thp 0.2s

中压缸蒸汽容积时间常数Fmp 7s 低压缸蒸汽容积时间常数Tlp 0.5s

高压缸功率比例Thp 0.3 中压缸功率比例Fmp 0.4

中压缸功率比例Tlp 0.3

当汽轮机调速系统控制模型切换开关处于位置1时，汽轮机调速系统处于“功率反馈”控制方式；当开关处于位置2时，汽轮机调速系统处于“阀位控制”控制方式；根据图1可知，当汽轮机调速系统中主控制器或回路发生故障时，控制系统将会产生振荡，若此时将开关切至位置2开启阀位控制，主控制器或回路会被汽轮机调速系统切除，不再参与汽轮机调速系统的控制，使汽轮机调速系统脱离低频振荡状态。由于典型汽轮机调速系统模型的控制方式稳定性较低，因此须在汽轮机调速系统调速侧安装稳定器。

1.3 基于改进ALO算法的GPSS设计

1.3.1 GPSS模型

GPSS模型是一种安装于汽轮机调速系统调速侧的稳定器，在GPSS模型中，将汽轮机调速系统的信号作为模型输入，通过GPSS稳定器完成汽轮机调速系统的相位补偿，将汽轮机调速其他的低频振荡转移至复平面的左面。GPSS模型的输入信号为-∆ω，GPSS模型的具体示意图如图2所示。

汽轮机调速系统是由预控制系统模块和执行模块组成的，Gcon（s）、Gact（s）为这2个模块的传递函数，配置GPSS稳定器后的汽轮机调速系统模型如图3所示。

将-∆ω输入配置GPSS稳定器后的汽轮机调速系统模型后，通过传递函数最终输出GPSS控制信号。

1.3.2 改进型蚁狮算法

为了解决蚁狮算法移动步幅较大以及多样性差的问题，对蚁狮算法进行改进，改进后的蚁狮算法通过蚁狮不断移动并挖掘陷阱，使蚂蚁落入陷阱中，并根据各陷阱捕食蚂蚁的数量不断调整陷阱位置，提高蚁狮算法挖掘的准确性与效率。为此，改进型蚁狮算法改进了适应因子I与蚁狮开发方式。

1.3.2.1 改进适应因子I

蚂蚁被蚁狮挖掘的陷阱捕食后，基于适应因子I的变化会缩小蚁狮的挖掘范围，适应因子I的约束条件如公式（5）所示。

（5）

式中：第t次迭代中适应因子I最小值为ct，最大值为dt，I=10w·（t/Z）。其中，Z为迭代次数的最大值，w为收缩因子。

在公式（6）的约束下，适应因子I的特性转变为分线段性，改进适应因子，如公式（6）所示。

（6）

式中：Rrand为[0，1]任意的自然数；将三角函数项代入公式（6）中，在改进型蚁狮算法持续迭代的过程中，在大于0且小于1的范围内，三角函数项整体呈上升趋势，而适应因子I也呈上升趋势，提高改进蚁狮算法的挖掘多样性与全局搜索能力。

1.3.2.2 蚁狮开发方式改进

改进蚁狮算法的挖掘后期，此时蚁狮所在位置与全局最优解应该非常接近，因此应该缩小蚁群的搜索步幅，提高搜索准确性。因此，在第t次迭代的RE'中加入反调因子，如公式（7）所示。

（7）

式中：Cm为最大循环次数。改进后的蚁狮搜索步幅在寻优过程中不断缩小，达到步长反向调节的效果，令GPSS寻优迭代后期各参数跳变范围缩小。

1.3.3 目标函数设计

在设计目标函数的过程中要对低频振荡模态的最小阻尼比进行约束，保证汽轮机调速系统的阻尼始终保持在一定水平上，因此将最小阻尼比ξmin=min{ξ1，ξ2，…，ξs}进行定义。将最小阻尼比ξmin的最大化作为目标函数，如公式（8）所示。

（8）

式中：s为各振荡模式的序号。将GPSS参数取值范围约束与目标函数相结合，获得的优化条件，如公式（9）所示。

（9）

1.3.4 改进蚁狮算法的GPSS参数优化流程

本文将改进蚁狮算法引入GPSS参数设计中，对GPSS参数进行优化，并对汽轮机调频系统进行仿真。采用改进蚁狮算法将GPSS稳定器参数进行优化，包括以下6个步骤。1）步骤一。初始化改进蚁狮算法的参数，根据蚁狮种群的规模与蚂蚁数量确定GPSS参数种群的规模，随机设定1组GPSS参数种群的初始解X={X1，X2，…，Xs}。2）步骤二。将汽轮机调速系统参数引入无穷大电网模型中，为使汽轮机调速系统产生低频振荡响应，在电网模型中增加5%的阶跃扰动。3）步骤三。通过Prong算法模态识别汽轮机调速系统的各种模式，提取汽轮机调速系统低频振荡时的特征值，并通过特征值计算低频振荡的阻尼比。4）步骤四。通过改进蚁狮算法进行寻优操作，不断更新获得下一代最优候选解X。5）步骤五。回到步骤二继续进行循环，直至达到迭代次数，停止循环。6）步骤六。输出最终最优GPSS配置参数以及相应的目标函数J。GPSS寻优的最终目的是获取能够符合汽轮机调速系统稳定性要求的配置方案，当调速系统出现低频振荡时，可以从汽轮机调速侧快速抑制振荡。

2 试验结果

该试验构建某火电厂汽轮机调速系统的仿真模型，验证了改进蚁狮算法优化GPSS参数方法的有效性。将蚁狮与蚂蚁种群规模设定为60，维数为3，最大迭代次数设定为200，并与常规蚁狮算法进行比较。

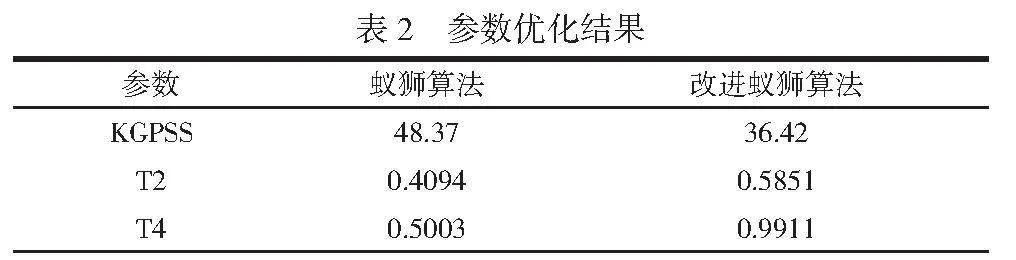
首先，优化参数，优化结果见表2。

表2 参数优化结果

参数 蚁狮算法 改进蚁狮算法

KGPSS 48.37 36.42

T2 0.4094 0.5851

T4 0.5003 0.9911

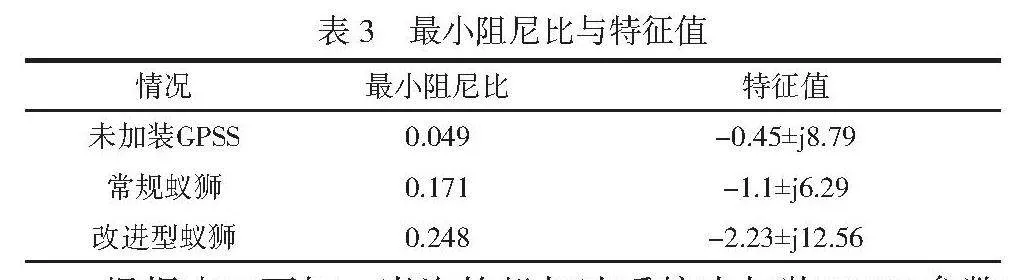
其次，在相同设置条件下，对未加装GPSS参数时、安装蚁狮优化的GPSS参数后以及安装改进型蚁狮优化的GPSS参数后的汽轮机调速系统进行比较，其最小阻尼比与特征值见表3。

表3 最小阻尼比与特征值

情况 最小阻尼比 特征值

未加装GPSS 0.049 -0.45±j8.79

常规蚁狮 0.171 -1.1±j6.29

改进型蚁狮 0.248 -2.23±j12.56

根据表3可知，当汽轮机加速系统未加装GPSS参数时，其振荡模式的最小阻尼比约0.049，此时，汽轮机加速系统处于弱阻尼状态。汽轮机加速系统安装常规蚁狮优化的GPSS参数后，其振荡模式的最小阻尼比有所增加，说明此时汽轮机加速系统的阻尼特性已提高；汽轮机加速系统加装改进型蚁狮优化的GPSS参数后，振荡模式的最小阻尼与未加装GPSS参数时相比增加了0.199，升至0.248，说明进一步改善了系统的阻尼特性，改进后的蚁狮算法寻优性更强。

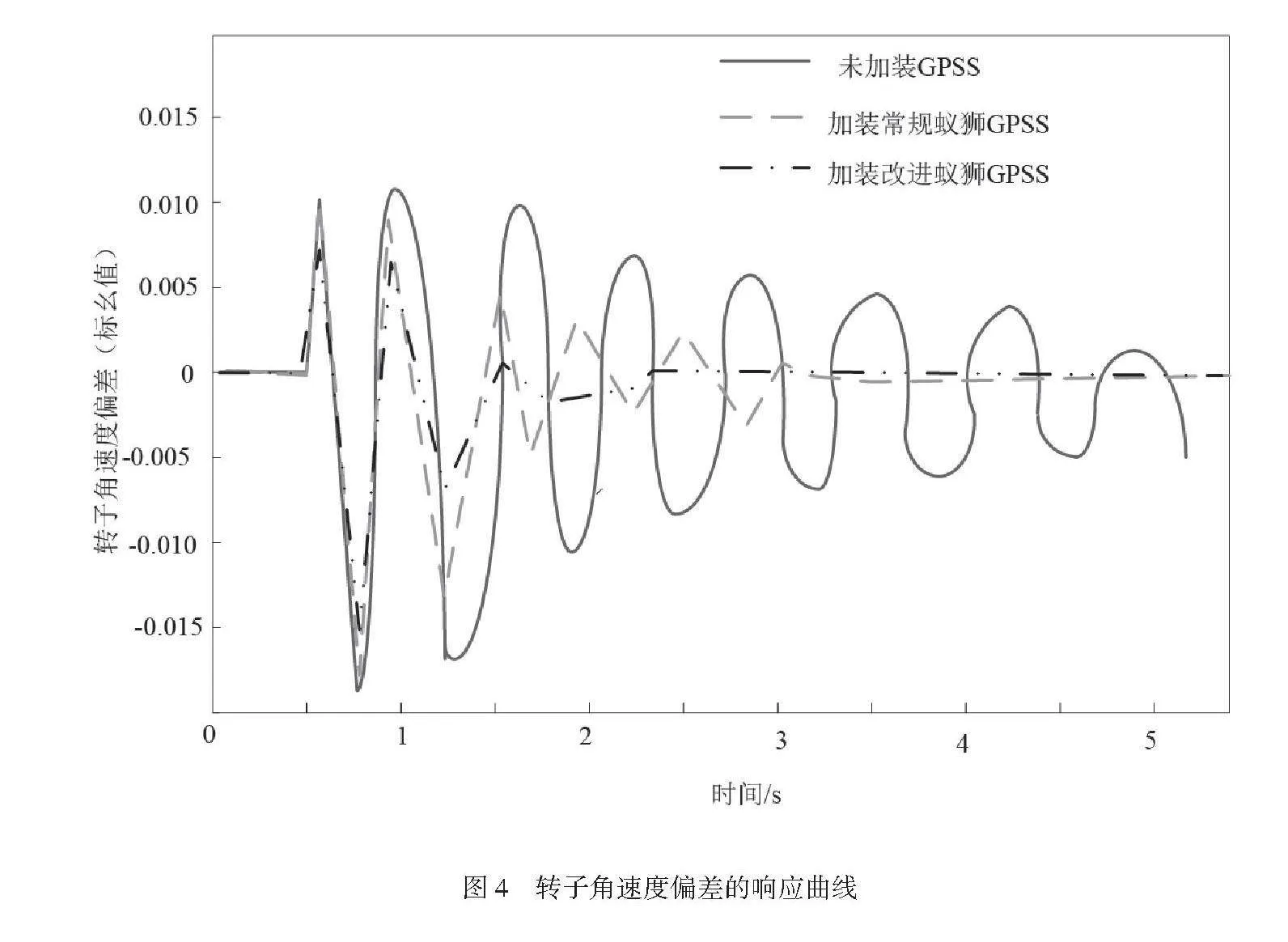
在汽轮机发电机励磁系统输入电压侧增加5%的阶跃扰动，扰动时间为0.2s。转子角速度偏差的响应曲线如图4所示。

根据图4可知，当未加装GPSS的汽轮机调速系统受到扰动时，出现低频振荡情况，并且转子角速度偏差波动较大，直至6s也未完全稳定；安装常规蚁狮优化的GPSS参数后，转子角速度偏差波动缩小，在3s左右趋于稳定，然而加装改进型蚁狮优化的GPSS参数后，汽轮机调速系统的稳定性更好，转子角速度偏差在2s左右趋于稳定。说明在汽轮机调速系统中加装改进型蚁狮优化的GPSS参数能够很好地抑制低频振荡情况。

3 结论

当汽轮机调速系统固有的低频振荡频率和汽轮机功率的变化频率相近时，会引发共振机理的低频振荡，如果不及时抑制处理，就会影响汽轮机调速系统的稳定性。本文将未加装GPSS、安装常规蚁狮优化的GPSS参数后加装改进型蚁狮优化的GPSS参数后的汽轮机调速系统进行比较，对比三者的阻尼特性，试验结果显示，未加装GPSS参数时的最小阻尼比为0.049，安装常规蚁狮优化GPSS参数后的最小阻尼比为0.171，加装改进型蚁狮优化的GPSS参数后的最小阻尼比为0.248，说明本文方法的阻尼特性好。

参考文献

[1]谢昌亚，朱龙飞，胡娱欧，等.660MW超临界火电机组汽轮机及其调速系统精细化模型研究和应用[J].热能动力工程，2023，38（6）：58-67.

[2]易建波，张国洲，张鹏，等.超低频振荡阻尼控制中的水轮机调速系统参数双层优化策略[J].电工技术学报，2022，37（5）：1219-1228.

[3]方日升，林耀东，徐振华，等.基于录波曲线的电力系统低频振荡事故原因分析与抑制策略[J].中国电力，2021，54（11）：104-114.

[4]熊鸿韬，汪宗恒，尚磊，等.一种用于电力系统低频振荡抑制的新能源电站阻尼注入控制器设计及特性分析[J].电网技术，2022，46（7）：2690-2700.

[5]冯鼎元，康英伟.汽轮机侧机网耦合系统低频振荡特性与抑制策略研究[J].河南科技大学学报（自然科学版），2022，43（3）：45-54，7.