煤矿井下的UWB定位基站布设优化研究

摘 要：为了克服煤矿井下复杂环境对超宽带（UWB）定位系统基站布设的影响，本研究引入了一种创新的自然启发式元启发算法——星鸦优化算法（NOA），旨在优化UWB定位系统的基站布局。本文以UWB基站布设的区域覆盖率作为优化的目标函数，并通过NOA的迭代过程，寻求最优的基站布局方案。仿真试验表明，NOA的收敛精度和收敛速度很高。研究结果表明，NOA在井下复杂环境中的UWB定位系统中的应用潜力很大，为进一步测试实际环境和算法优化提供了理论基础和实践指导。

关键词：UWB定位技术；星鸦优化算法；基站布设；煤矿井下；区域覆盖率

中图分类号：TN 914" " " " " 文献标志码：A

随着国家对煤矿安全和智能化建设的重视，煤矿井下定位系统面临新挑战，须在复杂的电磁干扰、多径和阴影效应环境中实现高准确性和高时效性定位[1]。传统的射频识别（RFID）、Wi-Fi、紫蜂无线通信网络（ZigBee）和蓝牙等技术在适应性、抗干扰性和传输距离等方面存在不足，难以满足高精度需求。超宽带（Ultra Wide Band，UWB）技术以其优越的抗干扰性和穿透能力，能够在井下复杂环境中进行高精度定位。然而，井下环境的复杂性对定位系统的设计和实施提出了挑战，特别是在基站布设优化方面。在煤矿井下环境中，布设UWB基站对定位精度有显著影响[2]。基站布设不当会导致定位误差增大，影响救援和监测工作的效果。因此，研究和开发一种高效的基站布设优化方法十分重要。本文提出了一种新型基站布设优化方法，将星鸦优化算法（Nutcracker Optimization Algorithm，NOA）应用于煤矿井下UWB定位系统。NOA是一种自然启发式元启发算法，其灵感来自克拉克的星鸦寻找食物的行为模式。本文利用NOA解决井下环境中的UWB基站布设问题，提高定位系统的精度和覆盖效率。

1 超宽带定位技术

1.1 UWB技术的基本原理

UWB技术是一种使用极宽频带传输电磁波的通信方式。UWB的主要特点是其频带宽度通常超过500 MHz，载波中心频率gt;2.5 GHz。这种特点赋予UWB多个优势，例如数据传输率高、功耗低以及穿透能力良好。UWB定位技术主要根据电磁信号的时间延迟测量来确定目标位置。与传统的窄带信号相比，UWB信号脉冲宽度短，时间分辨率高，定位系统精度更高。

1.2 UWB定位算法

到达时间差（Time Difference of Arrival， TDOA）是一种广泛应用于UWB定位系统的方法。TDOA基于从不同基站接收的信号时间差来确定目标位置。具体来说，至少需要3个基站来形成一个TDOA定位系统。每个基站测量信号到达时间，并将这些信息发送至中央处理器，如图1所示。图1有3个基站，基站一作为基准基站且已知3个基站的坐标位置，（x1，y1）、（x2，y2）和（x3，y3）分别为基站一、基站二、基站三的位置坐标；（x，y）为所求标签点的未知位置坐标。计算信号从目标到达每个基站的时间差，再根据距离差构建双曲线方程，如公式（1）、公式（2）所示。

（1）

（2）

式中：di为标签与第i个基站的距离，i=1，2，3，...，n；D21为标签到第二个参考基站与基站一之间的距离差值；D31为标签到第三个参考基站与基站一之间的距离差值；T1、T2和T3分别为标签的电磁波信号到达基站一、基站二和基站三的参考时间；c为电磁波的传播速度。利用Chan算法求解该非线性方程组就可以得到标签坐标位置（x，y）的数值。

1.3 煤矿井下环境对定位系统的影响

煤矿井下环境给UWB系统带来了多重挑战。井下封闭空间以及物理障碍（例如岩石、煤层和支撑结构）导致信号反射和衰减，影响定位精度。UWB信号具有高频特性，尽管UWB的高时间分辨率有助于抵抗多径干扰，但是井下环境的显著多径效应（反射、衍射和散射）影响了定位精度，井下电气设备产生的电磁噪声也可能干扰UWB信号。因此，UWB技术理论上适用于井下定位，其实际应用须考虑这些井下特有因素。在UWB定位系统的设计中，优化基站布设和信号处理至关重要，以保证其在特殊环境下的性能。

2 NOA算法

2.1 算法描述

NOA是由Mohamed Abdel-Basset 等[3]在2023年提出的一种新型的自然启发式元启发算法，其灵感来自克拉克星鸦的行为模式。克拉克星鸦以其独特的食物寻找和储藏策略而闻名。这种策略包括在广阔区域内寻找食物并将其储存于地面不同的位置，以备不时之需。NOA将这种行为模式抽象化并应用于解决复杂的优化问题。

NOA的核心思想是通过模拟星鸦在不同季节的行为来寻找全局最优解。在夏季和秋季，星鸦将食物储藏于不同地点，这相当于在解空间中探索多个潜在的解决方案。在冬季和春季，星鸦通过回忆以前储藏食物的地点来寻找食物，这相当于在已探索的解空间中寻找最优解。

2.2 算法设计

在NOA中，笔者基于上述2个主要行为来模拟星鸦的行为，主要包括以下2种策略。1）觅食和储存策略（Foraging and storage strategy）。2）缓存搜索和找回策略（Cache-search and recovery strategy）。在2种策略中，星鸦种群均存在勘探（Exploration）和开发（Exploitation）行为，即每种策略又包括2种不同的种群行为。

2.2.1 种群初始化

与大部分智能优化算法一样，NOA的种群初始化也是在问题的搜索空间中随机产生星鸦个体。假设种群规模为 N，问题维度为 D，那么初始化过程如公式（3）所示。

=（-）·+ （3）

式中：为第t代星鸦个体的第j维变量；i为基站个数，i=1，2，…，N；j为像素点个数，j=1，2，…，D；、分别为第j维变量的上界和下界；为[0，1]的随机向量。

2.2.2 觅食和储存策略

一群星鸦寻找食物的储存空间，以松树种子为代表，星鸦将发现的松树种子储存在适当的贮藏处，该机制可分为觅食和储存2个主要阶段。

第一阶段勘探，如公式（4）、公式（5）所示。

（4）

（5）

第一阶段开发，如公式（6）所示。

（6）

式中：为第t次迭代的一个新位置；为第t+1代第i个星鸦个体的最新位置；Xt i，j为第t代第i个星鸦个体的第j个位置；Xt m，j为当前种群在第t次迭代中所有解的第j维均值；Xt A，j、Xt B，j和Xt C，j为从种群中随机选择的3个不同的星鸦个体，作为指标探索高质量的食物来源；Lj、Uj为第j维的上界和下界；γ为根据Levy飞行函数生成的随机数；为当前种群的最优个体，、为从种群中随机选择的2个不同的星鸦个体；τ1、τ2和τ3，r1、r2和r3均为[0.1]的随机数；τ4为一个服从正态分布的随机数；τ5为一个Levy飞行函数生成的随机数；μ为基于τ3、τ4和τ5生成的数；Tmax为最大迭代次数；t为当前迭代次数；δ设为0.05；l为从1线性减至0的衰减因子，以提升算法的多样性。

觅食与储存策略的计算流程如图2所示。

2.2.3 缓存搜索和找回策略

当冬天来临时，星鸦从觅食和贮藏模式转变为搜寻和回收模式，开始寻觅它们之前储存的食物。这个阶段称为第二次探索。星鸦使用空间记忆策略来定位它们的贮藏物。基于星鸦个体的 2 个参考点（Reference Points，RPs）进行缓存搜索和找回策略。为了记住储存食物的位置，星鸦选择了2个参考点。2个参考点的计算过程如公式（7）～公式（10）所示。

（7）

（8）

（9）

（10）

式中：为当前代t中第i个星鸦的第一个缓存参考点；为当前代t中第i个星鸦的第二个缓存参考点；RP为一个随机位位置；Prp为概率，其作用是确定在搜索空间内全局探索其他区域的百分比；为优化问题中第二维的上界；、分别为所求解参数的的上界和下界；θ为[0，π]的随机弧度；为[0，1]的随机向量；α为保证NOA定期收敛所确定的值。

最开始的参考位置可以根据公式（3）得到。如果星鸦不能找到第一个参考点RPti，1储存的食物，那么它将通过第二个参考点RPti，2识别它。第一个参考点是通过更新相邻区域内的当前位置来找到星鸦周围隐藏的缓存来生成的，第二个参考点是通过在问题的搜索空间内更新当前解决方案来生成的，以帮助星鸦搜索储藏的食物。

第二阶段勘探，如公式（11）～公式（13）所示。

（11）

（12）

（13）

式中：Xt+1 i，j为第t+1代第i个星鸦个体的第j个位置；Xt best，t为第t次迭代中第j维的最佳位置；Xj c，t为从种群中随机选择的星鸦个体位置；Eq·（11）为记住了食物隐藏存储位置的星鸦个体，返回公式（11）继续迭代；Eq·（12）为没有记住食物隐藏存储位置的星鸦个体，返回公式（12）继续迭代。

第二阶段开发，如公式（14）～公式（16）所示。

（14）

（15）

（16）

式中：f（）为目标函数f当星鸦个体位于时的值；f（）

为目标函数f当位于参考点一时的值；f（）为目标函数f当位于参考点二时的值；Eq·（14）、Eq·（15）为如果满足相应条件则返回公式（14）、公式（15）进行计算；公式（14）为指导NOA在第一个参考点周围最有希望的位置，如果没有得到预期结果，那么它将在其他区域继续探索；公式（15）为指导NOA在第二个参考点周围最有希望的位置，如果没有得到预期结果，那么它将在其他区域继续探索；公式（16）为第一个参考点与第二个参考点的探索行为之间的权衡。

缓存搜索和找回策略的计算流程如图3所示。

2.3 基于NOA求解基站最优布设

NOA求解最优基站布设的具体步骤如下。步骤一是种群初始化。随机生成初始基站位置，作为NOA中“星鸦”的初始位置集合。步骤二是食物储藏（全局搜索）。模拟星鸦储藏食物的行为，在解空间内探索新的基站位置。步骤三是食物寻找（局部搜索）。模拟星鸦寻找食物的行为，根据已有的最优解和其他星鸦的位置信息来更新当前解。步骤四是适应度评估。对每个个体基于目标函数计算其适应度值，以此确定每个个体的最佳适应度以及整个种群中的最优适应度。步骤五是更新解集。根据适应度评估结果，选择性能更优的基站布设作为新一轮迭代的候选解。步骤六是迭代过程。重复步骤二至步骤五，直到达到预定的迭代次数或解的质量阈值。从迭代过程中选择性能最优的基站布设位置作为最终解。

由于其独特的搜索策略和多目标优化能力，因此NOA非常适合应用于煤矿井下UWB定位基站的布设优化。由于NOA 具有多样性和适应复杂问题的特性，因此其可以在大规模解空间中找最优解。，尤其是在井下这种复杂和动态变化的环境中。在平衡全局探索和局部开发方面，NOA提供了一种有效的方法来处理定位系统中的基站布设问题，特别是当面对多个目标和多种约束时。因此，NOA不仅适合理论研究，而且具有实际应用于煤矿井下UWB定位系统优化布设的潜力。随着进一步研究，NOA在煤矿井下安全和效率方面的应用前景将更广阔。

3 仿真试验

3.1 基站布设优化指标

在UWB基站布设中，三维位置精度稀释因子（PDOP）与区域覆盖率是2个关键因素。根据PDOP衡量基站在空间中的相对布设对定位精度的影响。在定位系统中，目前普遍使用几何精度稀释因子（GDOP）衡量基站几何布设对定位精度的影响程度[4]。在UWB定位系统中，基于TDOA信息的位置估计方法一般都校准了时间偏移误差，因此GDOP应替换为PDOP。PDOP越小，基站几何结构分布越均匀，性能越好； PDOP 越大，基站几何布设越差。当PDOP较低时可以获取更高的定位精度，当PDOP﹤3时，说明基站几何结构较好。PDOP的计算过程如公式（17）所示。

（17）

式中：HDOP为水平分量精度因子；VDOP为垂直分量精度因子。

区域覆盖率关注基站能覆盖的空间范围，保证整个目标区域内均有稳定的信号覆盖。目前已有许多研究关注PDOP对UWB基站布设优化的影响，本文将重点利用NOA仿真试验确定基站位置，保证基站信号能有效覆盖整个目标区域。

3.2 覆盖模型

假设煤矿井下巷道宽6 m，高4 m，长100 m，在井下空间布设4个基站，定义为B={B1，B2，B3，B4}，其中基站Bi的位置坐标为{xi，yi，zi}（i=1，2，3，4）且每个基站具有相同的感知半径r和通信半径R。

已知基站Bi的感知范围是一个以{xi，yi，zi}为中心，以 r 为半径的封闭圆形区域。为了简化计算，将该区域离散化为m×n个像素点，定义Dj={x1，y2，z3}（j=1，2，…，m×n），其位置坐标即基站布设优化位置目标，如公式（18）所示。

（18）

式中：d（Bi，Dj）为像素点位置Dj与任一基站Bi之间的欧氏距离，如果存在d ≤ r，则定义该像素点已被信号覆盖。

采用布尔测量模型作为基站感知模型[5]，定义像素点Dj被Bi感知的概率p（Bi，Dj），如公式（19）所示。

（19）

在该区域内，任意一个像素点Dj能够同时被多个基站Bi感知，则定义Dj的联合感知概率p（B，Dj），如公式（20）所示。

（20）

已知区域UWB基站布设区域覆盖率即传感器节点集合B所覆盖的像素点数与区域内所有像素点总数的比值，其定义如公式（21）所示。

（21）

因此，将NOA应用于UWB基站布设优化的目标函数为公式（21），并求解区域覆盖率pcov最大值。

设置NOA相关参数如下，种群规模为30；最大迭代次数为100次；自变量维数为12；δ为0.05；Prp为0.2；Pa2为0.4。

3.3 仿真结果分析

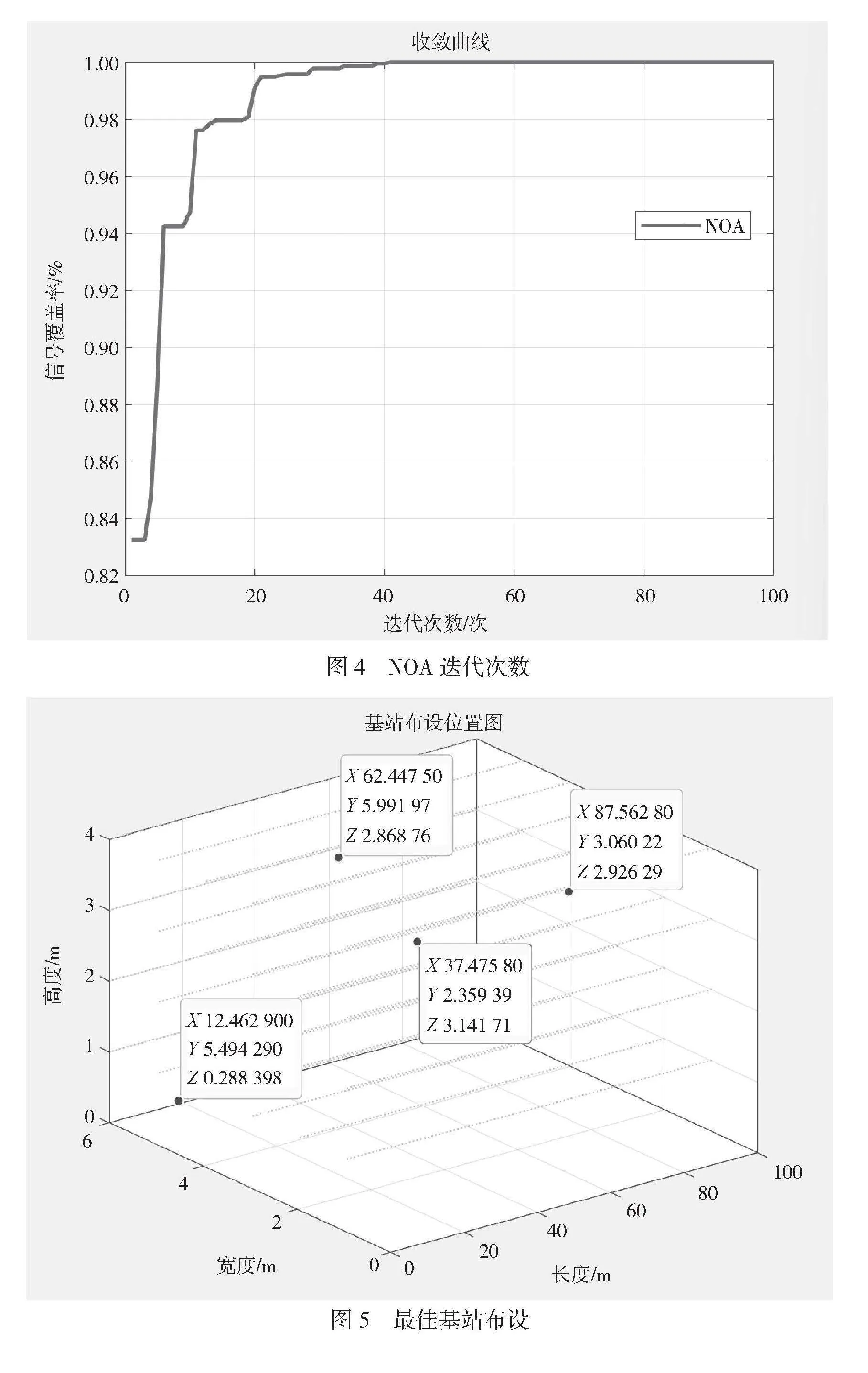
通过NOA模拟仿真，经过Matlab仿真的迭代次数如图4所示，经过100次迭代后，在约束条件内得到最佳基站布设位置，如图5所示。在此布设下，保证基站信号有效覆盖整个目标区域。

4 结语

本研究成功地应用了NOA于UWB定位系统的基站布设优化。通过仿真试验，本文展示了NOA在提高定位精度和覆盖范围方面的显著效果。使用NOA对基站布设进行优化，不仅提高了定位系统的整体性能，而且采用了高效的搜索策略，减少了计算时间和资源消耗。未来研究方向包括利用NOA合理配置基站以最小化位置精度稀释因子，保证覆盖整个目标区域，在井下真实环境中进行测试，进一步优化并改进算法。

参考文献

[1]张岩松.基于UWB 技术的煤矿井下人员精确定位系统研究[D].徐州：中国矿业大学，2021.

[2]杨谊.基于多传感器融合的室内外无缝定位技术研究[D].重庆：重庆邮电大学，2022.

[3]ABDEL-BASSET M，MOHAMED R，JAMEEL M，et al.

Nutcracker optimizer： A novel nature-inspired metaheuristic algorithm

for global optimization and engineering design problems[J].Knowledge-Based Systems，2023（262）：110248.

[4]杨帆.超宽带室内定位系统基站选择方法的研究[D].桂林：桂林电子科技大学，2023.

[5]何庆，徐钦帅，魏康园.基于改进正弦余弦算法的无线传感器节点部署优化[J].计算机应用，2019，39（7）：2035-2043.