基于动态五邻域搜索的改进Astar算法路径规划研究

摘 要：针对传统Astar算法在复杂场景下的路径规划任务中存在路径搜索效率低、路径转折次数多等问题，本文提出一种基于动态五邻域搜索的改进Astar算法。通过改进算法的启发函数，将曼哈顿距离与欧式距离融合得到的距离度量代替传统Astar算法的单一距离度量，引入动态加权机制，并将传统的固定八邻域搜索策略改进为动态五邻域搜索策略。通过剔除最终路径的冗余节点并进行贝塞尔曲线平滑处理，使最终路径更平滑。试验表明，与传统Astar算法相比，采用本文算法的路径搜索时间减少了约69%，路径拓展节点数减少了约66.35%，路径包括节点数减少了约38.8%，路径寻优能力较好。

关键词：Astar；路径规划；贝塞尔平滑曲线；混合加权；邻域搜索

中图分类号：TP 393" " " " " 文献标志码：A

路径规划是解决移动机器人导航问题的关键技术之一。现阶段路径规划方法主要分为2类，一类是以A*算法（Astar）[1]为主的静态全局路径规划算法[2]，另一类是以动态窗口算法（Dynamic Window Approach）[3]为主的动态局部路径规划算法[4]。

Astar算法能在提升搜索效率的同时能兼顾寻找较优路线，已经成为机器人应用中最普遍的全局路径规划算法[5]。但是Astar算法也有局限性，例如当面对复杂场景时，由于障碍物增多，因此Astar算法会搜索大量非必要节点，导致搜索效率降低。

针对传统Astar算法存在的缺陷，国内学者进行了广泛研究，远子涵等[6]提出一种12方向二十四邻域搜索方式的改进Astar方法，该方法减少了搜索路径的拓展节点，节约了搜索时间，但是其规划路径并非最优路径；孔继利等[7]在传统Astar算法中引入双向搜索机制，减少了对拓展节点的搜索，但是未解决规划路径节点冗余、计算时间过长等问题。针对上述问题，笔者提出一种基于动态五邻域搜索的改进Astar算法。该方法通过在启发函数中融入混合距离度量和动态加权机制提高了节点的搜索效率，解决了在搜索过程中内存消耗的问题，并对最终路径进行平滑处理，使机器人行驶轨迹更平滑。

1 传统Astar算法

1.1 Astar算法原理

Astar算法利用启发式函数来估计从当前节点到目标节点的代价，从而引导搜索方向，减少搜索空间，提高搜索效率[8]。Astar算法结合了最佳优先搜索和Dijkstra算法的特点，当寻找起始节点至目标节点的路径时，效率很高，应用价值广泛。

用Astar算法的节点定义评估函数f（n），如公式（1）所示。

f（n）=g（n）+h（n） " " " "（1）

式中：g（n）为从起始节点到当前节点的实际距离；h（n）为当前节点到目标节点的启发式估计距离[9]。

Astar算法的关键是设计启发式函数h（n）。在理想情况下，h（n）应该精确反映从节点n到目标的成本。然而，在实际应用中，Astar算法通常使用欧式距离、曼哈顿距离和切比雪夫距离来近似表示h（n）。

1.2 Astar算法与WAstar算法比较

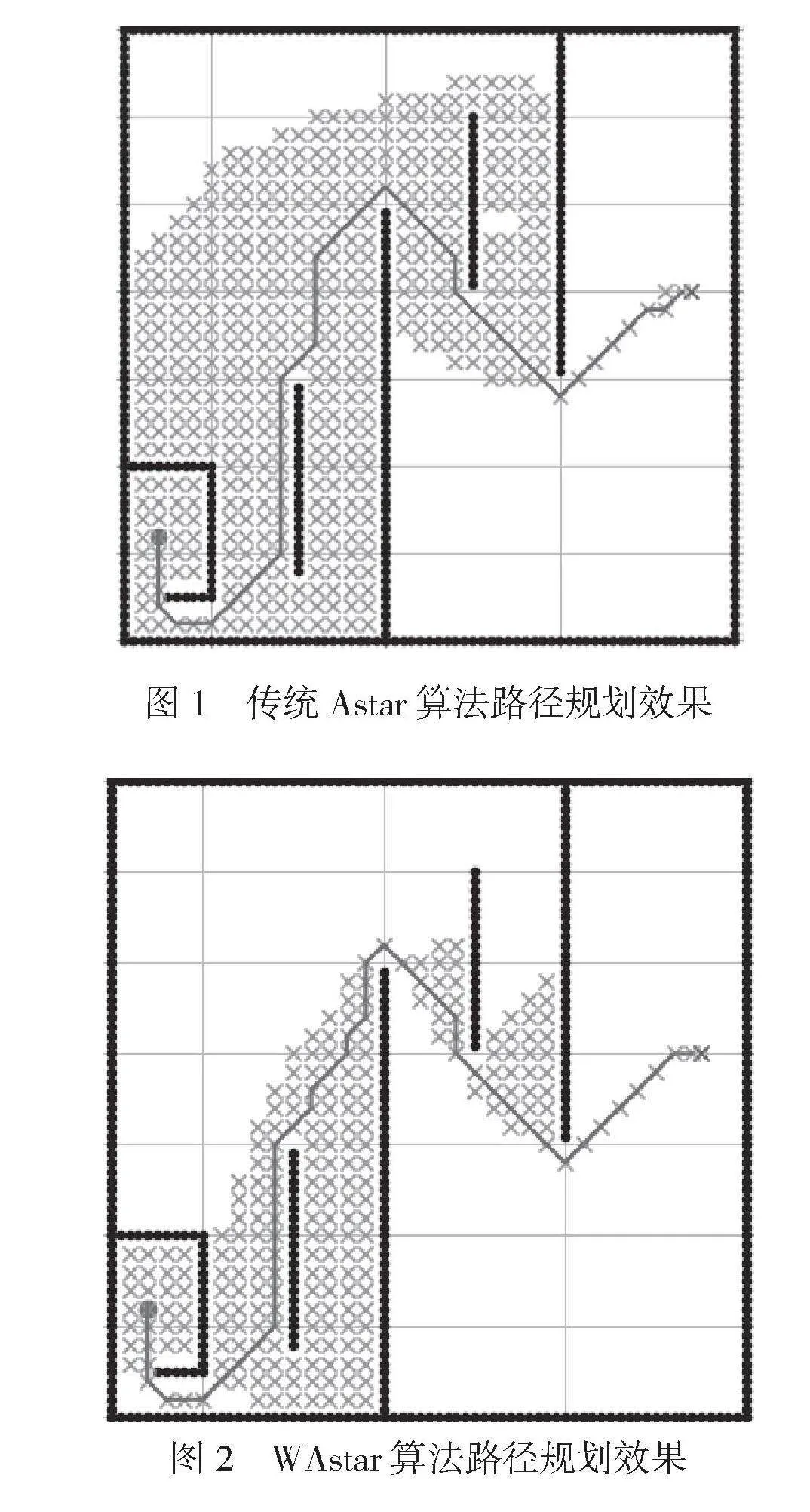
Astar算法基于启发式搜索的思想，估计从起始状态到目标状态的代价，并结合搜索路径中已知的信息来指导搜索过程，以找到最优路径或者满足特定条件的路径。传统Astar算法路径规划效果如图1所示。WAstar算法是在Astar算法的基础上添加启发函数的权重因子，以路径最优性换取搜索速度，WAstar算法路径规划效果如图2所示。

在图1和图2中，深色圆点为起点，深色叉号为终点，浅色叉号为搜索节点。从图2可以看出，与传统Astar算法相比，WAstar算法的搜索节点数量明显减少，搜索速度更快，但是规划的路径并不是最佳路径。

2 改进Astar算法

2.1 混合动态加权

Astar算法的效率和准确性深受其启发式函数h（n）的影响。尽管WAstar算法对h（n）进行了加权处理，与传统的Astar算法相比，搜索效率有了很大程度提升，但是WAstar算法存在一定缺陷，例如无法根据当前结点位置动态选择合适的权重，在WAstar算法中的单一距离度量有一定局限性。

基于上述问题，本文在改进的Astar算法的启发函数中，引入动态加权机制，如公式（2）所示。

f（n）=（1-α）·g（n）+α·h（n） （2）

式中：α为动态加权因子，α随当前点的变化而改变，如公式（3）所示。

（3）

式中：Lstart_goal为起始点到目标节点的欧氏距离；h1（n）为当前点到目标点的欧式距离。该方法使启发函数能够根据实际搜索情况动态调整权重。这种动态加权策略可以更好地平衡搜索的广度和深度，从而提高搜索效率。针对传统Astar算法中单一距离度量的局限性，笔者融合曼哈顿距离与欧式距离，作为新的启发函数距离度量hEM（n），如公式（4）所示。

（4）

式中：h2（n）为当前点到目标点的曼哈顿距离；h3（n）为起始点到目标点的曼哈顿距离；ω为可变倍数。

曼哈顿距离和欧式距离各有特点，曼哈顿距离更适合网格状地图的路径搜索，欧式距离更适合连续空间的路径规划。融合这2种距离度量方式，新的启发函数能够更全面地考虑路径的特性和环境的几何信息，生成更优质的路径。改进后的Astar算法评估函数如公式（5）所示。

f（n）=（1-α）·g（n）+α·hEM（n） （5）

2.2 动态五邻域搜索

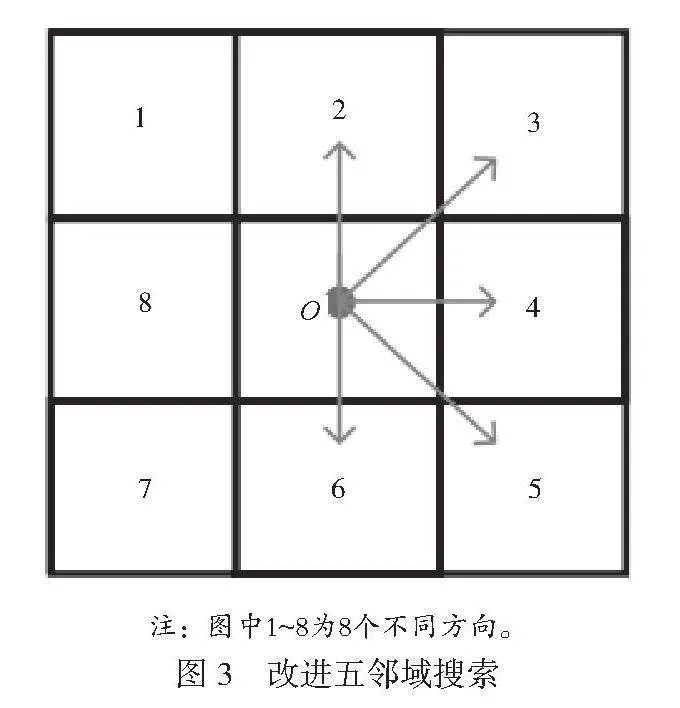
在Astar算法中，传统的八邻域搜索是在二维平面上的节点周围考虑8个可能的移动方向。如果缩小这个范围，只考虑以目标点为导向的5个方向（如图3所示），则可以进一步减轻算法运算负担，从而提高Astar算法的整体运行效率。

仅考虑以目标点为导向进行单一五邻域搜索，当5个邻域方向均存在障碍物时，Astar算法会在该区域陷入死锁状态，无法有效规划路径。为避免发生以上情况，引入动态五邻域搜索理念，在搜索过程中，实时判断当前节点与目标点之间的相对位置关系，方向搜索规则见表1。再根据表1进行动态调整，避免Astar算法陷入死锁状态，更集中地搜索可能包括最优路径的节点，从而提高搜索效率。

表1 方向搜索规则

当前点与目标节点相对位置 保留搜索方向 舍弃搜索方向

第一象限 O2，O3，O4，O5，O6 O1，O7，O8

第二象限 O4，O5，O6，O7，O8 O1，O2，O3

第三象限 O6，O7，O8，O1，O2 O3，O4，O5

第四象限 O8，O1，O2，O3，O4 O5，O6，O7

2.3 路径平滑处理

传统的Astar算法规划的最终路径存在节点冗余、转折点过多等问题，导致移动机器人当沿该路径导航时需要频繁转弯。因此，本文从最终路径起始点开始删除当前节点与前一节点同向运动的节点，进而去除冗余节点。分段处理最终路径，每4个节点1组进行三阶贝塞尔曲线平滑处理，处理规则见表2。如果节点数﹤4个，则根据表2进行贝塞尔曲线平滑处理，从而提高规划路径的可行性。

表2 分段贝塞尔曲线平滑处理规则

分段节点数 贝塞尔曲线策略

4 三阶贝塞尔曲线

3 二阶贝塞尔曲线

lt;3 一阶贝塞尔曲线

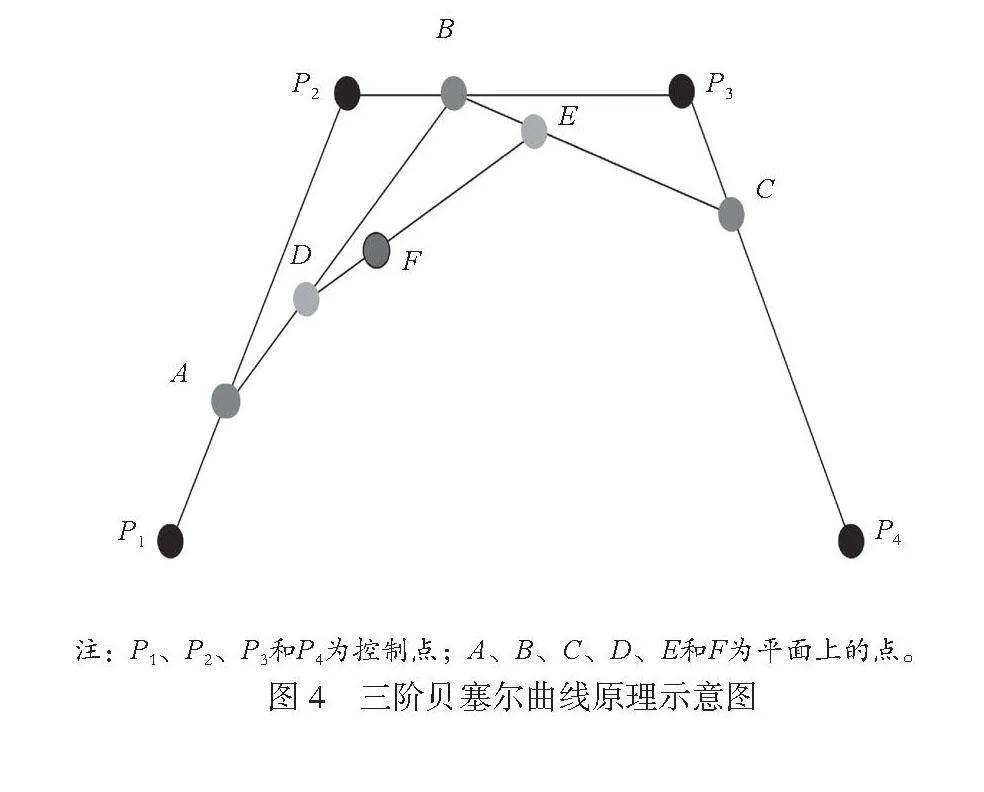
三阶贝尔塞尔曲线原理如图4所示，选取平面内任意4个节点P1、P2、P3和P4作为控制点，在线段P1、P2上选取点A，在线段P2、P3上选取点B，在线段P3、P4上选取点C，如公式（6）所示。

（6）

连接线段AB与线段BC，在线段AB上选取点D，在线段BC上选取点E，如公式（7）所示。

（7）

连接DE，在DE上选取点F，如公式（8）所示。

（8）

将所有满足上述条件的点F相连接，生成的线段就是三阶贝塞尔曲线平滑处理后产生的路径。

3 仿真验证及结果

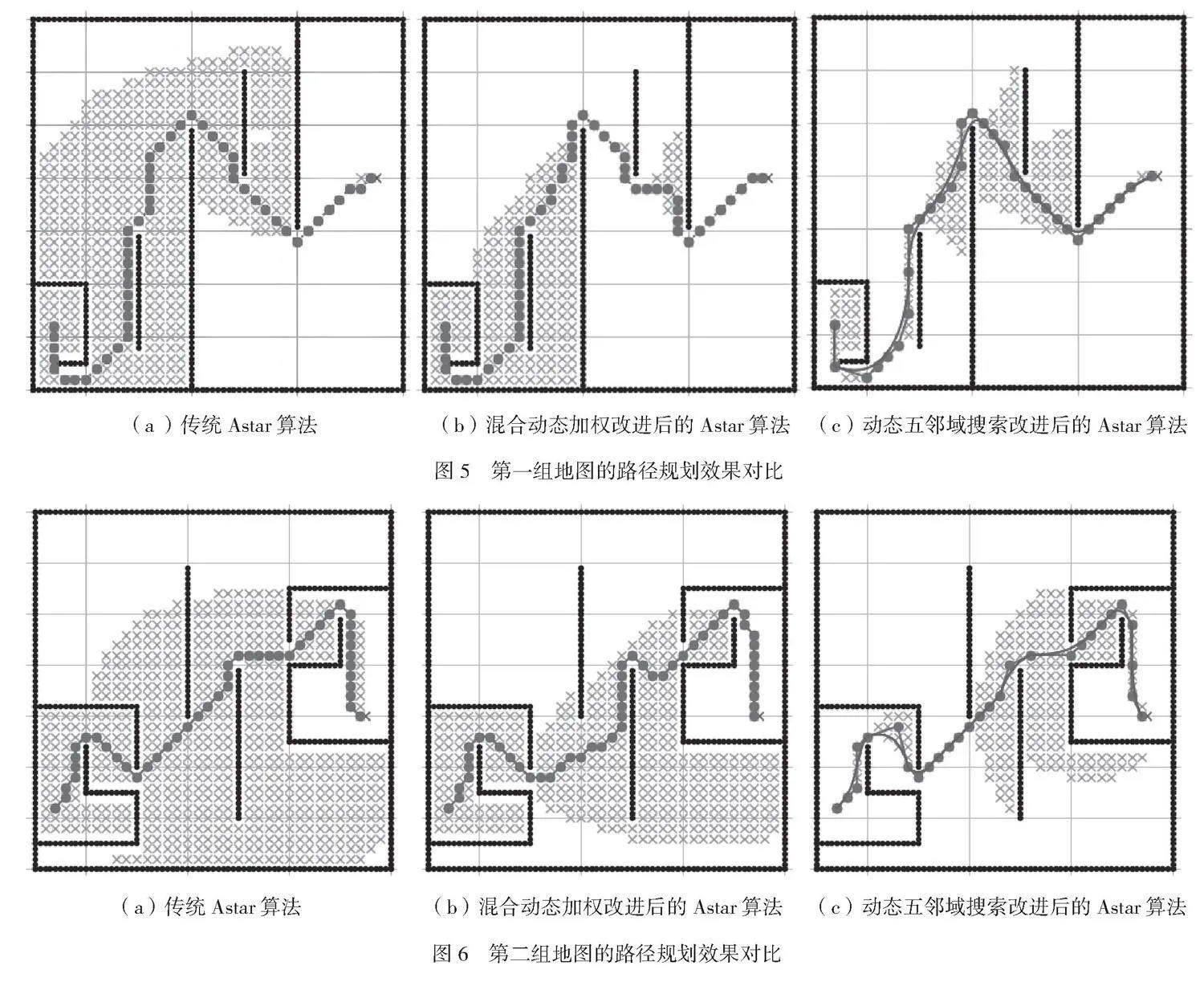
为了提高 Astar算法的有效性，本文基于PC实验平台、Intel Core i7-7500U CPU、GPU NVIDIA GeForce 940MX和12 RAM，分别对传统Astar算法、混合动态加权后的Astar算法和基于动态五邻域搜索的改进Astar算法进行2组不同地图下的仿真试验，以避免由于改进后的算法更适用于某单一场景，因此导致试验结果出现偶然性的情况。2组不同地图的路径规划效果如图5、图6所示。同时对比3种算法在2组不同场景的路径长度、搜索时间、路径拓展节点数和路径

包括节点数，对比结果见表3、表4。

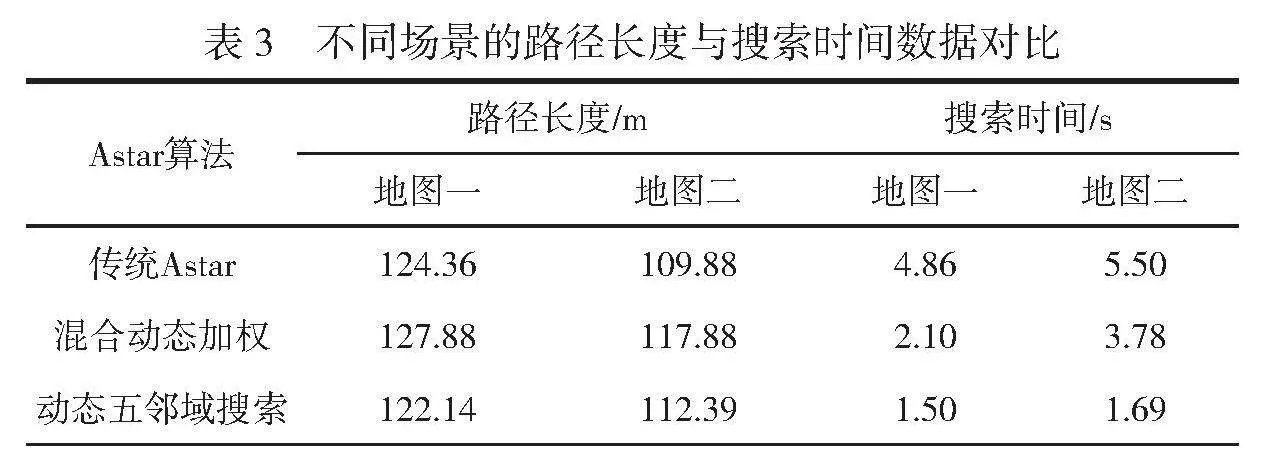
表3 不同场景的路径长度与搜索时间数据对比

Astar算法 路径长度/m 搜索时间/s

地图一 地图二 地图一 地图二

传统Astar 124.36 109.88 4.86 5.50

混合动态加权 127.88 117.88 2.10 3.78

动态五邻域搜索 122.14 112.39 1.50 1.69

由表3可知，使用混合动态加权改进传统Astar算法的启发函数后，与传统Astar算法相比，混合动态加权算法的搜索时间平均缩短了44%，在混合动态加权的基础上引入动态五邻域搜索的改进Astar算法，与传统Astar算法相比，搜索时间平均缩短了约69%。在路径长度方面，当面对场景较为简单的地图时，基于动态五邻域搜索的改进Astar算法路径长度优于传统Astar算法。

表4 不同场景的路径拓展节点数与路径包括节点数数据对比

Astar算法 路径拓展节点数/个 路径包括节点数/个

地图一 地图二 地图一 地图二

传统Astar 505 620 52 46

混合动态加权 238 424 55 50

动态五邻域搜索 164 216 32 28

由表4可知，使用混合动态加权改进传统Astar算法的启发函数后，与传统Astar算法相比，其搜索效率有显著提升，路径拓展节点数平均减少了42.24%。在混合动态加权的基础上引入动态五邻域搜索的改进Astar算法进一步提升了算法的搜索效率，与传统Astar算法相比，路径拓展节点数平均减少了约66.35%。经过冗余节点剔除处理与贝塞尔平滑处理后，规划路径转折点更少，平滑度更高，与传统Astar算法相比，路径包括节点数减少了38.8%。

4 结论

为提高Astar算法的搜索效率，本文提出在传统Astar算法的基础上优化其启发函数，设置动态权重因子α，并将欧氏距离启发函数替换为融合曼哈顿距离与欧氏距离优势的混合启发函数hEM（n），缩短了寻优时间，提高了搜索效率。

将传统Astar算法中八邻域搜索改为动态五邻域搜索，算法目标导向性增强，也避免了在定向五邻域搜索中出现在复杂情况下找不到最优路径的问题。

针对传统Astar算法规划的路径节点冗余、转折点过多和平滑度差等现象，对改进后的Astar算法进行三阶贝塞尔曲线平滑处理，并剔除最终路径冗余节点，减少了转折点个数，提高了路径质量。

参考文献

[1]DECHTER R，PEARL J.Generalized best-first search strategies and the optimality of A*[J].Journal of the ACM，1985，32（3）：505-536.

[2]ZAID T，QURESHI A H，YASAR A，et al.Potentially guided

bidirectionalized RRT* for fast optimal path planning in cluttered

environments[J].Robotics and Autonomous Systems， 2018（108）：13-27.

[3]朱茂飞，胡方亚，李娜可，等.无人驾驶汽车路径规划算法综述[J].农业装备与车辆工程，2023，61（11）：18-22.

[4]李晓旭，马兴录，王先鹏.移动机器人路径规划算法综述[J].计算机测量与控制，2022，30（7）：9-19.

[5]李晨辉，王泽峰，胡德燕，等.移动机器人的路径规划技术研究[J].机电工程技术，2023，52（1）：5-9.

[6]远子涵，张皓，左晋，等.基于12方向24邻域的A*算法路径规划研究[J].北京印刷学院学报，2023，31（9）：38-43.

[7]孔继利，张鹏坤，刘晓平.双向搜索机制的改进A*算法研究[J].计算机工程与应用，2021，57（8）：231-237.

[8]刘梦杰，朱希安，王占刚，等.基于双向A*算法的矿井水灾逃生路径应用研究[J].煤炭工程，2019，51（9）：42-47.

[9]胡杰，朱琪，陈锐鹏，等.引入必经点约束的智能汽车全局路径规划[J].汽车工程，2023，45（3）：350-360.