面积边长固定的四边形对角线长算法及应用

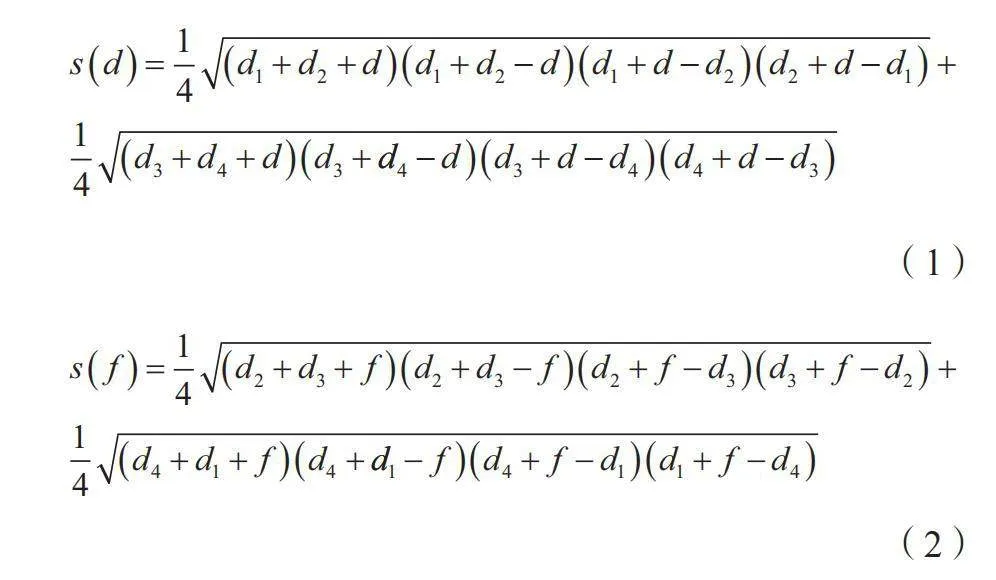
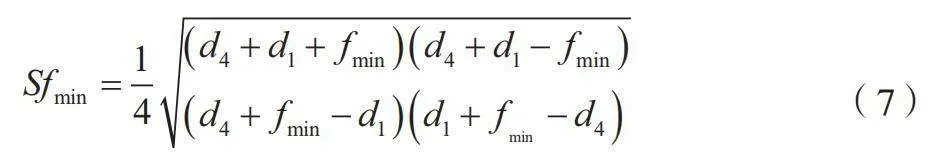
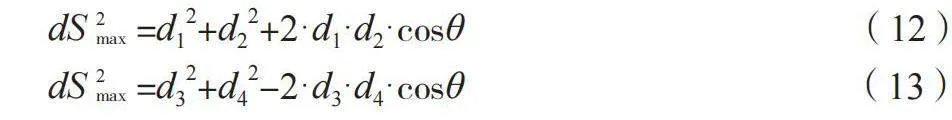
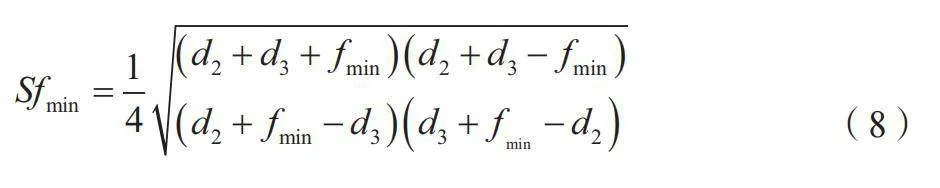
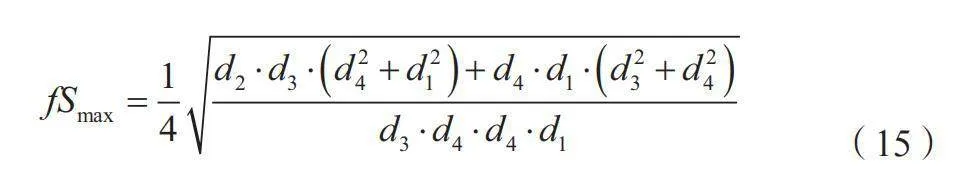
摘 要：不动产宗地界址的恢复可简化为根据四边形的面积和边长确定其对角线长度的问题。本文通过研究四边形对角线长与面积间的关系，建立了求解四边形对角线长的算法模型。在四边形四个边长和面积固定的约束条件下，经迭代计算求解对角线长度。根据已知界址点的坐标用距离交会法计算四边形的两个待定点坐标，从而恢复宗地界址。

关键词：宗地界址恢复；四边形对角线长与面积关系；弦截迭代公式；距离交会

中图分类号：P 20" 文献标志码：A

许多老旧的宗地图受当时测绘技术条件的限制，只有边长和面积，没有坐标，也没有可参照的地形地物。在新的不动产登记调查作业中，要恢复其形状和界址点坐标的同时，还要保证面积边长不变，手工调整难度很大。

任何形状的宗地在大致确定各界址点位置后，均可将该宗地证载面积减去其他不可调整的固定部分面积后的剩余面积，归算到一个四边形上。在保证四边形四个边长一定，面积等于宗地剩余面积的约束条件下，通过迭代计算四边形对角线长，从而将不稳定的四边形变为两个共边的稳定三角形，这样就稳定了该四边形的形状。根据四边形与宗地其他部分的两个衔接点坐标，按照距离交会法可以计算其他两个顶点的坐标，从而恢复老宗地图的界址点。

1 四边形对角线长与面积关系

四边形是一个不稳定的图形，边长一定的四边形其面积是无法固定的。固定四边形的一条对角线后，四边形就成了两个共边的稳定三角形，四边形也变得稳定且具有唯一的固定的面积。

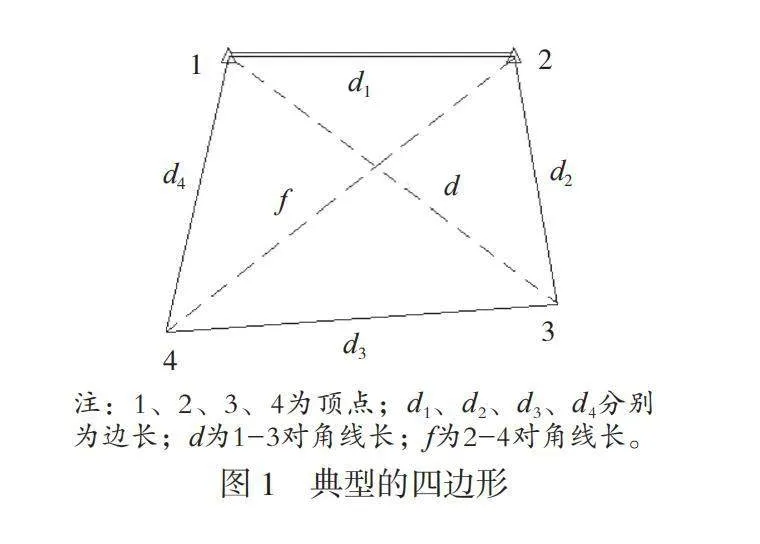
图1为典型四边形，根据海伦公式可以求出三角形123和三角形134的面积，这两个三角形的面积之和便是该四边形的面积，于是便得出四边形的面积S与对角线长度d的函数关系，如公式（1）和公式（2）所示。

（1）

（2）

2 求解角线长度

当四边形的面积一定时，公式（1）或公式（2）可求出对角线长度d或f。由于公式（1）和公式（2）不是线性方程，因此无法直接求解，须采用迭代法进行计算。

2.1 对角线长度的取值范围及面积极值

在图1中，设1、2顶点是固定的已知点，3、4顶点为待定点。当压缩或拉伸对角线d时，面积S也将随之变小或变大。

2.1.1 对角线长度的最小值

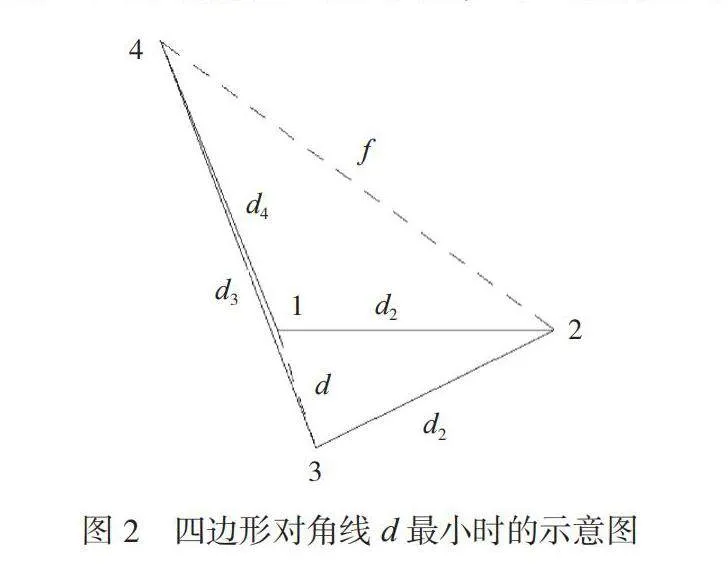
在图1的基础上，使顶点3向顶点1靠近，不断缩短d。受4个固定边长的约束，凸四边形将会压缩为凹四边形，面积逐渐变小，较短的边会向里折叠，最终有2条边折叠在一条直线上，此时的图形为一个小三角形加一段回头线，d压缩至最小（图2）。

d的最小值dmin如公式（3）所示。

dmin=max（|d1-d2|，|d3-d4|）" " " " " " " " " " " " "（3）

式中：max（）为取最大值函数。

根据海伦公式，可求出d最小时的面积，当dmin=|d1-d2|时，如公式（4）所示。

（4）

当dmin=|d3-d4|时，如公式（5）所示。

（5）

同理，计算f的最小值如公式（6）所示。

fmin=max（|d2-d3|，|d4-d1|）" " （6）

当fmin=|d2-d3|时，计算四边形面积如公式（7）所示。

（7）

当fmin=|d4-d1|时，计算四边形面积如公式（8）所示。

（8）

注意图2，这个时候的f已经跑到了四边形的外面，因此这时的f变得没有意义，就不能再用f去求解四边形了。对角线d或f必须在四边形内部，当d或f跑到四边形外面时，使得公式（1）或公式（2）不成立。

在d达到图2所示的最小值后，若将f变小，则会使d也跑到四边形的外面，而且这时的四边形就会自相交，这在图形的拓扑关系中也是不允许存在的。因此，在后续的研究中，本文仅考虑d或f在四边形内部时的情形。

2.1.2 对角线长度的最大值

在图1的基础上，将顶点3向外拉伸，使其与顶点1的距离增加，d不断变大。受4个固定边长的约束，图形将会逐渐撑开变为凸四边形，在该过程中，面积逐渐变大。当变化到4个顶点共圆时，四边形的面积达到最大极值。此时继续拉伸d，四边形将会变得瘦长，最终2条较短的边被拉伸为一条直线，图形变为一个大三角形，d拉伸最大（图3）。

此时得到公式（9）。

dmax=min（d1+d2，d3+d4）" " " " " " " " " "（9）

式中：min（）为取最小值函数。

同理，计算f的最大值如公式（10）所示。

fmax=min（d2+d3，d4+d1）" " " " " " " （10）

2.1.3 四边形面积的最大值

已有研究表明，当四边形的4个顶点共圆时面积最大[1]，最大面积如公式（11）所示。

（11）

如上所述，四边形面积最大时四个顶点共圆，即为圆内接四边形。根据圆内接四边形对角互补的性质可知，图1中的∠123与∠341之和为π。设∠123为θ，则∠341为π-θ。设面积最大时1-3对角线长度为dSmax，根据余弦定理并顾及cos（π-θ）=-cosθ，得出公式（12）和公式（13）。

dS2 max=d12+d22+2·d1·d2·cosθ " " " " " " " " " " " " " " " " （12）

dS2 max=d32+d42-2·d3·d4·cosθ " " " " " " " " " " " " " " " "（13）

解上述方程组可得公式（14）。

（14）

同理可得，计算面积最大时2-4对角线的长度如公式（15）所示。

（15）

2.2 构建迭代模型

2.2.1 S（d）与S（f）函数曲线的特性分析

由上文可知，当d或f在四边形内部时，将其作为2个三角形的共边，以此计算四边形的面积才是有意义的。在观察对角线d变化过程中发现，d与f是联动的关系。在d和f均在四边形内部的区间内，d变大f必然变小。反之，f变大d就变小。在该区间内，d与f是互替的关系，即求解d与求解f可以得到相同的四边形。

当d拉伸至最大（大三角形）时，f还有继续变小的可能。当d为最大值时（如图3所示），顶点2继续向顶点4靠近，图形将变形为凹四边形。f继续变小，图形最终会稳定在一个带回头线的小三角形上。此时d已经在四边形外且开始变小。在该区间内，d失去其意义，根据f来确定四边形的形状。反之，当f拉伸至最大，d仍继续变小时，f也失去意义，须根据d来确定四边形。这两个区间是d与f的互补区间。典型的四边形对角线长度与面积关系曲线如图4所示（为清楚地说明d和f两个对角线的联动关系，将f轴的方向指向了与d相反的左边）。

结合图4，总结四边形的S（d）曲线和S（f）曲线特性，得出以下结论。1）随着对角线长度的值由小变大，四边形面积会经历一个由小变大、达到极值后再由大到小的过程。在上升区间或下降区间内S（d）和S（f）都具有单值属性，因此在各自的上升区间或下降区间内，给定S就可以迭代出d或f。2）S（d）的下降段（粗虚线部分）与S（f）对应的上升段（细实线部分）是完全等效的，同一个面积值，二者计算的四边形完全一样。反之，S（f）的下降段（细虚线部分）与S（d）上升段（粗实线部分）对应部分也是这样。在上述区间内，当面积一定时求解d与f可以得到相同的四边形，二者可以互替。3）对比图2与图3，Sdmin≤Sdmax，Sfmin≤sfmax。即图4曲线的上升区间的面积值完全可以涵盖下降区间的面积值。

由上述分析可以看出，将S（d）和S（f）的上升段（各自的实线部分）合并在一起而忽略其下降段（各自的虚线部分），就能得到一个完整的曲线图。当设计程序时，仅考虑S（d）和S（f）的上升段，会使解算模型变得较为简单。另外，由图4可以看出，S（d）和S（f）的下降段比较陡，d或f的误差对S的影响也会较大。因此，仅用S（d）和S（f）上升段的另一个优势可获得较好的精度。

若Sdmin≤S≤Smax，则可以用S（d）函数在dmin≤d≤dSmax区间迭代d的目标值，以此得到四边形的第一组解。若Sfmin≤S≤Smax，则可以用S（f）函数在fmin≤f≤fSmax区间迭代f的目标值，以此得到四边形的第二组解。若S在Sdmin和Sfmin间，则只能有一组解。

2.2.2 迭代公式

当四边形边长和面积确定后，要根据公式（1）和公式（2）分别迭代1-3对角线长度和2-4对角线长度。

假定对角线长度为x，根据公式（1）或公式（2）即可得出四边形面积的计算值S（x）。设四边形的给定面积为S，则面积残差为：v（x）=S（x）-S。根据不动产调查技术规程，面积精度为0.01，因此，将面积残差的容许值ds（面积容差）设定在比其小10倍的0.001。当残差大于容差时，通过增加或减少x值，再次计算残差，直至残差小于或等于容差为止，这样即可迭代出x的目标值d或f。

实际计算时，采用弦截迭代公式，计算过程如公式（16）所示[2]。

（16）

弦截迭代公式需要两个初值：x0和x1，这两个初值均不能超过目标值。v0和v1是根据两个初值计算的面积残差。当迭代d时，x0=dmin，当迭代f时，x0=fmin。x1=x0+dx，其中dx为一微小变化量。

要保证dx引起的面积变化量小于容差。以迭代d为例，由图1和图3可以看出，当f最大时，d的变化对面积的影响最大，可表示为ds=dx·fmax，因此取dx=ds/fmax。同理，当迭代f时，dx=ds/dmax。由于设定面积容差值时已经留有充分冗余，因此求出的初值不会超过目标值。

2.2.3 迭代过程

以迭代对角线d为例。

确定两个初值：x0=dmin、x1=x0+dx，其中dx=ds/fmax，ds=0.001。

计算初值的四边形面积残差：将d=x0、d=x1 代入式（1），计算d取两个初值时的四边形面积S（x0）、S（x1），然后按照残差公式v（x）=S（x）-S计算四边形面积的两个残差：v0=v（x0）、v1=v（x1）。

将两个初值x0、x1和两个残差v0、v1代入公式（14）计算第一次迭代值x，并按残差公式计算四边形面积残差v。

若vlt;ds或xgt;=dSmax则结束迭代，取d=x；否则x0=x1，v0=v（x0），x1=x，v1=v（x1）重复公式（2）～公式（4）。

3 计算顶点坐标

计算对角线d和f后，根据顶点1和2的坐标，用距离交会法可求出顶点3和4的坐标。距离交会法可以计算两个相交圆的交点坐标。以交会顶点3（x，y）为例，已知点1（x1，y1）和点2（x2，y2）到顶点3的距离分别为r1和r2，通过求解两个圆的联立方程即可得到交点坐标（x，y），如公式（17）所示。

（17）

式中：；

r2=（x2-x1）2+（y2-y1）2。

需要说明的是，两个相交圆将会有两个交点，其中一个交点与圆心构成的三角形1-2-3为顺时针，另一个则为逆时针。宗地图中的界址点是按顺时针进行编号的，因为当对图1所示的四边形的顶点和边长进行编号时也是采用的顺时针，所以公式（17）所取的是顺时针的那个解（将b反符号后是逆时针的那个解）。

4 计算机程序实现过程

计算机程序实现过程有以下步骤。1）拾取已定的1、2点坐标，同时反算边长d1，录入面积和其他3个边长。2）根据四边形“任意三边之和大于第四边”，检查录入的边长数据的合理性。若不合理，则终止。3）计算dmin、Sdmin、fmin、Sfmin、Smax、dSmax、fSmax、dmax、fmax，同时求出面积的最小值：Smin=min（Sdmin，Sfmin）。4）根据面积的上下限，检查录入面积数据的合理性。若不合理，则终止。5）迭代计算求出d和（或）f。6）根据距离交会法计算待定顶点坐标。7）在CAD中展绘计算结果。

当解算结果有两组时，须人工判别最合适的结果。

5 结语

宗地界址恢复作业时，首先将能够确定的宗地界址绘制在CAD图上，其次将剩余面积归算到一个待定的四边形上，借助计算 边长和宗地剩余面积确定待定的两个顶点，最后恢复所有宗地界址点。

参考文献

[1]王兵权.论边长确定的四边形面积最大值定理[J].中学教研（数学），2010（9）：25-26.

[2]喻文建.数值分析与算法[M].2版.北京：清华大学出版社，2015.