考虑动态拥堵的城市配送绿色车辆路径问题研究

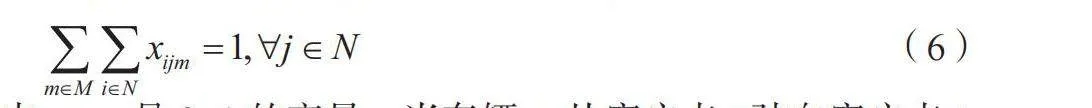
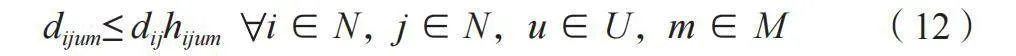
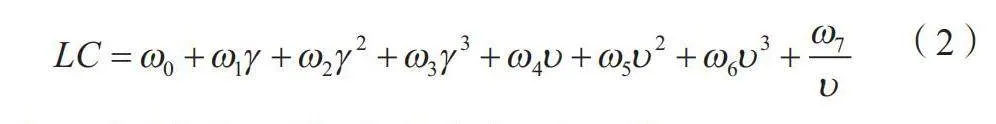
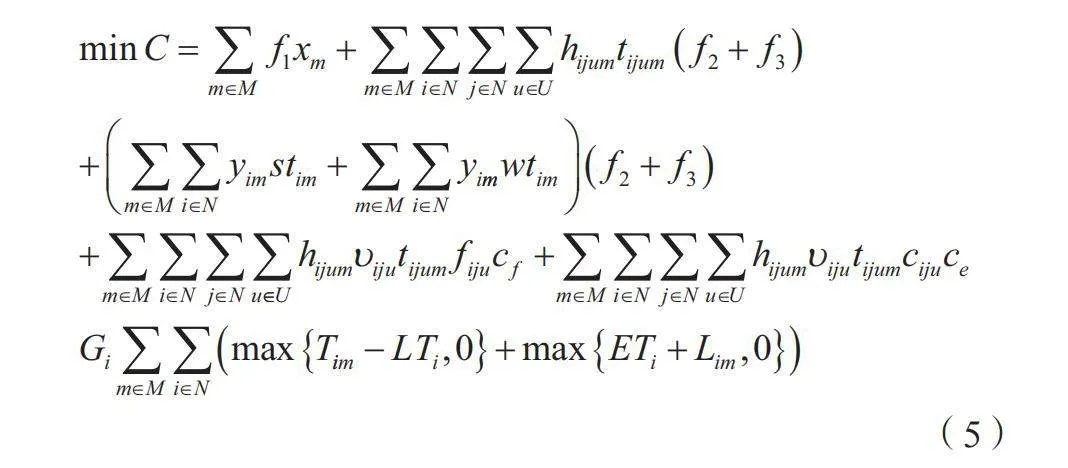
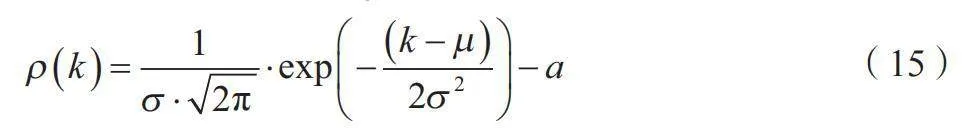
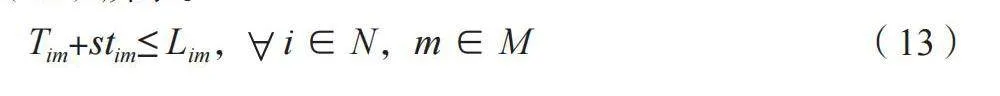
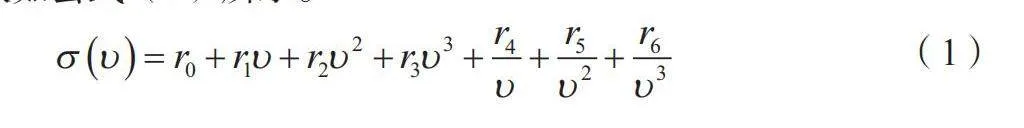
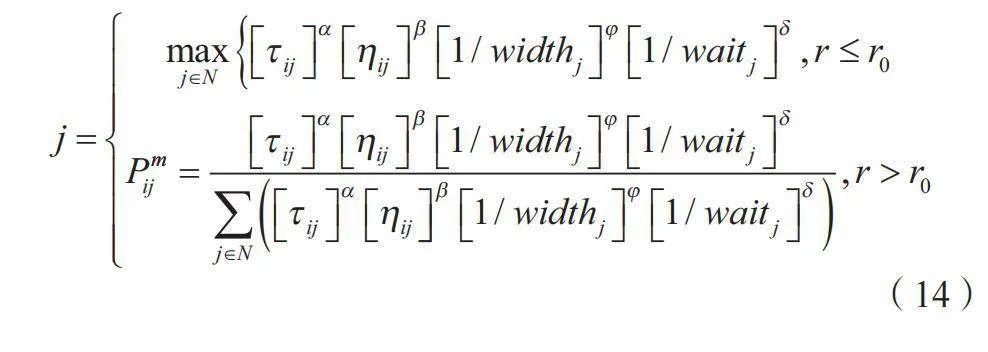
摘 要：针对目前研究城市配送车辆路径多未考虑交通动态拥堵对运营成本的影响，本文将道路拥堵因素引入绿色车辆路径问题（GVRP）的优化数学模型中，以不同的拥堵速度来反应各时间段的交通状况，并考虑碳排放和客户时间窗的影响，建立了以总成本最小化为目标的优化模型，设计了蚁群-遗传混合算法（ACO-GA）进行求解。并结合案例进行分析，将所得结果与蚁群算法（ACO）、遗传算法（GA）进行比较，验证了模型和算法的可行性和有效性，降低了总成本和碳排放，为企业节约成本和绿色转型提供了有力支持。

关键字：绿色车辆路径问题；动态拥堵；碳排放；蚁群-遗传混合算法

中图分类号：TP 30" " " " " 文献标志码：A

随着城市化进程加速，城市交通状况越来越复杂，环境污染问题也越来越严重。因此，城市配送绿色车辆路径问题是目前绿色物流的重要研究领域[1]。在城市配送环节中，车辆的合理使用和规划可以有效提高交通运输效率、缩短配送时间并降低物流成本，同时也能降低对环境的负面影响，保护生态环境，提高城市居民的生活质量。将绿色交通理念和城市可持续发展理念相结合，不仅可以推动城市绿色发展，还可以提高城市的品牌形象和吸引力[2]。

本文关注城市交通动态拥堵的GVRP，即一个配送中心为多个客户点进行配送。考虑不同时间段的车辆行驶速度受交通状况影响，找到最佳的车辆调度和路径规划方案，以达到最小化总成本的目标。为了便于分析，本文做出以下7个假设。1）配送的车辆为同类型车辆且能满足全部需求。2）车辆配送完成后，需要返回配送中心。3）每个客户点的需求量不超过车辆的载重且只能被服务一次。4）已知每个客户点的需求量、位置坐标和时间窗要求等信息。5）车辆的工作运营时间不得超过其最大运输时间。6）车辆为非恒速行驶。7）车辆提早或者迟到到达需要承担相应惩罚。

1 模型构建

1.1 车辆碳排放率和油耗率的计算

不仅行驶距离会影响车辆的碳排放量，车速、车辆载重、交通拥堵和车辆特征等因素也会影响油耗和碳排放。本文使用HICKMAN[3]提出的MEET模型进行计算，碳排放率估计函数如公式（1）所示。

（1）

式中：υ为车辆行驶速度，使碳排放率最小的最优速度υ*为71km/h[4]；r0、r1、r2、r3、r4、r5、r6分别为预定义参数。

载重修正因子LC如公式（2）所示。

（2）

式中：γ为车辆实际载重与额定载重的比值；ω0、ω1、ω2、ω3、ω4、ω5、ω6、ω7分别为预定义参数，其取值受车辆载重的影响。

由此可得车辆的碳排放率ciju（kg/km），如公式（3）所示。

ciju=σ（υ）LC/1000 （3）

本文取1L汽油可以产生2.32kg的碳排放量[5]，计算得出1kg碳排放量对应的油耗量为∂=1/2.32=0.431L/kg，进而得出车辆的油耗率如公式（4）所示。

fiju=∂ciju （4）

1.2 数学模型

根据上述分析，将所有车辆的使用成本、油耗成本、碳排放成本以及时间惩罚成本之和作为优化目标构建GVRP模型，如公式（5）～公式（13）所示。

总成本最小化如公式（5）所示，其中车辆的使用成本包括固定发车成本、行驶时间成本、服务时间成本和等待时间成本。

（5）

式中：N为节点集合，N={i，j|i，j=0，1，1，...，N}；0为配送中心；M代表车辆的编号集合，M={m|m=1，2，...，M}；U为路段划分集合，U={u|u=1，2，...，U}；f1、f2、f3分别为车辆的单位发车成本、单位时间成本和单位人力成本；υiju为车辆在时间段u内在道路（i，j）上的行驶速度；tijum为车辆m在时间段u内以速度υiju在道路（i，j）上行驶的时间；stim为车辆m在节点i的服务时间；wtim为车辆m提前到达节点i的等待时间；cf为单位油耗费用；ce为单位碳排放费用；Gi为惩罚系数；Tim为车辆m到达节点i的时间；[ETi，LTi]为客户点i的服务时间窗；Lim为车辆m离开节点i的时间；xm是0～1的变量，当车辆m使用时为1，否则为0。

每个客户点只能被服务一次，如公式（6）所示。

（6）

式中：xijm是0～1的变量，当车辆m从客户点i驶向客户点j则为1，否则为0。

车辆只能从配送中心出发，并在工作完成后返回配送中心，如公式（7）所示。

（7）

如果客户点i由车辆m服务，则为1，否则为0，如公式（8）所示。

（8）

式中：yim是0～1的变量。

车辆的m实际载质量不得超过该车辆的负载能力，如公式（9）所示。

（9）

式中：qi为客户点i的需求量；Q为配送车辆的容量。

车辆使用数量不能超过配送中心车辆可用数量，如公式（10）所示。

（10）

各车辆的运行工作时间不得高于其最大运输时间，如公式（11）所示。

（11）

式中：tij为从节点i到节点j的运输时间；Tm为车辆m的最大运输时间。

dijum和dij间的限制关系如公式（12）所示。

dijum≤ dijhijum" i∈N，j∈N，u∈U，m∈M （12）

式中：dijum代表车辆m在时间段u内在道路（i，j）上的行驶距离；dij代表从节点i到节点j的距离；hijum代表0～1的变量，当车辆m在时间段u内从节点i到j时则为1，否则为0。

车辆到达客户的时间、服务时间与离开时间的关系如公式（13）所示。

Tim+stim≤ Lim，i∈N，m∈M （13）

2 算法设计

2.1 对选择下一节点概率的改进

在蚁群算法中，改进选择下一节点的概率对优化搜索效率和结果质量至关重要。这种改进可以增强算法的灵活性，使其更好地适应复杂多变的问题环境。通过调整概率计算方式，算法能够在探索新路径和利用已知最优路径间找到更好的平衡，从而提高找到全局最优解的概率。此外，这种改进还有助于加快算法的收敛速度，减少无效探索，有效提升算法的总体性能和应用价值。本文通过引入顾客点时间窗口间隔因素widthj=LTj-ETj来求解下一节点服务的紧急程度，并将等待时间长度因素waitj=ETj-Tj加入蚁群算法中。因此，蚂蚁从一个点向另一个点的移动遵循公式（14）所示的规则[6]。

（14）

式中：τij和ηij分别为信息素浓度和能见度（ηij=1/dij）；α、β、φ、δ分别为信息素浓度、能见度、时间窗口间隔因素和等待时间长度因素的相对重要性，取值分别为1、2、2、3；r为随机变量，在[0，1]上服从均匀分布，r0（0≤r0≤1）是用来控制转移规则的参数。

2.2 信息素挥发因子ρ的改进

通过对蚁群算法中的信息素挥发因子ρ进行改进，能够进一步提高算法解决问题的能力。调整信息素挥发速度有助于保持算法在全局搜索和局部搜索间的动态平衡，避免算法过早陷入局部最优而忽视了其他潜在的优秀解。这种平衡确保了算法在搜索过程中既能广泛探索解空间，又能有效利用当前已知的最优路径，从而在提高解的质量和搜索效率方面有更好的表现。当ρ过小时，蚁群很容易重新选择以前的路径，从而极易陷入局部最优值；当ρ取较大的数值时，虽然可以提高其整体寻优能力，但是迭代次数也会显著增加，从而影响其收敛速度。在此基础上，本文引入了一种随迭代次数增加呈高斯分布的信息素挥发因子ρ，如公式（15）所示。

（15）

式中：k为迭代次数，服从参数σ、μ的高斯分布；σ、μ、a的值可进行自适应调整，本文σ、μ取值分别为7.6、100。

2.3 路径交叉

针对蚁群算法的迭代问题，本文提出了一种基于遗传算法的改进方法，因此拟采用遗传算法中的染色体交叉作业，对每一次迭代后获得的运动轨迹进行二次优化，以提高解决问题的效率和质量。通过模拟自然选择的机制，遗传算法可以在蚁群算法的基础上进一步探索解空间，提供更多样化的解候选。这种结合能够加快算法的收敛速度，提高找到全局最优解的概率，尤其是在处理复杂多变的优化问题的过程中，能够有效避免陷入局部最优解，增强算法的鲁棒性，具体操作包括以下4点。1）在现有算法的迭代过程中选取当前最好的路线，将所有路线的1/n作为群体的一部分，采用轮盘赌的方式，产生剩余的（n-1）/n个初始群体。2）在初始群体中随机选择2条路线，将其作为亲本进行染色体交叉。3）在此基础上，对亲代路径上所有相同的节点进行随机选择，并对其进行分段交叉作业，得到2条子路径。4）在所有的子路线中寻找最佳路线，如果路线的总费用低于目前路线或者全局路线，就用它来替代目前路线和全局路线。

2.4 算法步骤

本文的改进蚁群算法求解优化模型共包括7个步骤。1）构建车辆运输模型，调试算法参数，设置起点和终点位置。2）蚂蚁从起点出发寻找最优运动路径。3）根据引入的启发式函数的概率公式，得出蚂蚁的下一个移动节点。4）判断每只蚂蚁是否移动到终点，如果到达终点，算法运行下一步，否则返回第3步。5）记录每只蚂蚁的路径长度，选择当前迭代中的最优路径，并更新全局最优路径。6）在当前迭代中，根据遗传算法的染色体交叉操作来选取路径进行交叉重组，用交叉后的路径替换当前最优路径与全局最优路径。7）判断是否达到终止条件，如果是，则输出全局最优解，否则返回第2步。

3 算例仿真

对某配送中心的配送路径进行优化，使用同种类型车辆来进行服务，运输车辆容量为4t，车辆对应的碳排放率的系数r为r0=110、r1=0、r2=0、r3=0.000375、r4=8702、r5=0和r6=0[3]。与其相对应的载重修正因子系数为ω0=1.27、ω1=0.0614、ω2=0、ω3=-0.0011、ω4=-0.00235、ω5=0、ω6=0和ω7=-1.33。其他费用的参数设置为f1=550元/辆、f2=80元/h、f3=30元/h、cf=7.95元/L和ce=0.0528元/kg[4]。配送中心的工作时间是6：00～22：00，总计16h，即960min。本文将早上7：00～9：00、晚上18：00～20：00设置为交通拥挤时段，在这段时间内，车辆会以拥堵速度υc行驶，其他时段以正常车速υf行进，υf和υc分别取值为71km/h和20km/h。客户信息见表1，其中0代表配送中心。

本文在MATLAB R2021a中对程序进行编程和实现，其中蚁群算法的种群数量为50，迭代次数设置为400，、α、β、φ、δ取值分别为1、2、2、3；遗传算法的种群规模为80，迭代次数为400，交叉算子为0.9，变异算子为0.1。

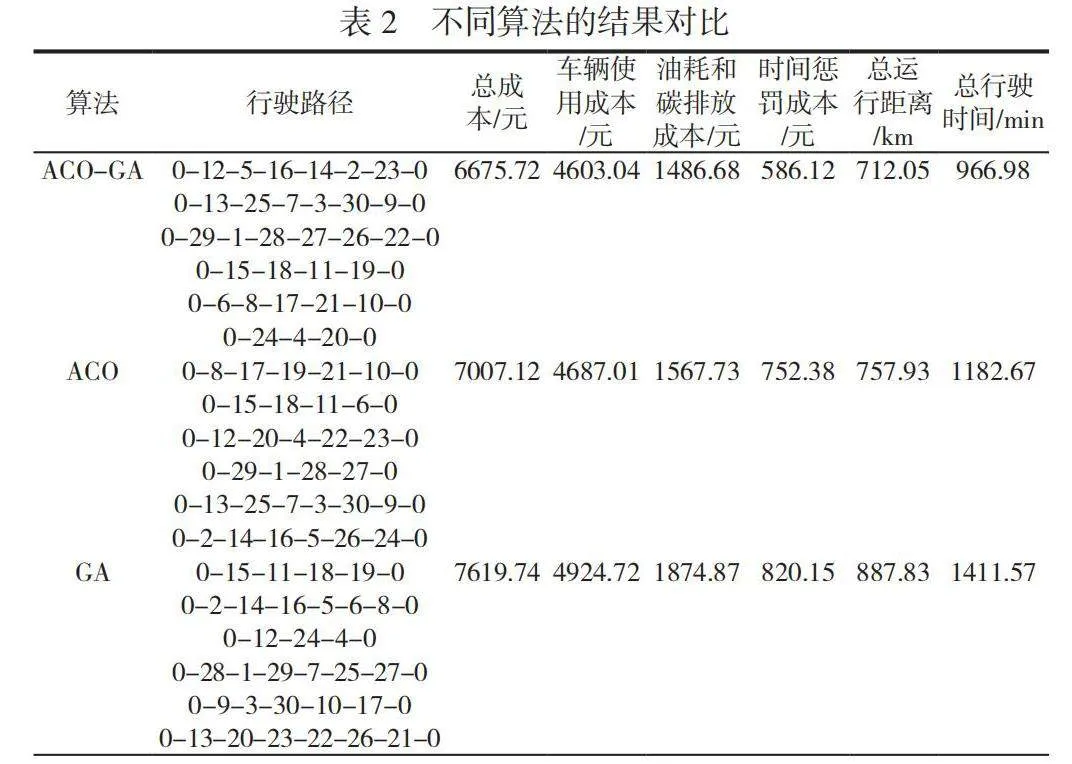
分别采用传统的ACO、GA和改进后的ACO-GA来求解该问题模型，所求结果见表2。

由表2的数据结果可知，在基于ACO算法的求解方法下，车辆最终配送总成本为7007.12元，总运行距离为757.93km，总行驶时间为1182.67min，其中车辆使用成本为4687.01元，油耗和碳排放成本为1567.73元，时间惩罚成本为752.38元。在基于GA算法的求解方法下，车辆最终配送总成本为7619.74元，总运行距离为887.83km，总行驶时间为1411.57min，其中车辆使用成本为4924.72元，油耗和碳排放成本为1874.87元，时间惩罚成本为820.15元。在本文ACO-GA算法的求解方法下，车辆最终配送总成本为6675.72元，比对照组减少了331.28元、943.9元；总运行距离为887.83km，比对照组减少了45.88km、175.78km；总行驶时间为1411.57min，比对照组减少了215.69min、444.59min。其中车辆油耗和碳排放成本为1486.68元，比对照组减少了81.05元、388.19元；时间惩罚成本为586.12元，比对照组减少了166.26元、234.03元。由此可以得出结论，本文算法比对照组具有较好的可行性和有效性，不仅能为企业节约总成本，减少资源浪费，还能有效降低碳排放量，推动城市的绿色发展。另外，时间惩罚成本的降低也表明，用该算法对模型进行求解能使车辆到达客户点更准时，用户体验感更好。

4 结语

随着对环境保护意识的提升，绿色物流在城市配送中越来越重要。在车辆路径规划中提高配送效率、减少配送成本和提升客户体验是城市配送中的重要目标。配送效率的提升需要更快速、更准时的配送，而成本的降低则能提高企业的竞争力。同时，优质的客户体验也能增加客户的忠诚度，促进业务增长。同时，考虑环保因素、降低碳排放并推动城市朝着可持续的方向发展也具有重要的现实意义。因此本文提出了一种考虑动态拥堵的城市配送绿色车辆路径优化模型，并设计了蚁群-遗传混合算法进行求解。研究发现，本文建立的模型和提出的算法可有效降低车辆的配送成本、缩短运输距离并减少行驶时间。同时，车辆油耗和碳排放量也得到了有效降低，这不仅减少了温室气体排放，对环境有益，也为企业的可持续发展奠定了良好基础。

参考文献

[1]张得志，张湘鹏，王润泽，等.基于两阶段的超大型城市物流网络选址与服务路径优化[J].铁道科学与工程学报，2023，20（4）：1270-1279.

[2]王常博.低碳城市视角下我国绿色物流发展研究[J].物流科技，2022，45（18）：24-26.

[3]HICKMAN A J.Methodology for calculating transport emissions and energy consumption[R].European：Cold Starts，1999.

[4]李进，张江华.基于碳排放与速度优化的带时间窗车辆路径问题[J].系统工程理论与实践，2014，34（12）：3063-3072.

[5]TORO E M，FRANCO J F，ECHEVERRI M G，et al.A multi-objective model for the green capacitated location-routing problem"considering environmental impact [J].Computers amp; Industrial engineering，2017（110）：114-125.

[6]吴隽，陈定方，李文锋，等.基于改进蚁群算法的有时间窗车辆路径优化[J].湖北大学学报，2008，23（3）：9-12.