无人机倾斜摄影三维模型自动单体化技术研究

摘 要：基于倾斜摄影的实景三维模型是mesh面，在实际GIS应用过程中，需要对模型进行单体化处理。目前，传统的方法采用DP modeler或者3DMAX等软件进行单体化建模，效率低，成本高。本文研究基于多边形剪裁的实景三维模型单体化技术，采用三角网索引，实时动态的LOD技术和多边形裁剪等技术，在原mesh模型的基础上，提取建筑、道路等地理实体平面位置，根据平面位置将地理实体从mesh网格模型中切割出来，同时对模型侧面进行平滑处理，开发三维模型自动单体化软件。该技术在新疆某大面积实景三维模型项目建设中得到应用，改变了传统单体化建模的手工建模方法，成倍地降低了三维建模单体化和修模生产成本。

关键词：无人机倾斜摄影测量；多边形剪裁；自动纹理映射；LOD技术

中图分类号：V 297" " " " " " " " " 文献标志码：A

倾斜摄影技术是测量测绘领域发展起来的一项高新技术。基于倾斜摄影测量的实景三维中国建设，是数字中国建设的重要组成部分，是国家重大时空基础设施项目。2023年，实景三维中国建设进入全面实施阶段。倾斜摄影自动化建模的技术机制，决定了输出的模型没有对单独的地物进行物理区分，而是一个连续的Tin网。倾斜摄影模型的大多数应用都需要能单独选中建筑等地物，赋予并查询属性等基本GIS功能，单体化问题是倾斜摄影模型在GIS应用中需要解决的重要问题。目前，传统的方法采用DP modeler或者3DMAX等软件进行单体化建模，工作效率低，耗费大量的人力和物力。本文研究基于多边形剪裁的实景三维模型单体化技术[1]，在原mesh模型的基础上，提取建筑，道路等地理实体平面位置，根据平面位置将地理实体从mesh网格模型中切割出来，同时对模型侧面进行平滑处理，开发了三维模型自动单体化软件。

1 总体技术路线

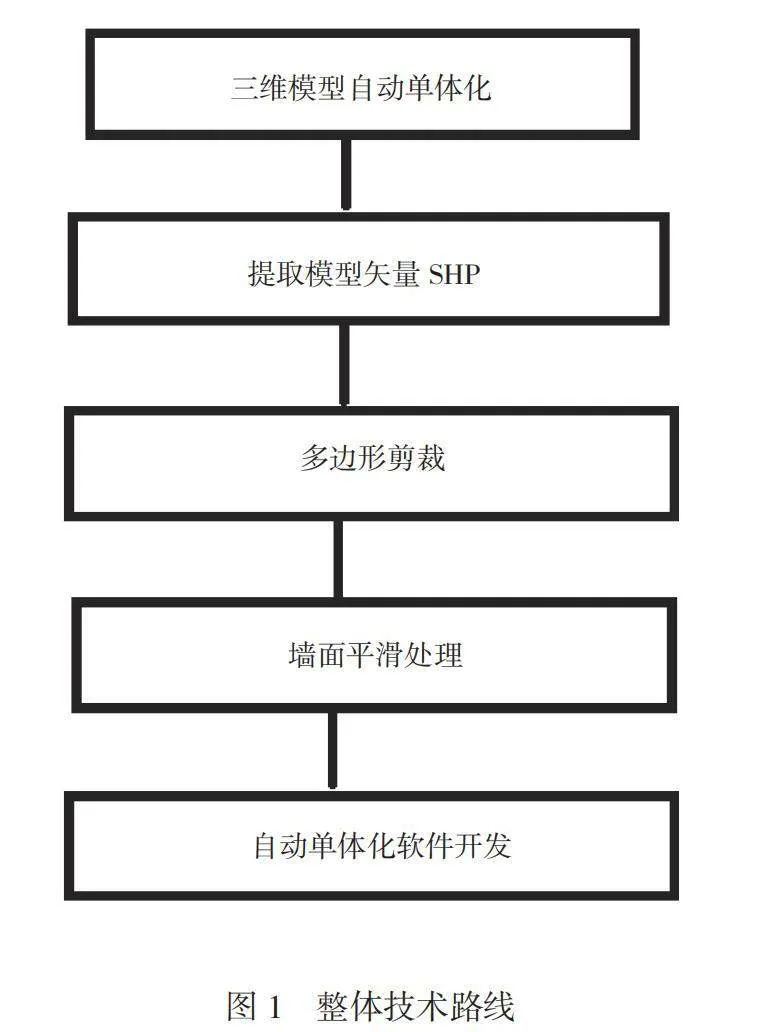
无人机在获取影像数据后，利用采集的影像的特征、相机等设备的实际参数、无人机拍摄时的定位信息，利用相关几何模型对影像数据进行几何校对。采取多幅影像联合平差的方式，解决倾斜影像之间的几何形变及互相重叠遮挡的问题。再应用多视影像密集匹配技术高效、精确地找到多幅倾斜影像中的同名点的坐标，通过获取同名点坐标将影像匹配，从而获得需要测量的地物的三维影像信息。得到高密度、真彩色的点云，在处理软件中导入数据，构建TIN三角网，建立实景三维模型。将实景三维模型导入EPS提取轮廓线，生成DWG或者SHP矢量数据。对矢量数据和三维模型进行数据叠加和多边形剪裁，将模型进行自动切割，然后将生成的模型测量纹理自动平滑，最终生成具有单体化的三维模型。整个技术路线如图1所示。

2 关键技术

三维模型自动单体化关键技术包括三角网索引、实时动态的LOD技术和多边形裁剪等。

2.1 三角网索引

三角形网格生成算法是三角网算法的基础，它根据输入的点集或线框等信息，自动构建包括三角形网格的数据结构。常用的算法包括Delaunay三角剖分、约束性Delaunay三角剖分以及Powell-Sabin三角剖分等。采用三角形网格优化算法对生成的三角形网格进行优化，提高其质量和性能[2]。本文采用优化算法包括以下3点。1）去除冗余顶点。在三角形网格中，有些顶点可能是冗余的，即它们并不贡献于网格的形状或结构。这些冗余顶点可以去除，以减少存储空间和计算时间。2）优化三角形片。在三角形网格中，有些三角形可能不是最优的，需要进行优化。例如，可以使用Loop细分、Catmull-Clark细分等算法对三角形进行细分，以提高网格质量[3]。3）修复漏洞。在三角形网格中，可能会出现漏洞或破洞，需要进行修复。常见的修复算法包括Z-order曲线、凸包法等。渲染算法各有优缺点，需要根据具体应用场景选择合适的算法。当进行渲染时，需要注意保持渲染质量和效率平衡，以便实现高效的渲染效果。最后需要进行三角形网格变换，主要是对三角形网格进行变换操作，例如旋转、缩放以及平移等。常用的算法包括齐次坐标变换、矩阵变换等。这些变换操作可以单独进行，也可以组合进行，以实现更复杂的变换效果。在进行变换操作的过程中，需要注意保持三角形网格的质量和精度，避免出现畸形或漏洞等问题。三角形网格渲染算法主要是将三角形网格转换成图像或视频等可视化形式，以便于观察和分析。常见的渲染算法包括光栅化渲染、光线追踪渲染、延迟渲染等。这些渲染算法各有优缺点，需要根据具体应用场景选择合适的算法。在进行渲染的过程中，需要注意保证渲染质量和效率的平衡，以便实现高效的渲染效果。具体实现方法如下。

文件存储格式定义：文件由3个部分组成，文件头、文件目录索引和数据。

文件头：固定长度30个Byte，前4个字节为文件版本信息（short类型），后面26个Byte为26个字符（char类型），用于存储说明性文字。

文件目录索引：目录结构整体是可变大小，但是每条目录为固定大小。

1条目录固定长度为44Byte。0～3为索引号（int类型），4～11和12～19为2个double类型。

20～27和28～35为2个double类型，是此范围的右上角点的二维坐标，36～39是此目录起始位置到此目录实际数据所在位置起点的偏移量（int类型），40～43为此目录对应数据段的三角形个数（int类型）。整个目录有1～n条目录在连续的地址中存储。将不规则三角网按照一定的范围划分为矩形网格，该网格的划分最终形成索引目录结构内容，每个网格的左下角点和右上角点为索引目录中范围数值，对所有的网格进行排序，其排序规则如下：按每个网格左下角点的X值递增排序，如果X相等，那么Y值进行递增排序。每个矩形网格中的所有三角形形成每个目录索引指向的数据段内容，它的排序规则是每个三角形的形心到此网格左下角点的角度递增排序，如果角度一致，那么按照形心到左下角点距离递增排序。

当按照上述方法将不规则三角网数据存储为外部文件后，可以使用任何编程语言对其数据进行操作处理，此处使用C++编程语言对其进行描述。程序中维护2个数据结构定义，1个是用来存储已加载到内存中的以网格为单元的不规则三角网数据，每个节点的排序方式与目录索引排序方式相同；另一个为目录索引数据，也就是网格定义的数据。因此查询输入点的高程信息的流程如下：程序在初始化阶段不加载任何三角网数据，只加载目录索引数据，程序先在索引三角形数据链表中查找此点所在范围是否已经加入内存，如果已加入内存则在该数据节点中计算高程，否则在目录索引结构中查找该点范围，将包括此点的范围数据从文件中读取并加入索引三角形数据链表中，再计算该点高程数据。

2.2 实时动态的LOD技术

本文采用动态调整LOD Scale的图像显示优化方法，具体包括以下5个步骤。1） 步骤一。根据系统帧率的指标要求，设定系统帧率可取值的最大值FRmax及最小值FRmin；获取系统当前采用的LOD" Scale值作为Scale的初始值s0，设定Scale可取值的最大值Smax及最小值Smin。2）步骤二。获取系统的当前帧率fr，如果fr＞FRmax，那么减少Scale的取值，如果当前Scale的取值不小于最小值Smin，那么以新的Scale取值作为LOD Scale渲染图像，执行步骤二；否则，若当前Scale的取值小于最小值Smin，则执行步骤三。3）步骤三。获取当前图像的当前显示细节，将所述当前显示细节与数组SC[i]中的元素逐一比较：当遍历到最后一个小于当前显示细节且与当前显示细节差值最小、同时之后的元素均不为0的元素时，停止遍历，将所述元素的编号记为n；如果n+1＜N，那么Scale值为Smin；若n=N，则Scale值Smax 以Scale值s作为LOD渲染图像，执行所述步骤三；当遍历到与当前显示细节相同的元素时，停止遍历，将所述元素的编号记为n，则Scale值s0， 以Scale取值s0作为LOD渲染图像，执行所述步骤三。当遍历到最后一个小于当前显示细节且与当前显示细节差值最小、同时之后的元素均为0的元素时，停止遍历，将所述元素的编号记为n，则Scale值s0 以Scale值s0作为LOD渲染图像，执行步骤三。4）步骤四。获取系统的当前帧率fr，若fr＞FRmax，那么减少Scale值s，若s不小于最小值Smin，则以s作为LOD" Scale渲染图像，执行步骤三；否则，执行步骤二和步骤五。若fr＜FRmin，则增大Scale值s，若s不大于最大值Smax，则以s作为LOD" Scale渲染图像，执行步骤二；否则，则执行步骤三；若FRmin≤fr≤FRmax，则执行步骤二。5）步骤五。将当前显示细节作为第i（i=（s-1）·10）个元素存入数组SC中。

2.3 多边形剪裁技术

本文采用Sutherland—Hodgman多边形裁剪算法。该算法的基本思想是每次用窗口的一条边界及其延长线来裁剪多边形的各边。多边形通常由它的顶点序列来表示，经过裁剪规则针对某条边界裁剪后，结果形成新的顶点序列，又留待下条边界进行裁剪，…，直到窗口的所有边界都裁剪完毕，算法形成最后的顶点序列，才是结果多边形（它可能构成一个或多个多边形）[4]。当多边形一个顶点Pi相对于窗口某条边界及其延长线进行剪裁时，分为下列4种情况（即裁剪规则）。1）顶点Pi在内侧，前一顶点Pi-1也在内侧，则将Pi纳入新的顶点序列。2）顶点Pi在内侧，前一顶点Pi-1在外侧，则先求交点Q，再将Q、Pi依次纳入新的顶点序列。3）顶点Pi在外侧，前一顶点Pi-1在内侧，则先求交点Q，再将Q纳入新的顶点序列。4）顶点Pi与前一顶点Pi-1均在外侧，则顶点序列中不增加新的顶点。

考虑多边形相对于一条边界及其延长线进行裁剪的算法。

2.3.1 赋初值

将顶点序列中的最后一个顶点赋给前一顶点S；

设置初始标志flag：

if（S在边界内侧）flag=0；

else flag=1；

设新的顶点序列数j=0；

2.3.2 顶点坐标求解

对多边形各顶点进行裁剪规则处理，结果放入新的多边形顶点序列Q[i][j]中：

for（对第一个顶点直到最后一个顶点，逐一处理）{if（Pi在边界内侧）{if（flag！=0）{flag=0；求交点并放入新的多边形顶点序列Qjxx；j++；}将当前顶点放入新的多边形顶点序列Qj中。

2.3.3 数据处理与试验结果

在三维景观中，就可以将需要裁剪的区域定义成掩膜，进行区域裁剪[5]。具体由下面语句来实现。

void CMyClip_AView：

：ClipedgeL（CPoint polypoint[]，CPoint clipwindow[]，UINT polynum）

/*其中参数polypoint[ ]为多边形顶点，clipwindow[]为裁剪窗口顶点，polynum为多边形顶点数目*/{//找出裁剪窗口边界

long xl，xr，yt，yb;

UINT i;

xl=clipwindow[0].x;

xr=clipwindow[0].x;

yt=clipwindow[0].y;

yb=clipwindow[0].y;

for（i=1;ilt;=4;i++）{if（xlgt;clipwindow[i].x）

xl=clipwindow[i].x;

if（xrlt;clipwindow[i].x）

xr=clipwindow[i].x;

if（ybgt;clipwindow[i].y）

yb=clipwindow[i].y;

if（ytlt;clipwindow[i].y）

yt=clipwindow[i].y;}//

CPoint B[Polygon_Num]，C[Polygon_Num];

UINT m_nA，m_nB;

int x，y;

long tem1，tem2;

m_nA=polynum;/*记载原始多边形顶点个数*/

m_nB=0;/*记载新生成多边形顶点个数*/

for（i=0;ilt;m_nA;i++）{if（polypoint[i].xlt;xl amp;amp; polypoint[i+1].xlt;xl）

{B[m_nB].x =polypoint[i].x ;

B[m_nB].y =polypoint[i].y ;

m_nB=m_nB+1;

continue;}

if（polypoint[i].xlt;xl amp;amp; polypoint[i+1].xgt;=xl）/*边两个端点起点在外部，终点在内部，求交点，然后交点，终点都应该送入临时数组*/{/*保留交点*/

x=xl;

tem1=（xl-polypoint[i].x）;

//tem2=（xl-x1）*dy/dx+y1;

//y/x=dy/dx----gt;y=x*dy/dx

tem2=tem1*（polypoint[i+1].y-polypoint[i].y）/（polypoint[i+1].x-polypoint[i].x）+polypoint[i].y;

y=tem2;

B[m_nB].x =x;

B[m_nB].y =y;

m_nB=m_nB+1;

continue;}if（polypoint[i].xgt;=xl amp;amp; polypoint[i+1].xlt;xl）/*起点在内部，终点在外，求交点，然后起点，交点送入临时数组*/

{/*保留内部点*/

B[m_nB].x =polypoint[i].x ;

B[m_nB].y =polypoint[i].y ;

m_nB=m_nB+1;

/*保留交点*/

x=xl;

tem1=（xl-polypoint[i].x）;

tem2=tem1*（polypoint[i+1].y-polypoint[i].y）/（polypoint[i+1].x-polypoint[i].x）+

polypoint[i].y;

y=tem2;

B[m_nB].x =x;

B[m_nB].y =y;

m_nB=m_nB+1;

continue;}}

//把第一个点的数据拷贝到最后

//形成裁剪后的多边形

if（i==m_nA）{B[m_nB]=B[0]；}//下------------------

m_nA=0；

for（i=0；ilt;m_nB；i++）{if（B[i].ylt;yb amp;amp; B[i+1].ylt;yb）

与Weiler-Atherton算法、Vatti算法和Greiner-Hormann算法相比，本算法采用矢量数组结构、遍历多边形顶点并记录裁剪多边形和被裁减多边形交点及其前驱、后继信息，而无须考虑输入多边形的方向、形状等，可以应对多边形边重合、边顶点相交等特殊的情况，实现多边形裁剪，并对建筑物侧面进行平滑处理。除建筑物外，采用该算法可以对路灯、井盖等地面物体进行批量单体化处理，效果良好[6]。

3 结果与讨论

结果表明，采用本多边形剪裁算法可以大幅提高工作效率，采用多边形剪裁方法能够快速、准确地提取目标对象的单体化模型。通过实景三维模型的可视化展示，能够直观地观察目标对象的单体化效果。该技术适用于不同领域的实景三维模型的单体化处理，具有广泛的应用前景。总之，基于多边形剪裁的无人机倾斜实景三维模型单体化技术是一项具有重要应用价值的研究。该技术研究能够提高实景三维模型的质量和精度，为相关领域提供更可靠的数据支持。同时，该技术具有高效性、可视化和实用性等特点，有广泛的应用前景，最终实现实景三维中国建设降本增效。

参考文献

[1]刘勇奎，高云，黄有群.一种有效的多边形剪裁算法[J].软件学报，2003（4）：845-856.

[2]蔡松露，戚正威，梁阿磊.基于GIS环境中一种高效的多边形剪裁方法[J].计算机应用与软件学，2010（3）：40-45.

[3]郭功举.面向对象的复杂多边形裁剪实现[J].现代测绘，2003，26（4）：12-15.

[4]F.COHEN，ETC.Modeling and sysnthesis of images of 3D textures"surface[J].Graphical Modeling ang Image Processing，2016（53）：501-510.

[5]GORDON PETRIE.Developments in digital photogrammetric"systems for topographic mapping application[J].ITC Journal，2017（2）：101-105.

[6]向世明.OpenGL编程与实例[M].北京：电子工业出版社，2019.