鲁棒的模糊最小二乘双参数间隔支持向量机算法

摘 要：针对最小二乘双参数间隔支持向量机（LSTPMSVM）对噪声敏感且在分类过程中易受异常值影响的问题，提出了一种鲁棒的模糊最小二乘双参数间隔支持向量机算法（RFLSTPMSVM）.该算法利用松弛变量的2范数使得优化问题具有强凸性，再根据隶属度为每个样本分配相应的权重，有效降低异常值带来的影响.同时，在目标函数中引入K-近邻加权，考虑样本之间的局部信息，提高模型的分类准确率.此外，通过求解简单的线性方程组来优化该算法，而不是求解二次规划问题，使模型具有较快的计算速度.在UCI（university of California irvine）数据集上对该算法进行性能评估，并与TWSVM、LSTSVM、LSTPMSVM和ULSTPMSVM 4种算法进行比较.数值实验结果表明，该算法具有更好的泛化性能.

关键词：双参数间隔支持向量机；孪生支持向量机；模糊隶属度；K-近邻

中图分类号：TP181"" 文献标志码：A"" 文章编号：10001565（2024）06065313

Robust fuzzy least squares twin parametric-margin support vector machine algorithm

YANG Guiyan1， HUANG Chengquan2， LUO Senyan1， CAI Jianghai1， WANG Shunxia1， ZHOU Lihua1

（1.School of Data Science and Information Engineering， Guizhou Minzu University，Guiyang 550025，China; 2. Engineering Training Center， Guizhou Minzu University， Guiyang 550025， China）

Abstract： As least squares twin parameter-margin support vector machines （LSTPMSVM） are sensitive to noise and susceptible to outliers in the process of classification， a robust fuzzy least squares twin parameter-margin support vector machine （RFLSTPMSVM） algorithm is proposed. The algorithm uses 2-norm of the slack variables to make the optimization problem strongly convex， and then assigns appropriate weights to each data sample based on the fuzzy affiliation values， which reduces the influence of outliers effectively. At the same time， the algorithm introduces K-nearest neighbour weighting into the objective function， considering the local information of samples and improving the accuracy of the model. In addition， the algorithm is optimised by solving a simple system of linear equations， rather than solving quadratic programming problems， giving the model a faster computational speed. The proposed algorithm is assessed and compared with TWSVM， LSTSVM， LSTPMSVM and ULSTPMSVM on some UCI datasets.

The numerical experiments results show that the proposed algorithm has better generalization performance.

Key words： twin parametric-margin support vector machine; twin support vector machine; fuzzy membership; K-nearest neighbor（K-NN）

收稿日期：20240606;修回日期：20240710

基金项目：

国家自然科学基金资助项目（62062024）；贵州省省级科技计划项目（黔科合基础-ZK［2021］一般342）；贵州省教育厅自然科学研究项目（黔教技［2022］015）；贵州省模式识别与智能系统重点实验室2022年度开放课题（GZMUKL［2022］KF03）

第一作者：杨贵燕（1997—），女，贵州民族大学在读硕士研究生，主要从事机器学习、模式识别等研究. E-mail：2393350042@qq.com

通信作者：黄成泉（1976—），男，贵州民族大学教授，博士，主要从事机器学习、模式识别、图像处理等研究. E-mail：hcq@gzmu.edu.cn.

支持向量机（support vector machine， SVM）^［1］由于其高泛化能力和结构风险最小化特性而广受欢迎，被应用于多个领域，如人脸识别^［2］、异常检测^［3］、医疗诊断^［4］等，但其求解二次规划（quadratic programming problem， QPP）的计算成本高，在处理复杂数据时仍有许多限制.为克服SVM存在的不足，研究者们提出了许多基于经典SVM的其他算法.拉格朗日支持向量机^［5］（Lagrangian support vector machines， LSVM）、ν-支持向量机^［6］（v-support vector machines，ν-SVM）和模糊支持向量机^［7］（fuzzy support vector machines， FSVM）是经典SVM的一些变体.

虽然支持向量机具有很高的泛化能力，但在求解过程中所耗费的计算成本较高，为解决这一问题一种称为孪生支持向量机^［8］（twin support vector machines， TWSVM）的有效方法被提出，以降低训练成本并提高泛化性能，目标是找到2个非平行的超平面，使每个超平面尽量靠近其所属类别，同时尽可能远离其他类别.在运行速度上，TWSVM算法比SVM算法大约快4倍.针对大规模数据集时，该算法效果并不佳，因此，研究人员对TWSVM进行了一些改进，以便在更短的计算时间内实现更高的分类准确性.最小二乘孪生支持向量机^［9］（least squares twin support vector machines， LSTSVM）在计算时间上得到大大提升，利用了等式约束的方式替代不等式约束来得到目标函数，与TWSVM相比速度更快.此外，双参数间隔支持向量机^［10］（twin parametric-margin support vector machine， TPMSVM）针对数据中有异方差噪声的结构的情况做了进一步优化，该算法找到了灵活的参数间隔超平面，但其仍存在计算复杂度高且易受异常值影响的问题.为了降低TPMSVM的计算复杂度，最小二乘双参数间隔支持向量机^［11］（least squares twin parametric-margin support vector machine， LSTPMSVM）试图解决TPMSVM的2个二次规划问题，用等式约束的方式求解一对线性方程组，大大减少了计算成本.由于TPMSVM采用了铰链损失函数，使得其对特征噪声敏感并且对于重采样不稳定，一种具有截断弹球损失的双参数间隔支持向量机算法^［12］（twin-parametric margin support vector machine with truncated pinball loss， TPin-TSVM）的提出解决了该问题，它可以同时保持稀疏性和特征噪声不敏感性，并且大多数正确分类的样本被给予相等的惩罚，使模型具有稀疏性.一种基于角度的双参数间隔支持向量机^［13］（angle-based twin parametric-margin support vector machine， ATP-SVM）的提出，确定了2个非平行的参数间隔超平面，以使它们的法线之间的角度最大化，可以有效地处理异方差噪声数据.基于模糊的拉格朗日双参数间隔支持向量机^［14］（fuzzy based Lagrangian twin parametric-margin support vector machine， FLTPMSVM）的提出有效减少了异常值在分类过程中的影响，通过模糊隶属度的值为每一个数据样本分配对应的权重，以此减小异常值的影响.然而，LSTPMSVM仍对噪声敏感，因此Richhariya等^［15］提出了一种新的基于universum的最小二乘双参数间隔支持向量机（universum least squares twin parametric-margin support vector machine， ULSTPMSVM），利用universum数据，引入了数据分布的先验知识，提高了模型的泛化性能.

尽管ULSTPMSVM是一种新颖的二分类算法，但由于其计算复杂度增加，对于大规模数据集存在局限性.除此之外，在分类过程中对异常值敏感且忽略了样本的局部信息，使得每个样本在构造分离超平面时共享相同的权重，事实上，它们对分离超平面有不同的影响.受ULSTPMSVM和K-近邻^［16］的启发，为了进一步提高LSTPMSVM算法的性能，本文提出了一种鲁棒的模糊最小二乘双参数间隔支持向量机算法（Robust fuzzy least squares twin parametric-margin support vector machine， RFLSTPMSVM）.在该算法中，数据样本根据其属于各自类别的程度获得模糊隶属度值.此外，与松弛变量相乘的隶属度值使得决策表面对数据集中存在的异常值和噪声不敏感.同时，通过为所有样本查找K个最近邻来考虑样本之间的局部信息，构建了一种新的非平行平面分类器.为了验证所提出的方法的有效性，在17个数据集上进行了实验，给出了RFLSTPMSVM与TWSVM、LSTSVM、LSTPMSVM和ULSTPMSVM的性能比较分析.

1 相关工作

1.1 最小二乘双参数间隔支持向量机

假设在给定的Rn空间上的训练数据集为T={（x1，y1），（x2，y2），…，（xn，yn）}，其中xi∈Rn是所输入的样本，yi∈{+1，-1}，i=1，2，…，m为样本的标签.集合T中包含m个训练样本，每个样本有n个特征，其中属于正类的样本点有m1个，属于负类的样本点有m2个，A和B分别代表维数为m1×n和m2×n的正负类样本矩阵.

最小二乘双参数间隔支持向量机试图解决TPMSVM的2个对偶问题，用等式约束代替不等式约束，简化为求解2个线性方程组，与算法TPMSVM相比，LSTPMSVM算法提高了求解效率.LSTPMSVM的优化问题为

minw1，b1，ξ12（‖w1‖2+b21）+v1eT2（Bw1+e2b1）+c12ξTξ，

s.t. Aw1+e1b1+ξ=e1，

（1）

minw2，b2，η12（‖w2‖2+b22）-v2eT2（Aw2+e1b2）+c22ηTη，

s.t. Bw2+e2b2+η=-e2，

（2）

其中：ci、vi为正参数，i=1、2;ξ、η为表示松弛变量;e1、e2表示适当维度的单位列向量.

对式（1）和式（2）中的w1、b1、w2、b2求偏导，并整理求解得到

w1b1=（c1HTH+I）^-1（c1HTe1-v1GTe2），

（3）

w2b2=（c2GTG+I）^-1（c2GTe2+v2HTe1），（4）

其中：G=［B，e2］;H=［A，e1］.

1.2 基于universum的最小二乘双参数间隔支持向量机

Richhariya等^［15］利用universum数据提出了一种新的分类算法，称为基于universum的最小二乘双参数间隔支持向量机算法.该算法在LSTPMSVM优化问题中引入数据分布的先验信息以提高模型的分类准确率.ULSTPMSVM的优化问题为

minw1，b1，η1，ξ112（‖w1‖2+b21）+v1eT2（Bw1+e2b1）+c12ηT1η1+cu2ξT1ξ1，

s.t. Aw1+e1b1=η1，

Uw1+eub1+（1-ε）eu=ξ1，

（5）

minw2，b2，η2，ξ212（‖w2‖2+b22）-v2eT1（Aw2+e1b2）+c22ηT2η2+cu2ξT2ξ2，

s.t. Bw2+e2b2=η2，

Uw2+eub2-（1-ε）eu=ξ2，（6）

其中：ci、vi、cu为正参数，i=1、2;ηi、ξi为表示松弛变量，i=1、2.

对式（5）和式（6）中的w1、b1、w2、b2求偏导，并整理求解得

w1b1=-（c1HTH+cuOTO+I）^-1（v1GTe2+（1-ε）cuOTeu，

（7）

w2b2=（c2GTG+cuOTO+I）^-1（v2HTe1+（1-ε）cuOTeu），（8）

其中：H=［A，e1］;G=［B，e2］;O=［U，eu］.

2 鲁棒的模糊最小二乘双参数间隔支持向量机

将模糊隶属度、K-近邻加权引入到最小二乘双参数间隔支持向量机（LSTPMSVM）中，并推导了在线性情况和非线性情况下的公式.

2.1 模糊隶属函数

在某些实际情况中，一些事物可能存在一种非黑即白的概念，特别是在复杂情况下，很难明确地进行归属判断，而通过隶属度值在不确定情况下做出更好的决策判断.隶属度函数可以用于评估输入样本对其所属类别的归属程度.隶属度值越高，意味着样本点对该类别的归属程度越高.本文受文献［17］的启发，将模糊函数引入到LSTPMSVM中，以下模糊函数将模糊隶属度的范围保持在（0.5，1）内.隶属函数描述为

f（xi）=1-0.5|xi-cj|rj+δ，

（9）

其中：xi为属于具有中心cj的j类的数据点；|xi-cj|表示数据点到类中心的距离，i=1、2、…、m，j=1、2；rj是距j类的数据点的类中心的最大距离，δ是一个非常小的正值，以避免被零除.

根据模糊隶属度值为不同的数据样本赋予权重，并且训练偏向于感兴趣的样本，其中隶属度值根据数据点与该类中心的距离分配.将上述模糊函数中模糊隶属度的范围选择为（0.5，1），是为了在分类器的形成中保持大多数数据点的显著贡献.此外，离群值的贡献也相应减少.

2.2 K-近邻法

在LSTPMSVM分类算法中未考虑训练样本重要性的变化，导致局部信息被忽略，意味着所有训练样本在约束函数上扮演相同的角色.因此，本文利用K-近邻^［16］来计算每个训练样本附近的紧密相邻样本的数量.

给定m个数据点x1、x2、…、xm（其中xi∈Rn来自底层子曲面M），构建一个近邻图D来模拟M的局部几何结构.对于每个数据点xi，找到其K个最近邻，并在与其近邻之间添加一条边.让N（xi）={x1i，x2i，…，xki}成为其K个近邻的集合.因此，D的权重矩阵可以定义如下：

wij=1， 如果xi是xj的K个最近邻或者xj是xi的K个最近邻，

0， 其他.

对于每个样本，都会引入一个新变量di=∑mj=1wij（i=1，2，…，m）来表示一个样本点的重要性.di值越大，表示第i个样本拥有的邻居越多，这意味着第i个样本越重要.

2.3 线性情况

在线性可分的情况下，所提RFLSTPMSVM算法所构造的2个不平行的超平面分别为f1（x）=wT1x+b1=0和f2（x）=wT2x+b2=0.线性RFLSTPMSVM的优化问题为

minw1，b1，η1，ξ212（‖w1‖2+b21）+c12ηT1D1η1+v1eT2（Bw1+e2b1）+c22（S2ξ2）TS2ξ2，

s.t. Aw1+e1b1=η1，

-（Bw1+e2b1）+ξ2=e2，

（10）

minw2，b2，η2，ξ112（‖w2‖2+b22）+c22ηT2D2η2-v2eT1（Aw2+e1b2）+c12（S1ξ1）T（S1ξ1），

s.t. Bw2+e2b2=η2，

（Aw2+e1b2）+ξ1=e1，

（11）

其中：ci、vi为正参数，i=1、2;ηi、ξi表示松弛变量，i=1、2;Si是模糊隶属度值，i=1、2;Di为一个权重矩阵，i=1、2.

分别将式（10）和式（11）中的等式约束条件代入到各自的目标函数中得到

minw1，b112（‖w1‖2+b21）+c12‖D1（Aw1+e1b1）‖2+v1eT2（Bw1+e2b1）+

c22‖S2e2+S2Bw1+S2e2b1‖，

（12）

minw2，b212（‖w2‖2+b22）+c22‖D2（Bw2+e2b2）‖2-v2eT1（Aw2+e1b2）+

c22‖S1e1-S1Aw2-S1e1b2‖.（13）

对式（12）中的w1和b1求偏导，并令其为0，得到

w1+c1ATD1（Aw1+e1b1）+v1BTe2+c2BTST2S2（e2+Bw1+e2b1）=0，

（14）

b1+c1eT1D1（Aw1+e1b1）+v1eT2e2+c2eT2ST2S2（e2+Bw1+e2b1）=0.

（15）

结合式（14）和式（15）求解，以如下矩阵形式排列：

w1b1+c1ATeT1D1［A，e1］w1b1+v1BTeT2e2+c2BTeT2ST2S2e2+［B，e2］w1b1=0.（16）

对式（16）整理得最优分类超平面为

w1b1=-（I+c1HTD1H+c2（S2G）TS2G））^-1（v1GTe2+c2（S2G）TS2e2），（17）

其中：H=［A，e1］;G=［B，e2］.

同理，对式（13）进行求解得最优分类超平面为

w2b2=（I+c2GTD2G+c1（S1H）TS1H）^-1（v2HTe1+c1（S1H）TS1e1）.

（18）

在优化式（10）和式（11）之后，算法RFLSTPMSVM在线性情况下的决策函数为

f（x）=argminw1x+b1‖w1‖，w2x+b2‖w2‖.

（19）

2.4 非线性情况

对于线性情况下不可分的情况，无法在原始空间上得到最优的分类超平面，此时使用核函数K（Xi，Xj）=（φ（Xi），φ（Xj）），将输入样本映射到更高维的特征空间中，使非线性问题转换为线性问题进行求解.2个非平行的核生成的平面分别为K（X，CT）w1+b1=0和K（X，CT）w2+b2=0，其中CT=［AT，BT］，K是适当选择的核.由此，非线性的RFLSTPMSVM优化问题如下：

minw1，b1，η1，ξ212（‖w1‖2+b21）+c12ηT1D1η1+v1eT2（K（X2，CT）w1+e2b1）+c22（S2ξ2）T（S2ξ2），

s.t. K（X1，CT）w1+e1b1=η1，

-（K（X2，CT）w1+e2b1）+ξ2=e2，

（20）

minw2，b2，η2，ξ112（‖w2‖2+b22）+c22ηT2D2η2-v2eT1（K（X1，CT）w2+e1b2）+c22（S1ξ1）T（S1ξ1），

s.t. K（X2，CT）w2+e2b2=η2，

（K（X1，CT）w2+e1b2）+ξ1=e1，

（21）

与线性情况下的求解类似，对式（20）中的w1和b1求偏导，并令其为零，即

w1+c1K（X1，CT）TD1（K（X1，CT）w1+e1b1）+v1K（X2，CT）Te2+

c2K（X2，CT）TST2S2（e2+K（X2，CT）w1+e2b1）=0

（22）

b1+c1eT1D1（K（X1，CT）w1+e1b1）+v1eT2e2+

c2eT2ST2S2（e2+K（X2，CT）w1+e2b1）=0（23）

结合式（22）和式（23）求解得到

［w1，b1］T=-（I+c1RTD1R+c2（S2F）TS2F）^-1（v1FTe2+c2（S2F）TS2e2），（24）

其中：R=［K（x1，CT），e1］；F=［K（X2，CT），e2］.

以同样的方法，对式（21）进行求解得到

［w2，b2］T=（I+c2FTD2F+c1（S1R）TS1R）^-1（v2RTe2+c1（S1R）TS1e1）.

（25）

在优化式（20）和式（21）之后，RFLSTPMSVM算法在非线性情况下的决策函数为

f（x）=argminK（X1，CT）w1+b1wT1K（C，CT）w1，K（X2，CT）w2+b2wT2K（C，CT）w2.

（26）

非线性情况下，RFLSTPMSVM算法的步骤如算法1所示.

算法1：非线性RFLSTPMSVM算法

输入：训练样本集T={（x1，y1），（x2，y2），…，（xn，yn）}，隶属度函数中的参数δ和预测样本点x.

输出：测试数据样本的类别

1）选择核函数K，利用网格搜索法，选取惩罚参数ci，vi（i=1，2），高斯核参数μ；

2）根据式（9）计算隶属度，以及使用K-近邻加权的权重矩阵；

3）根据式（20）、（21）分别求解（w1，b1）和（w2，b2）的最优解；

4）根据K（X，CT）w1+b1=0和K（X，CT）w2+b2=0构造非平行超平面；

5）使用式（26）判别样本x的所属类别.

2.5 时间复杂度分析

假设样本的总数为m，SVM的时间复杂度为O（m3），而TWSVM求解的是2个较小规模的QPP，因此计算成本约为SVM的1/4，即TWSVM的时间复杂度约为O（m3）/4.与TWSVM接近，TPMSVM算法的时间复杂度约为O（m3）/4.相较于求解二次规划问题，LSTPMSVM利用等式约束来代替不等式约束，通过求解一对线性方程组，大大减少了计算成本，所以计算成本低于TWSVM，即LSTPMSVM的时间复杂度小于O（m3）/4.由于ULSTPMSVM算法考虑了复杂的universum数据，导致计算成本增加，时间复杂度高于LSTPMSVM.与求解QPP的TWSVM相比，所提RFLSTPMSVM算法是求解线性方程组，从而降低了计算成本，时间复杂度更低.同时，由于增加了额外的模糊隶属和K-近邻的计算，使得所提RFLSTPMSVM的时间复杂度略高于LSTPMSVM.

3 实验结果与分析

为了评估针对二分类任务提出的RFLSTPMSVM算法的性能，将所提算法与TWSVM、LSTSVM、LSTPMSVM和ULSTPMSVM进行性能比较分析.

3.1 数据集

本文在来自UCI机器学习知识库^［18］的17个真实世界数据集上进行实验，数据集的相关信息如表1所示.

3.2 实验装置

所有实验均是在使用Windows 10操作系统64位、3.40 GHz英特尔酷睿i7-3700处理器、8 GB内存和MATLAB R2020a环境的PC上进行的.为了使结果更具说服力，本文所提算法和所有对比算法进行了5重交叉验证，利用网格搜索法^［19］以获得最佳超参数.对于UCI数据集上的实验，50%的数据用于训练.在本实验中，使用高斯核实现了非线性情况下的所有方法，该高斯核由下式给出：

K（xi，xj）=exp-‖xi-xj‖22σ2.

（27）

算法RFLSTPMSVM对比算法TWSVM、LSTSVM、LSTPMSVM和ULSTPMSVM中所涉及的惩罚权重的正则化参数c1、c2、v1、v2参数选择范围为{10^-5，10^-4，…，10⁴，10⁵}，高斯核参数μ的选择范围为{2^-5，2^-4，…，2⁴，2⁵}.

3.3 实验结果

下面通过实验来验证RFLSTPMSVM算法的有效性.用训练时间和准确率（ACC）作为所有算法的分类性能的评估标准，准确率的计算公式如下：

ACC=TP+TNTP+FP+TN+FN，

（28）

其中TP、TN、FN、FP分别表示正确分类的正类样本数、正确分类的负类样本数、错误分类的负类样本数以及错误分类的正类样本数.

为了验证所提算法的性能，在17个数据集上做了线性情况和非线性情况下的实验比较.图1给出了线性情况下5种算法的分类准确率情况.由图1可以看出，所提RFLSTPMSVM算法在Ecoli-0-2-6-7_vs_3-5、Ecoli-0-3-4-6_vs_5、yeast3、segment0等12个数据集上有最高的分类准确率，在其他数据集上也有和对比算法相当或更好的表现.

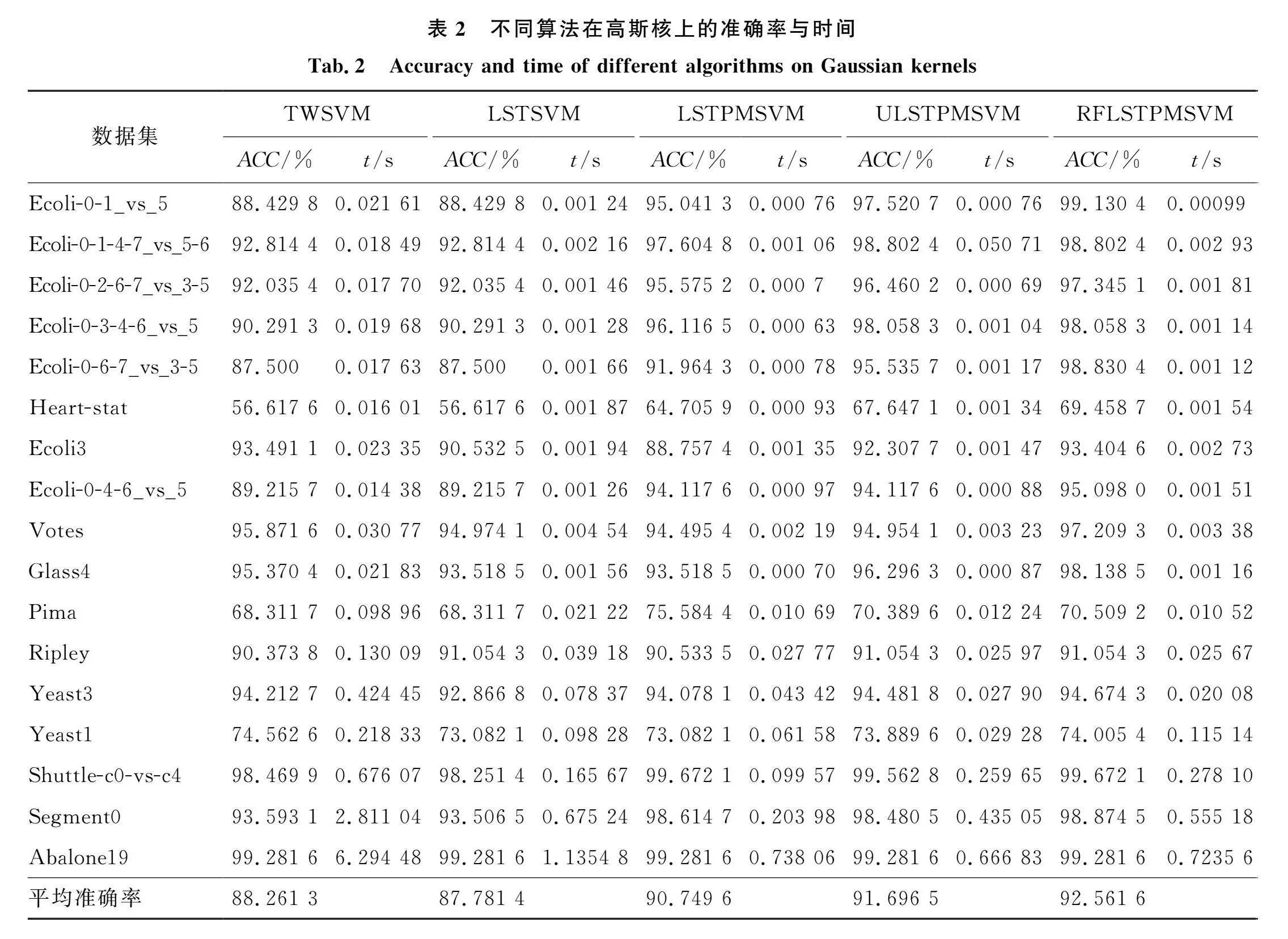
表2列出了非线性情况下5种算法的分类准确率和训练时间.从训练时间看，TWSVM算法的时间是最长的，这是因为与其他4种基于最小二乘的算法中的线性方程组相比，TWSVM的求解涉及一对二次规划问题，更耗时.而本文提出的RFLSTPMSVM算法需要花费的训练时间与LSTSVM、LSTPMSVM和ULSTPMSVM算法相当或更长，这是由于本文的模型中使用K-近邻法加权利用样本的类内局部信息和模糊隶属度值增加了额外的计算.就分类准确率而言，由表2可以看出，在非线性情况下，所提算法RFLSTPMSVM在17个数据集上有13个的准确率是最佳的，并且在没有获得准确率最优的数据集上表现也与其他算法相当或者更好，尤其是在数据集Ecoli-0-1_vs_5、Ecoli-0-6-7_vs_3-5和Glass4中，与其他对比算法的最佳结果相比，RFLSTPMSVM的准确率提高了1.60%、2.52%和1.84%.同时在Pima数据集上，LSTPMSVM的表现最好，准确率达到了75.5844%.并且RFLSTPMSVM在Ripley、segment0、abalone19等6个相对规模较大的数据集上，有4个数据集获得了最高准确率，并且数据集Abalone19上5种算法的准确率一样.可见与已有的算法相比，所提算法在较大规模数据集上的分类效果较好.

表2的最后一行计算了5种算法的平均准确率，可以看到所提算法RFLSTPMSVM的平均准确率是最高的.综合平均准确率来看，RFLSTPMSVM相较于其他对比算法，分别提高了 4.3%、4.78%、1.8%、0.87%，说明了本文算法的有效性.总体来说，RFLSTPMSVM算法在多数情况下优于其他算法，因此，本文所提算法在一定程度上提高了模型的泛化能力.实验结果表明，将模糊函数和K-近邻引入到最小二乘双参数间隔支持向量机中，能得到较好的分类结果.

为了检测RFLSTPMSVM算法的抗噪性能，在每个数据集上分别加入了5%、10%、15%和20%的噪声，并在5种算法上进行了实验，得到实验结果如图2所示.由图2可以看出，在添加4种不同比例的噪声之后，5种算法的分类准确率都有一定的变化.因为噪声的存在导致了数据样本分布变得混乱，使得两类样本的边界变得不明确，从而引起超平面的偏移，分类准确率有所变化.同时可以看到TWSVM和LSTSVM在部分数据集上准确率没有变化，相对来说有更好的稳定性，但整体分类准确率并不高.而RFLSTPMSVM则表现出较为稳定的性能，并在大多数数据集上的准确率优于其余对比算法.

在Pima数据集上，没有添加噪声时，RFLSTPMSVM的分类准确率低于LSTPMSVM，但在加入添加噪声之后，其准确率超过了所有对比算法.在Ecoli-0-3-4-6_vs_5数据集上，无噪声情况下和添加5%噪声时，RFLSTPMSVM和ULSTPMSVM的分类准确率一样，而随着噪声不断增加，RFLSTPMSVM的分类准确率高于ULSTPMSVM.总体来看，当添加噪声至20% 时，RFLSTPMSVM在4个数据集上分类准确率在所有算法中表现最佳，实验表明所提RFLSTPMSVM算法具有一定的抗噪性能.

3.4 统计分析

从表2中可以看出，所提算法的分类准确率并没有在所有数据集上都优于对比算法.为了进一步评估，采用统计分析对5种算法对实验结果进行Friedman检验^［20］.在Friedman检验中，每个分类器在每个数据集上都被分配了1个等级，表现较差的分类器将获得较高的等级，反之亦然.Friedman检验统计量的计算如下：

χ2F=12Nk（k+1）∑kj=1R2j-k（k+1）24，（29）

其中：N表示数据集的数量;k表示算法的数量;Rj表示在第j个分类器上的平均等级.由于弗里德曼的χ2F过于保守，采用了一个更好的统计量FF来分析，FF是服从自由度为（k-1）和（k-1）（N-1）的分布，FF分布为

FF=（N-1）χ2FN（k-1）-χ2F.（30）

为此，计算了非线性情况下5种算法的平均等级，得到结果如表3所示，其中等级是根据分类准确率计算的.由表3可以看到，TWSVM、LSTSVM、LSTPMSVM，ULSTPMSVM和RFLSTPMSVM算法的平均等级分别为3.66、4.32、3.23、2.42和1.44.在Friedman检验中，假设在零假设下每种算法的平均等级相等，并且表现出相似的性能.根据式（29）和式（30）计算各算法的平均等级计算χ2F和FF值得到

χ2F=12×175（5+1）∑5j=1R2j-5（5+1）24=

12×175（5+1）3.662+4.322+3.232+2.422+1.442）-5（5+1）24≈36.845 9，

FF=（17-1）×36.845 817×（5-1）-36.845 8≈18.923 1.

F（4，64）的临界值在显著性水平时为2.515，FF值远大于临界值，所以拒绝零假设，说明5种算法之间存在显著差异.并且从表3中平均等级排名可以看出，所提出的模型在非线性情况下具有最低的平均等级，显示了其优越的性能，结果表明RFLSTPMSVM优于TWSVM、LSTSVM、LSTPMSVM和ULSTPMSVM算法.

采用Nemenyi事后检验对模型进行成对差异比较.根据Nemenyi检验，如果2个模型的平均等级差异大于临界差异，则它们存在显著差异，其中临界差异（CD）的计算公式为

CD=qαk（k+1）6N.（31）

在非线性情况下，对于在α=0.05的显著性水平下，计算得到算法之间的平均等级至少应该相差临界值CD（1.48）.由表3之间的平均等级可知，RFLSTPMSVM与TWSVM、LSTSVM、LSTPMSVM、ULSTPMSVM之间的差值均大于CD值1.48，但与ULSTPMSVM算法之间的差值小于CD值1.48.非线性情况下RFLSTPMSVM与不同算法之间的成对差异结果如表4所示.结果表明，所提算法RFLSTPMSVM与TWSVM、LSTSVM、LSTPMSVM算法之间的性能在统计上是存在明显差异的，而与ULSTPMSVM算法之间的差异在统计上不显著.

3.5 不敏感性分析

为了分析超参数值对所提RFLSTPMSVM算法的准确率的影响，本文选取了2个数据集Votes和glass4进行不敏感性分析.图3显示了RFLSTPMSVM在2个数据集上参数的准确率变化.

图3中cvs1表示参数c=c1=c2，muvs表示高斯核参数μ.对于数据集Votes（图3a），当参数c的值为最小值10^-5时，RFLSTPMSVM的准确率最低，随着c值的增大，参数μ也逐渐增大时，RFLSTPMSVM的准确率随着上升，并且趋于一个稳定值.对于数据集glass4（图3b），当参数c的值为最小值10^-5时，RFLSTPMSVM的准确率达到最低.随着c值逐渐增大，参数μ不管怎么变化，RFLSTPMSVM的准确率趋于一个稳定值.当c值为104，μ值为22时，RFLSTPMSVM的准确率达到最大值96.296 3.

4 结语

提出了一种鲁棒的模糊最小二乘双参数间隔支持向量机算法（RFLSTPMSVM）用于二分类问题.通过将模糊隶属度值引入训练数据样本，并将松弛变量的2范数平方与隶属度值相乘，使所提算法对数据中存在的异常值和噪声变得不敏感.同时，在目标函数中利用样本的局部信息加权，使每个样本在构造分离超平面时根据其重要性获得相应的权重，有效提高预测精度.此外，所提RFLSTPMSVM具有灵活的参数间隔超平面，使其适用于异方差结构.在17个数据集上的数值实验验证了RFLSTPMSVM的可行性和有效性.从本文提供的性能比较分析可以看出，与其他已有4种算法相比，RFLSTPMSVM提供了相当或更好的分类准确率，具有更好的泛化性能.但该算法只涉及到二分类问题，因此，将二分类问题扩展到多分类问题是下一步的主研究方向.

参 考 文 献：

［1］ CORTES C， VAPNIK V. Support-vector networks［J］. Mach Learn， 1995， 20（3）： 273-297. DOI： 10.1007/ bf00994018.

［2］ SUBUDHIRAY S， PALO H K， DAS N. Effective recognition of facial emotions using dual transfer learned feature vectors and support vector machine［J］. Int J Inf Technol， 2023， 15（1）： 301-313. DOI：10.1007/s41870-022-01093-7.

［3］ PANG J X， PU X K， LI C G. A hybrid algorithm incorporating vector quantization and one-class support vector machine for industrial anomaly detection［J］. IEEE Trans Ind Inform， 2022， 18（12）： 8786-8796. DOI：10.1109/TII.2022.3145834.

［4］ YI L， XIE G J， LI Z H， et al. Automatic depression diagnosis through hybrid EEG and near-infrared spectroscopy features using support vector machine［J］. Front Neurosci， 2023， 17： 1205931." DOI：10.3389/fnins.2023.1205931.

［5］ MANGASARIAN O L， MUSICANT D R. Lagrangian support vector machines［J］. J Mach Learn Research， 2001， 1（Mar）： 161-177. DOI：10.1162/15324430152748218.

［6］ SCHLKOPF B， SMOLA A J， WILLIAMSON R C， et al. New support vector algorithms［J］. Neural Comput， 2000， 12（5）： 1207-1245. DOI：10.1162/089976600300015565.

［7］ LIN C F， WANG S D. Fuzzy support vector machines［J］. IEEE Trans Neural Netw， 2002， 13（2）： 464-471. DOI：10.1109/72.991432.

［8］ JAYADEVA， KHEMCHANDANI R， CHANDRA S. Twin support vector machines for pattern classification［J］. IEEE Trans Pattern Anal Mach Intell， 2007， 29（5）： 905-910. DOI：10.1109/ TPAMI. 2007.1068

［9］ ARUN KUMAR M， GOPAL M. Least squares twin support vector machines for pattern classification［J］. Expert Syst Appl， 2009， 36（4）： 7535-7543. DOI：10.1016/j.eswa.2008.09.066.

［10］ PENG X J. TPMSVM： a novel twin parametric-margin support vector machine for pattern recognition［J］. Pattern Recognit， 2011， 44（10/11）： 2678-2692. DOI：10.1016/j.patcog.2011.03.031.

［11］ SHAO Y H， WANG Z， CHEN W J， et al. Least squares twin parametric-margin support vector machine for classification［J］. Appl Intell， 2013， 39（3）： 451-464. DOI：10.1007/s10489-013-0423-y.

［12］ WANG H R， XU Y T， ZHOU Z J. Twin-parametric margin support vector machine with truncated pinball loss［J］. Neural Comput Appl， 2021， 33（8）： 3781-3798. DOI：10.1007/s00521-020-05225-7.

［13］ RASTOGI NéE KHEMCHANDANI R， SAIGAL P， CHANDRA S. Angle-based twin parametric-margin support vector machine for pattern classification［J］. Knowl Based Syst， 2018， 139： 64-77. DOI：10.1016/j.knosys. 2017.10.008.

［14］ GUPTA D， BORAH P， PRASAD M. A fuzzy based Lagrangian twin parametric-margin support vector machine （FLTPMSVM）［C］//2017 IEEE Symposium Series on Computational Intelligence （SSCI）， Honolulu， HI， USA. IEEE， 2017： 1-7. DOI：10.1109/SSCI.2017.8280964.

［15］ RICHHARIYA B， TANVEER M. Universum least squares twin parametric-margin support vector machine［C］//2020 International Joint Conference on Neural Networks （IJCNN）， Glasgow， UK， IEEE， 2020： 1-8. DOI： 10.1109/IJCNN48605.2020.9206865.

［16］ TANVEER M， SHUBHAM K， ALDHAIFALLAH M， et al. An efficient regularized K-nearest neighbor based weighted twin support vector regression［J］. Knowl Based Syst， 2016， 94： 70-87. DOI： 10.1016/j.knosys.2015.11.011.

［17］ RICHHARIYA B， TANVEER M， FOR THE ALZHEIMER’S DISEASE NEUROIMAGING INITIATIVE. A fuzzy universum least squares twin support vector machine （FULSTSVM）［J］. Neural Comput Appl， 2022， 34（14）： 11411-11422. DOI：10.1007/s00521-021-05721-4.

［18］ DUA D， TANISKIDOU E K. UCI machine learning repository， 2017［DB/OL］.［2022-10-16］. http：//archive. ics. uci. edu/ml/.

［19］ 刘小生， 章治邦.基于改进网格搜索法的SVM参数优化［J］.江西理工大学学报， 2019， 40（1）： 5-9. DOI： 10.13265/j.cnki.jxlgdxxb.2019.01.002.

［20］ BENAVOLI A， CORANI G， DEMSAR J， et al. Time for a change： a tutorial for comparing multiple classifiers through Bayesian analysis［J］. J Mach Learn Research， 2017， 18（77）： 1-36. DOI：10. 48550/arXiv.1606.04316.

（责任编辑：孟素兰）