小学数学低段课程游戏化的案例与思考

2022年版课标指出，为了加强学段衔接，要合理设计小学一至二年级课程，注重活动化、游戏化、生活化的学习设计。游戏化是指在非游戏情境中使用游戏元素和游戏设计[1]。游戏元素是指构成游戏的基本要素，如游戏道具、游戏规则、反馈评价等。游戏设计主要指游戏规则的制定。课程游戏化，就是在课程内容的教学过程中使用游戏元素和游戏设计。通过游戏的形式学习数学知识，能够有效激发学生学习的内在动力，使他们在玩中体验并获得知识，将从游戏中获得的快乐体验转化为深层的知识与能力获得的满足感，对数学学习产生兴趣并树立信心，进而落实课程目标，发展核心素养。如图1所示是课程游戏化的设计流程。

一、课程游戏化的实例

（一）课程内容。

下面以小学数学第一学段立体图形的认识为例，进行游戏化设计。2022年版课标提出的相关内容要求是：通过实物和模型辨认简单的立体图形，并在图形的认识过程中，形成初步的空间观念。学业要求具体是：能辨认长方体、正方体、圆柱、球等立体图形，能直观描述这些立体图形的特征。教学提示为：图形的认识教学以直观感知为主，选用学生身边熟悉的素材，鼓励学生动手操作，引导学生经历图形的抽象过程，积累观察物体的经验，形成初步的空间观念。通过分析，我们设计了直观感知图形的特征并形成初步的空间观念的课程内容。

（二）课程目标。

认知学习目标：能直观地描述长方体、正方体、圆柱、球这四种立体图形的特征，并能在具体情境中辨别这些立体图形。

动作技能目标：从不同角度观察并触摸立体图形，在多种感官参与的基础上，初步建立不同立体图形的表象。

情感学习目标：在积极、主动学习的过程中，积累认识图形的活动经验，对图形的学习产生浓厚的兴趣。

（三）游戏规则。

基于课程目标，我们设计了“几何迷阵”这一游戏化教学活动。它由棋子、棋盘和提示数字这三部分组成。有两条游戏规则：一是每行、每列都不能有相同的立体图形，二是棋子的摆放要符合提示数字要求的遮挡关系。将棋子按规则摆满棋盘，即完成任务。

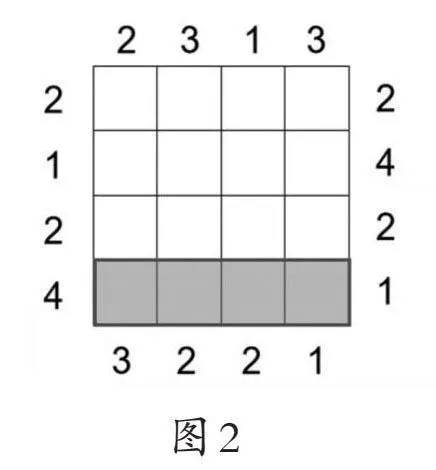
以4阶棋盘为例。它是由16个小正方形组成的大正方形。与之配套的棋子是16个，具体包括4个完全相同的球、4个完全相同的正方体、4个完全相同的圆柱、4个完全相同的长方体。如图2所示，四周显示的数字是提示数字。以第4行（图2中阴影部分）为例。左边显示的数字是4，则要求在从左往右的水平方向观察时，能够同时观察到4种立体图形，如图3所示。右边的提示数字是1，则要求在从右往左的水平方向观察时，只能看到1种立体图形，其余的均被遮挡住，如图4所示。如图5所示就是棋盘中第4行棋子的排列顺序。

（四）道具制作。

为了满足遮挡关系，在制作立体图形时需要注意：长方体要能将其余3种立体图形全部遮挡住，圆柱要能遮挡住正方体和球，正方体要能遮挡住球。另外，注意把4种棋子的颜色区分开。所有的棋子以“袋”为单位，进行特殊定制。例如，在制作球时，将1袋超轻黏土平均分成4份，做成4个球；将2袋超轻黏土混合，再平均分成4份，做成4个正方体；将3袋超轻黏土混合，再平均分成4份，做成4个圆柱；将6袋超轻黏土混合，再平均分成4份，做成4个长方体。还要注意的是，不要将圆柱和长方体做得太高，否则很难平稳摆好。

（五）游戏环节。

环节1：小试牛刀。

学生需要独立完成3阶几何迷阵，棋子是3个长方体、3个圆柱和3个正方体，棋盘及提示数字如图6所示。学生根据提示数字从不同方向观察，并结合“每行、每列都不能有相同的立体图形”摆放棋子。如图7所示是摆好的几何迷阵。

环节2：合作闯关。

4名学生合作完成4阶几何迷阵，棋子是16个立体图形，棋盘和提示数字如图2所示。4名学生需要分别站在4个不同的方向同时观察并摆放棋子，这样做的目的是降低学生完成几何迷阵的难度，同时培养学生的合作意识。如图8所示是摆好的几何迷阵。

环节3：终极挑战。

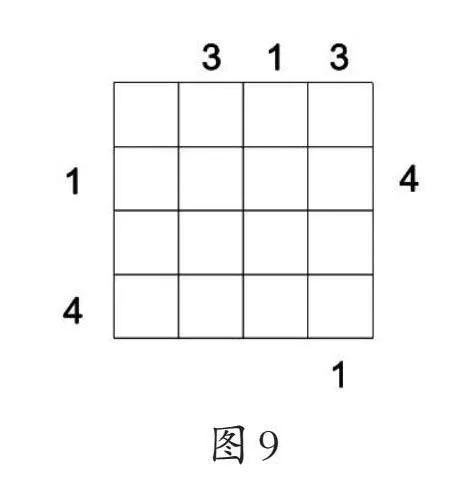
学生需要独立完成4阶几何迷阵，谜题如图9所示。它是在环节2中的谜题的基础上去掉9个提示数字构成的。该谜题只提供了7个提示数字，这就要求学生将游戏的两条规则结合起来进行推理。最终的摆放结果与环节2中的摆放结果一致。

（六）反思提升。

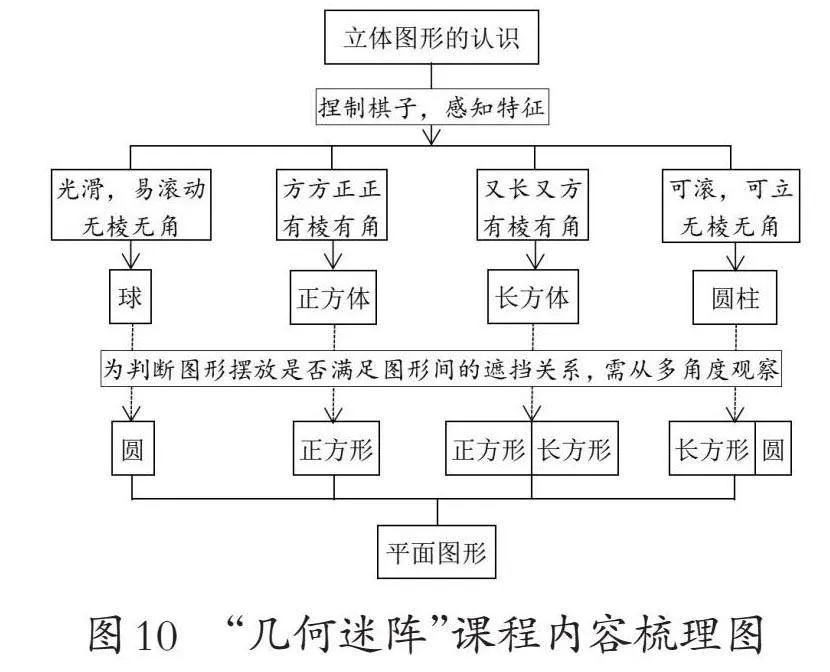
首先，梳理其中蕴含的课程内容，如图10所示。在捏制立体图形的过程中，感受图形的特征。学生从不同角度观察立体图形，能够更好地体会面在体上、体由面组成。同时，活动经验可以迁移到观察物体和三视图的学习中。

其次，分享游戏经验，培养推理能力和统筹协调能力。在学生经历了多次探索过程后，要引导学生进一步思考：“你觉得应该先摆哪一行或者哪一列？为什么？”例如，学生发现由提示数字4能够直接确定4种立体图形的排列顺序，可以优先摆放；而由提示数字1能直接确定长方体的位置等。

二、课程游戏化的意义

（一）能使学生更充分地积累活动经验。

课程游戏化的活动过程中，学生能够实现多感官参与，进而能更充分地积累活动经验。例如，学生发现球是最好制作的立体图形，却是制作次数最多的图形，因为球总是会“偷偷跑掉”，学生在这样的经历中切实感受到球会随意滚动的特征。在游戏环节，学生需要不停摆放这些立体图形，在手触摸的过程中感受不同立体图形的特征。同时由于眼睛需要一直观察，看的过程中能够促进立体图形的表象在脑海中形成，在积累认识图形的活动经验的同时发展空间观念。

（二）能更有效地激发学生的学习动机。

课程游戏化通过设置富有挑战性的任务、及时反馈、等级评价等游戏元素，能有效激发学生参与的内在动力。例如，学生学习了4种立体图形，就可以设置3阶、4阶的几何迷阵游戏。后续学习了更多的立体图形后，就可以设计5阶、6阶甚至更多阶的几何迷阵游戏。此外，同一阶的几何迷阵可以有丰富的谜题，并且谜题的数量会随着阶数的增加变得丰富多彩。由此，就可以设计不同难度的关卡，通过及时反馈，引领学生不断挑战更难的任务，激发学习动机。

（三）能促使学生更主动地学习课程。

课程游戏化让学生通过游戏这一快乐的学习形式，最终体会到知识与能力获得的满足感，学生将会被数学本身深深吸引，进而能更主动地学习课程内容。例如，学生发现长方体是最难捏的立体图形，不过可以借鉴捏正方体的经验，这样学生对长方体和正方体之间的关系就有了初步的感知，并且在捏制过程中“棱角”“相对的面”等一些专业词语竟然被学生自然而然地创造出来。还有学生发现，明明黏土的量是相同的，可是捏出的圆柱“长”得并不一样，有的“矮胖矮胖”，有的“瘦高瘦高”，这样的思考让学生初步感知到圆柱的体积相同时，其底面积与高之间的关系。本来很抽象的数学知识，此时变得生动活泼，同时深深吸引着学生更加主动地去探究。

参考文献：

[1]尚俊杰，裴蕾丝.重塑学习方式：游戏的核心教育价值及应用前景[J].中国电化教育，2015（5）.

【本文系北京市教育科学“十四五”规划2021年度一般课题“基于大单元教学的学科实践活动课程设计与实施研究”（编号：CDDB21436）的研究成果】

（作者单位：北京市顺义区建新小学） Y