历史相似性视角下“圆的认识”两种学习路径的思考与实践

随着HPM（History and Pedagogy of Mathe-matics，数学史与数学教育）研究工作的深入，历史相似性原理正逐渐为广大中小学教师所接受并付诸教学实践。历史相似性的实证研究具有重要意义，不仅能够清晰地还原数学的演进历程，深刻地揭示火热的历史动因，而且可以有效地帮助学生跨越学习数学的认知障碍，为数学教学改革提供宝贵的历史经验[1]。在教学实践中，历史相似性能为教学设计与实施提供知识、素材、方法和路径的支持。然而，在一些活动中，教师只关注数学史作为知识、素材的一个侧面，数学史及其历史相似性的价值有待进一步挖掘。为此，笔者以“圆的认识”一课为例，在分析、思考的基础上，开展了教学实践。

一、“圆的认识”中的历史相似性

（一）历史相似性在教学中的应用。

近年，中国HPM研究团队基于历史研究、调查研究等方法，实证了历史相似性的客观存在[1]。有研究者认为，对于历史相似性在教学中的应用，相较于局部相似，更应该倡导整体相似的研究思路，也就是以数学史专业研究的已有成果为基础，从整体上研究把握数学发展某一方面的历史脉络，教学设计追求历史认识过程与学生认知过程整体上的某些相似性[2]。因此，整体相似意味着某一数学内容的历史发生过程与当下学生的认知过程在主要节点存在相似性，并不代表其顺序、内容完全一致。教学中不需要完全复制历史进程，而应对其中有研究价值的重点和难点问题进行充分探讨。此外，还应挖掘历史进程与学生认知之间的关系，根据学生的已有水平，设计不同的学习路径与活动，促进学生思维水平的提升。

（二）群体相似性及其实例。

除了重要节点的相似，在实际教学中，整体相似另一个层面的含义体现为群体相似性，即同一时间段内，学生群体中不同水平层次的个体对同一教学内容的认知会与历史上各个不同阶段大致对应。以“圆的认识”为例，早期人类对圆的认识经历了“模仿—操作—比较—思辨”的过程。人们对太阳、月亮、水波、木桩等自然事物或现象进行观察，模仿其外形制作圆形物品。例如，打磨圆形石块、制作圆形陶碗。随后，在操作过程中，人们概括出了圆的要素，并尝试制作画圆的工具。例如，在用尖利的石块钻孔的过程中，发现了圆心和直径（半径），从而发明了简易的画圆工具并将其逐步改进成圆规[3]。在此基础上，人们尝试从方与圆之间的关系来研究圆。例如，古埃及人分别在正方形和圆中铺满谷子来研究两者的面积之比[4]；阿基米德等古希腊数学家通过圆的内接和外切正方形来研究圆；刘徽、祖冲之等从圆内接正六边形出发，利用割圆术来研究圆。在模仿、操作、比较、思辨的同时，人们尝试给圆下定义，如我国古代典籍《墨经》和古希腊数学代表作《几何原本》中都给出了圆的定义。时至今日，学生在面对相关问题时会有怎样的表现呢？在一个给出简单工具（皮筋、回形针、工字钉、线、三角尺、直尺、纸条），要求用尽可能多的方法画圆的小调查中，六年级学生在画圆工具和方法的选择方面，呈现出一定的个体特征。将选用同种方法的个体分成若干个小群体，这些小群体的表现几乎都能与早期历史上的主要研究进程形成对应关系，如图1所示。

（三）学生不同表现的借鉴意义。

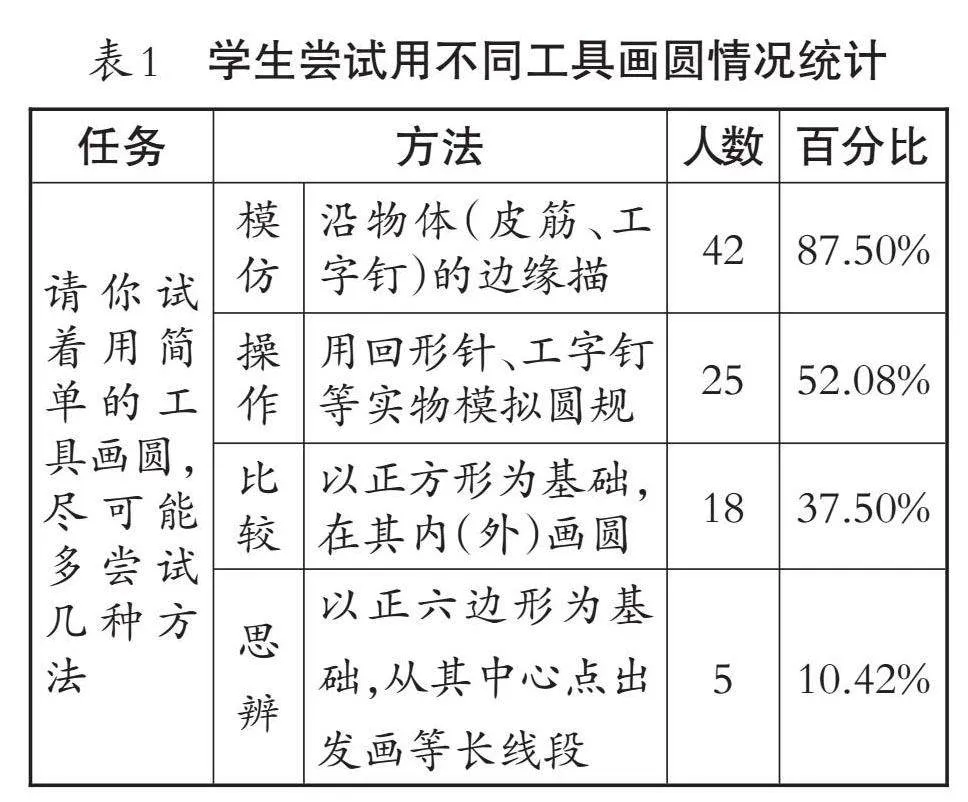
如表1，学生在画圆时，呈现出模仿、操作、比较和思辨这四种不同的方式。出于方便等原因，沿着圆形物品的边缘描出圆是大多数学生的首选。但这一方法显然满足不了六年级学生的求知欲，约52.08%的学生在描画的基础上找到了更加合适的工具和方法，借助简单的工具形成圆心和半径，较为准确地画出了圆，这一方法是站在解决问题的角度加以思考得到的。37.50%的学生还尝试从数学对象本身及其相互之间的关系进行理性思考。例如，在正方形的基础上画圆，或用三角形拼组的方式画圆。还有约10.42%的学生借助刻度尺，根据正多边形与圆的联系与区别，以正六边形为基础，从其中心点出发画等长线段作为半径，连接半径的另一个端点形成圆，这与《墨经》中圆的定义一致。不同的画圆方法对应不同的历史研究进程，也反映出学生对圆的不同认知方式和思维水平，这为设计不同的学习路径创设了条件。

二、基于历史相82ebbd47de8ea8e6035a9dec90ad2adae1e08eab7ea6a0f21b61e824b33404e7似性的两种学习路径

结合圆的历史研究进程与学生的认知水平，“圆的认识”一课至少有两种学习路径。

一是基于问题解决（用简易工具画圆），从实践方法中发现并概括圆的要素和特征。这是一种以归纳为主的学习路径，主要包括：尝试根据提供的简单工具画圆，展示作品并相互评价；比较不同画法的优点和缺点，提出改进意见并再次尝试画圆；总结用不同工具画圆的共同之处，体会画圆的要点；概括圆的两大要素——圆心和半径，发现半径的特点。

二是根据对方与圆两者之间关系的思辨，在正多边形和圆的比较中（主要是中心点到边的距离），通过类比的方式将圆纳入已有的平面图形体系中。这一学习路径体现了同化思想，主要包括：观察比较，整体感知正六边形、正十二边形与圆之间的关系；尝试以正六边形为基础画出正十二边形，讨论画等长线段的方法，猜想继续画会得到什么图形；观察等长线段的端点围成的图形（圆），讨论与圆规画圆的异同；解读圆的概念，体会方与圆之间的关系，借助割圆术感受极限思想。

三、两种学习路径的教学实践与分析

（一）学习路径一：操作简易工具画圆，归纳共性形成概念。

人们对圆的特征的研究贯穿于对圆的观察、描摹和运用工具画圆的过程中。学生经历类似的过程，有助于在实践经验总结概括的基础上，形成圆的概念，把握圆的要素及其特征。

课始，教师出示古巴比伦泥板上近似于圆的图形，并请学生猜猜当时的人们可能是怎样画圆的。随后，请学生借助简易工具（皮筋、回形针、工字钉、棉线、纸条等）尝试画圆。学生独立完成后上台演示并介绍自己的画圆工具、方法和结果。通过演示，学生发现沿着皮筋里面一圈描时，皮筋是软的而且容易移动，因此画不圆。如果把皮筋套在工字钉上，再套上铅笔拉紧后旋转，也会因为皮筋的长度易变化而画不圆。而改用回形针代替皮筋，则可以避免因弹性而导致长度不一致的问题，按上述方法就可以画出圆。也有学生用棉线或纸条代替回形针画出了更大的圆。

教师引导学生对刚才成功或失败的案例进行比较和分析，从中概括出画圆的要点及圆的要素。学生认为画圆时先要有一个固定的中心点，且笔尖到中心点的距离必须保持不变。教师肯定学生的想法，并指出在数学上这个中心点就是圆心，这个不变的距离叫作半径。随后请一名学生上台示范找出已知圆的圆心和半径的方法，并请其他学生表达看法。学生发现在一个圆内可以画无数条半径，因为半径是圆心和圆上的点相连而成的线段，圆上的点有无数个，半径就有无数条，并且同一个圆的半径都相等。

最后，教师出示《墨经》中的“圆，一中同长也”，以及《几何原本》中的“圆是由一条线围成的平面图形，其内有一点与圆上的点连接所成的所有线段都相等”。学生通过理解与对比，发现这两种描述都涉及圆心与半径这两个核心要素。至此，学生已经对圆心和半径及其重要性有了深刻的认识[5]。

（二）学习路径二：整体类比感知联系，猜想验证概括特征。

我国古代广为流传的“天圆地方”观念，不论是从客观现象还是意识形态的角度，都说明人们对方与圆两者之间关系的思辨。在“图形与几何”领域，这是一个重要的内容，阿基米德和刘徽等人的研究就是很好的例证。同时，这是学生非常容易接触到并能引发关注和思考的话题。

教学开始，教师分别呈现正六边形、正十二边形，再逐渐增加边数，最后呈现圆，使学生整体感知其中的变化过程和各图形间的相互关系。随后，请学生以正六边形为基础，画出正十二边形。教师展示学生的两种画法，即在正六边形外围画十二条线段和以正六边形的中心点为端点画六条垂直于边的等长线段，再比较哪种方法更合理。经过讨论，学生普遍认为后者更加严谨、规范。在得出结论之后，请学生猜想：继续画这样的等长线段，可能得到什么图形？学生在提出猜想后继续作图并总结：按照这样的方法，等长线段越多，正多边形的边也就越多，就越接近圆。当这样的线段有无数条时，无数个端点的连线就形成了圆。随后，教师请学生对比正六边形和圆，说说它们的异同点。学生认为两者的共同点是都有中心点和等长线段，但正六边形中这样的等长线段只有六条，而圆中则有无数条。

在感知、操作、猜想、验证、想象、类比等活动的基础上，教师出示《墨经》中的“圆，一中同长也”，请学生结合活动经验说说对这句话的理解，随后给圆心和半径命名。有了这些活动的支持，圆中原本隐藏的圆心与半径这两大要素及半径的特征不言自明，学生对圆的概念的理解也就水到渠成了。最后，教师介绍刘徽的割圆术，帮助学生梳理整个研究过程，并借此渗透极限思想，使学生认识到正多边形与圆之间可以相互转化是一个明确的事实。

（三）两种学习路径的效果分析。

在上述教学实践中，“圆的认识”的两种学习路径都能契合学生某方面的认知基础，均可顺利达成教学目标，并从不同侧面发展学生的素养。

路径一的优势在于以问题解决为方式和目标，容易调动学生的生活经验，激发学生的学习兴趣，具有较强的内在驱动力，学习过程注重实践操作，可以生成多种表象作为研究素材，活动形式丰富多样，生动、直观，能吸引更多学生参与；不足之处在于学生的认知容易停留在感知层面，不利于进一步抽象圆的要素和特征，并且，因为圆的作图方式不同于已知的平面图形（多边形），容易使其孤立于其他已知平面图形之外，会对后续的学习带来一定的障碍。

路径二的优势在于学习过程严谨，圆心、半径等要素贯穿于研究过程的始终，无须额外提取。同时，将圆与正多边形紧密联系在一起，通过类比和同化，使之纳入平面图形的体系之中。这一方面解释了学生心中关于方与圆两者之间关系的疑惑，另一方面为后续研究圆的周长、面积等内容提供了客观事实与思想方法的依据。但这一路径在初始阶段过于数学化，容易使部分学生望而生畏。若能在之前补充正多边形相关内容的学习，则更有利于学生形成研究思路。

实践表明，学生形成数学概念的基础、来源和方式是多角度、多渠道的，合理分析和利用历史相似性可以为教学提供不同的思路。在借助数学史料进行学习路径设计的过程中，不应随意实行“拿来主义”，而应充分了解并准确把握学生的认知基础和特点，在数学史料和学生认知之间找到契合点，使教学活动的设计有据可依，进而从不同角度丰富学生的认知途径。在选用不同的路径开展教学实践时，也不能贪多求全，而应有针对性地结合班级学生的已有水平和学习习惯加以选择，实现知识的逻辑顺序、知识的历史发展顺序和学生的认知发展顺序的一致性。当然，也可以在现有水平的基础上，尝试进行突破，将不同的学习路径进行整合，从整体的角度，兼顾数学学习的感性和理性两个层面。特别是在高年级的教学中，教师应当在考虑整体需求的基础上，进一步主动挖掘教学内容的历史依据和内在逻辑，尝试帮助学生进行更多的理性思考，促使学生的数学思维向更高的水平层次发展，以适应未来学习的需要。

参考文献：

[1]余庆纯，汪晓勤.中国HPM研究内容与方法[J].数学教育学报，2022，31（4）.

[2]曹培英.民族文化促进数学理解例谈：兼议HPM的实践探索[J].小学数学教师，2021（2）.

[3]摆超.数学史融入小学“圆”单元教学的课例研究[D].信阳：信阳师范学院，2022.

[4]张敏.从“以方测圆”到“化曲为直”：HPM取向的《圆的面积》教学[J].教育研究与评论（小学教育教学），2021（6）.

[5]李建良，岳增成.让数学概念在学生手中“复活”：HPM视角下“圆的认识”教学思考与实践[J].小学数学教师，2022（11）.

（作者单位：浙江杭州市萧山区夹灶小学） Y