建立相等关系，理解等号意义

【课前思考】

一、走近教材，体会编者意图

“挖红薯”这节课是北师大版（新世纪）小学数学第五版教材一年级上册第四单元“10以内数加与减”中一节新增加的内容，（如图1和图2）这是一节体会相等关系的内容。本节课在运用一一对应的方法比较数的大小、体会10以内数的加法与减法的意义的基础上，结合学生喜欢的“挖红薯”的生活情境，运用操作、画图等多种方法解决“妹妹想和哥哥的红薯一样多”的问题，直观地建立对等号表示相等关系的理解，丰富学生对等号意义及加、减法意义的理解。

本节课以解决“妹妹想和哥哥的红薯一样多”的问题为主线，设计了层层递进的3个问题。问题1是唤醒学生的学习经验，运用一一对应的方法比较谁的红薯多。问题2为开放性的问题，引导学生继续思考为了实现“一样多，你有什么办法”，引导学生发现妹妹再挖2个，就和哥哥挖的红薯的数量一样多，可以得到3＋2和5的数量是相等的，体会“=”是算式左右两边数量相等的数学表达。问题3在学生解决问题2的基础上，以“你能看懂吗”的方式呈现了淘气思考的过程，体现了等量关系的传递性，为学生感受数学运算背后的原理积累经验。同时，体会用数学算式表达实际问题的一般性和简洁性。

二、走近学生，寻找自主探索的生长点

在本课教学前对8名学生进行个体访谈，对80名学生进行课堂观察，其中，40名学生为北京市海淀区乡村学校学生，40名学生为成都市乡村学校学生。主要了解学生对理解一样多、建立相等关系是否存在困难，以及学生解决问题的思考过程和策略。

1.调研结果分析。

（1）比一比，谁挖的红薯多？

能够正确地回答哥哥挖的红薯多，妹妹挖的少，能清楚表达理由的学生达到100%。

（2）妹妹想和哥哥的红薯一样多，你有什么办法？

对80名学生进行课堂观察，发现学生均能用自己的方法解决问题。主要表现有以下三类：

表现1：添加的方法，即妹妹再挖几个红薯，使得妹妹的红薯和哥哥的红薯一样多。用此方法解决问题的学生有46名，占总人数的57.5%。

如，妹妹再挖2个就一样多了，3＋2＝5。（如图3）

表现2：移除的方法，即通过去掉哥哥挖的几个红薯，使得妹妹的红薯和哥哥的红薯一样多。能够想到用移除的方法解决问题的学生有24名，占总人数的30%。

如，哥哥拿走2个，剩下3个，5－2＝3，3＝3，一样多。（如图4）

表现3：重新分配。能够想到重新分配方法的学生有10名，占总人数的12.5%。

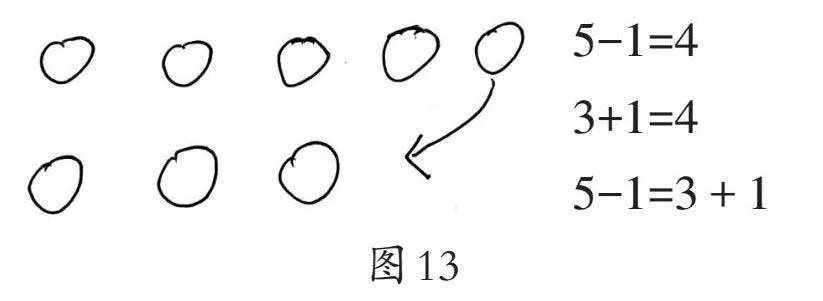
如，哥哥给妹妹1个，5－1＝4，3＋1＝4，妹妹的红薯和哥哥的红薯一样多。（如图5）

在同伴的交流、启发下，学生能够看懂并理解上述几种方法。

2.我的思考。

在调研前，我们一致认为，理解相等关系，对学生来说具有很大的挑战性。但从调研情况来看，添加、移除、重新分配在生活中经常用到，与儿童的真实生活联系紧密，为此，学生能结合已有的生活经验，通过摆圆片、画图等方法建立相等关系。这为我们的教学带来一定的启示：一是要基于学生的经验，给学生创造动手操作的机会，让他们直观体会、感悟相等关系；二是要鼓励学生探索和实践各种策略，使学生理解“=”所表示的相等关系的实际意义。

基于这样的思考，我们按照教材设计的“情境+问题串”，深入地开展探索活动，设定以下的学习目标：①结合具体情境，运用观察、操作、画图等方法进一步感受“=”的含义；②在探索怎样使两个数量“一样多”的活动中，逐步学会用数学语言交流、表达、解释或验证自己的想法。

【活动过程】

一、创设情境，提出问题

师：秋天到了，爷爷的小菜园丰收了。请大家仔细观察这幅图，（如图6）你发现了哪些数学信息？想到了哪些数学问题？

生1：哥哥和妹妹在挖红薯，哥哥挖了5个红薯，妹妹挖了3个。

生2：我想到的问题是，谁挖的红薯多？

生3：哥哥比妹妹多挖了几个红薯？

生4：妹妹比哥哥少挖了几个红薯？

生5：妹妹再挖几个红薯就和哥哥的一样多？

教师板书学生的问题。

师：同学们不仅能找到数学信息，还能根据信息提出数学问题。真棒！现在，我们来解决大家提出的数学问题。

二、自主探究，解决问题

1.解决问题1：比一比，谁挖的红薯多？

师：我们先来解决第一个问题：哥哥和妹妹，谁挖的红薯多？请同学们看下面的学习要求。

学习要求：①摆一摆或画一画，清楚地表达自己的思考过程。②和同伴说清楚谁的红薯多，以及你是怎么比较的。

教师带领学生理解学习要求，在学生明白学习要求的基础上，鼓励学生先独立思考，再同伴交流，教师巡视并及时解决学生遇到的困难。

师：谁来和大家说说你的想法？

生1：我用圆片代替红薯摆一摆，（如图7）哥哥挖了5个，妹妹挖了3个，哥哥的红薯多。

生2：我是用画图的方法，表示出哥哥挖的红薯多。（如图8）

师：通过摆一摆、画一画，大家用一一对应的方法，表示出哥哥挖了5个，妹妹挖了3个，我们可以清楚地看出哥哥挖的多，妹妹挖的少。

[教学思考]鼓励学生结合熟悉的情境，寻找数学信息并提出问题，并用一一对应的方法摆一摆或画一画，表达自己比较的过程和结果，一方面可唤醒学生原有的生活经验，另一方面从数学的角度进行表达，为解决后续问题埋下伏笔。

2.解决问题2：妹妹想和哥哥的红薯一样多，你有什么办法？解决问题3：你能看懂吗？

师：我们继续解决第二个问题，请大家看学习要求。

学习要求：①独立思考。②摆一摆、画一画，清楚地表达你的思考过程。③全班分享、交流。

教师带领大家理解学习要求后，学生自主思考，教师巡视并进行指导。

师：谁来和大家分享一下，你是怎么想的？请清楚地表达你的思考过程，倾听者要先安静地听，再补充或提问。

生1：我是用画图的方法，（如图9）妹妹再挖2个红薯，3＋2＝5，两个人都有了5个红薯，一样多。大家有问题或补充吗？

生2：我和你的想法一样，我也是让妹妹加上2个，这样妹妹也是5个，就一样多了。（如图10）

生3：我让哥哥拿走2个，5－2=3，哥哥有3个，3=3，和妹妹的一样多。大家还有补充吗？（如图11）

生4：哥哥去掉2个，也是3个，3=3，可以的。

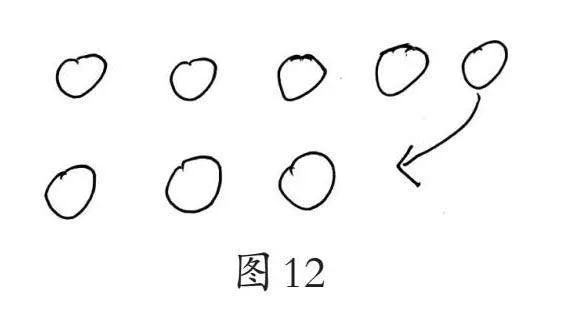
生5：我的方法和大家不一样，我是这样想的，哥哥给妹妹1个，5－1=4，哥哥有4个，妹妹添上1个，3＋1=4，妹妹也有4个。4=4，一样多了。（如图12）

生6：这种办法好有趣。我可以用算式记录。5-1=4，3+1=4，5－1=3＋1。大家能看懂吗？

师：请同学们仔细看看，能看懂他们的方法吗？这3个算式能表示一样多吗？（如图13）

生7：这种方法虽然有3个算式，但很容易看明白。从图中可以看到，哥哥比妹妹多了2个，给妹妹1个，哥哥就剩下4个，妹妹加上1个，也有4个，列算式是5-1=4，3+1=4。两个人都是4个，一样多，所以5-1=3+1。

师：用5-1=3+1表示，可以吗？

生：可以。5-1和3+1的得数是一样的。

师：我们用摆一摆、写一写、画一画的方式，探索出三种不同的方法。在讨论生5的方法时，我们还发现了5－1=3＋1，得到“＝”两边的数量是相等的，说明“＝”不仅可以表示结果，还能表示相等关系。老师为会思考、会观察、会表达的你们点赞。

[教学思考]在具象、可视化的学习活动中，鼓励学生探索怎样使两个数量“一样多”。在观察、操作、画图的过程中，运用添加、移走、重新分配这三种方法实现了妹妹和哥哥红薯数量同样多，进一步感受“＝”的含义。尤其是结合方法3，通过动手操作描述列出的算式，体会其中的变化过程，发现算式里的“＋”表示的是数量增加的变化，“－”表示的是数量减少的变化，“＝”的左边表示一个人的红薯数量，“＝”的右边表示另一个人的红薯数量，用“＝”连接起来，表示两个数量是相等的。在讲述现实世界里两个数量的故事中，体会等号不仅能表示运算的结果，也可以表示相等的关系，发展推理意识。

三、回顾反思，交流收获

师：这节课我们通过动手操作、画图解决了“妹妹想和哥哥的红薯一样多”的问题，你有哪些收获或感受？

生1：挖红薯的问题特别有趣。

生2：我发现了让两个数相等，有很多方法。

生3：我知道了“＝”以前表示一个得数（结果），现在它还表示两边是相等的。

生4：挖红薯的问题很有趣。我很喜欢第三种方法，他用画图和写算式的方法，每一步都很清楚，让我觉得很简单。

……

[教学思考]在回顾与交流中，一方面，肯定学生的自主探索；另一方面，在分享与交流中，梳理探索、解决问题的方法和策略，进一步丰富对“＝”意义的理解，再次明晰“＝”除了能表示结果，还能表示两部分的相等关系。

【课后思考】

在鼓励学生用摆一摆、写一写、画一画的方法，自主解决“妹妹想和哥哥的红薯一样多，你有什么办法”的问题时，我们欣喜地发现学生用了添加、移走、重新分配的方法，尤其是重新分配的方法，学生利用3个算式（如图13）清晰表达了推理过程。尽管这几个算式比较简单，但实际上展示了数学中的等量关系和等式的转换，算式“5-1=3+1”表示等式两边的数是相等的，体现了“=”的本质含义：等号的左边和右边是相等的。同时，体现了等式的传递性，即如果两个数都等于同一个数，则这两个数相等，用字母表示是：如果a=b且b=c，则a=c。这些对小学一年级的学生来说是难以理解的，不要求学生进行推理，只要学生了解背后的数学道理，体会、感知“=”的本质含义即可。

（作者单位：清华大学附属中学上地小学，作者系新世纪小学数学教材编写组成员） [WK]