目标贯通的数学复习课堂

【课例主题】

“师之蕴临港世外数学教师主题研修工作室”持续落实“数学课标植根课堂的课例研修”主题，本课例以“行程问题”的复习教学为例，探索数学复习课堂的有效方法。

【文本解读】

1. 课标衔接

方程在初等数学中占有较大比重，方程教学不仅是数学知识体系中的重要组成部分，更是培养学生逻辑思维和解决问题能力的重要途径。列方程解应用题不但在培养学生分析问题和解决问题的能力方面起到相当大的作用，而且还是解决实际问题的有力工具。课标要求学生能解一元一次方程，能根据现实情境理解方程的意义，能针对具体问题列出方程。在具体情境中，认识常见数量关系：路程=速度×时间，能利用这些关系解决简单的实际问题，能在较复杂的真实情境中，选择恰当的方法解决问题，形成运算能力和推理意识。

2. 单元素养

方程的建立与解法是锻炼学生逻辑思维能力的重要途径。数学中的方程，如同现实世界中的逻辑链条，每一步的推导都需要严谨的逻辑支撑。通过引导学生理解方程背后的数学逻辑，鼓励他们自主建立方程并探索其解法，旨在培养学生的思维条理性和严密性。这样的过程能够让学生在面对复杂问题时，保持清晰的头脑，有序地分析问题，提出合理的解决方案。方程单元教学也是提高学生计算能力的重要手段。在实际解题过程中，学生需要运用加减乘除、乘方开方等基础运算技能，以及代数式的变形、方程的求解等高级运算技巧。通过大量的练习和实践，学生能够逐渐提高运算速度和准确性，为将来的学习和生活打下坚实的基础。数学不仅仅是一门学科，更是一种工具，一种能够解决实际问题的工具。在方程单元的教学中，教师要引导学生将数学知识与现实生活相联系，学会用数学的眼光观察世界，用数学的方法解决问题。例如，在解决商品打折、利润计算等实际问题时，学生可以通过建立方程来找出问题的答案，从而感受到数学的魅力和价值。

3. 教材解读

“一次方程（组）和一次不等式（组）”这一教学单元，教材不仅教授了方程和不等式的解法，更重要的是，它蕴含了转化和类比的思想。这种思想在数学学习中至关重要，它能够帮助学生化繁为简，将未知转化为已知，将复杂问题简化为简单问题。类比思想也是这一单元的重要教学点。通过类比一次方程和一次不等式的解法，教师可以帮助学生更好地理解两者的联系和区别，提高解题的灵活性和准确性。教师不仅要让学生掌握方程和不等式的解法，更要让他们理解其中的数学思想和方法，培养他们的数学素养和思维能力。因此，在教学过程中，教师需要注重方程的应用，通过引入一些实际问题的例子，让学生将所学数学知识与实际问题相结合，从而更好地理解数学的应用价值。方程和不等式相关的实际问题，如购物问题、行程问题等，这些问题往往涉及多个变量和条件，需要学生运用所学的方程和不等式知识来求解。通过解决这些问题，学生不仅能够巩固所学的数学知识，更能够锻炼自己的数学思维和问题解决能力。

【学情分析】

本课授课对象是六年级2A班的学生，他们的思维活跃，但依赖性强，抽象概括能力相对较弱。本节课是对一元一次方程的应用进行的一次专题性的复习课，是学生在学习了一元一次方程及其解法的基础上进行的。班级大部分学生对方程的基本概念和运用较为熟悉，但在实际的计算中仍然存在部分问题。本节课旨在引导学生从行程问题中抽象出数学模型，建立方程并求解方程。教师以速度、时间及路程三者的关系为主线，从直线上的相遇和追及两种情形进行教学，通过学生思考、师生交流梳理行程问题的解题方法和步骤，充分给予学生反应以及自我生成整理的时间。在梳理方法的同时，让学生体会数学与实际生活的密切联系，渗透方程思想、数形结合思想，以激发学生学习数学的兴趣。

【课时目标】

1. 理解和掌握行程问题中的数量关系，并根据条件找准等量关系;2. 根据条件画出线段图并列出方程，解决实际问题;3. 在自主学习的过程中，经历行程问题的解答过程，体验数学知识与实际生活的密切联系，体会方程思想和数形结合的数学思想，培养解决问题的能力。

【课堂环节】

一、课前练习

1. 甲车的速度是每小时75千米，经过x小时行驶了____千米。2. 乙车3小时走了x千米，他的速度是千米/小时。3. 某一段路程x千米，如果乙车以45千米/小时的速度行驶，那么乙车行驶全程需要____小时。

复习：①行程问题中的三个基本量;②路程、速度、时间之间的关系;③三个量知二求一。

二、新知讲授

思考：1. 甲、乙两车分别从A、B两地同时出发，相向而行，两车会相遇吗？请画出线段图。

2. 如果两车相遇，则相遇时两车所走的路程与A、B两地的距离有什么关系？

例题1：甲、乙两车分别停靠在相距240千米的A、B两地，甲车每小时行50千米，乙车每小时行30千米。若两车同时相向而行，请问乙车行了多长时间后与甲车相遇？

变式：甲、乙两车分别停靠在相距240千米的A、B两地，甲车每小时行50千米，乙车每小时行30千米。若甲车先行1.6小时，两车相向而行，请问乙车行了多长时间后与甲车相遇？

题后小结：相遇问题的两种情况：①同时出发的相向而行;②一方先行，不同时出发的相向而行。

思考：3. 甲、乙两车同一地点同向而行，乙车先出发a小时甲车再出发，在什么情况下两车能相遇？4.如果甲车能追上乙车，你能画出线段图吗？

例题2：甲、乙从同一点出发，同向而行，甲每小时走3km，乙每小时走2km，乙先出发3小时，甲再出发追赶乙，问甲要多久才能追上乙？

变式1：A、B两地相距4km，甲、乙两人分别从A、B两地同时同向出发去往C地（B地离C地更近），甲每小时走3km，乙每小时走2km，问甲要多久才能追上乙？

变式2：已知A、B两地相距240km，甲、乙两人分别从A、B两地出发，甲的速度为40km/h，乙的速度为20km/h。（1）若甲乙同时相向行驶，几小时后两人相距60km？（2）若甲乙同时同向行驶（甲在乙后），几小时后两人相距60km？

题后小结：追及问题的两种情况：①同时不同地;②同地不同时。

说明：这一环节是为教学目标2、3服务。

三、当堂检测

练习：甲、乙两车分别从相距120km的 两地出发，甲车速度为70km/h，乙车速度为50km/h。（1）两车同时出发，相向而行，经过____小时两车相遇。（2）两车同时出发，同向而行（乙车在前甲车在后），经过____小时甲车追上乙车。（3）两车同时出发，相向而行，多长时间后两车相距60km？

四、课堂小结

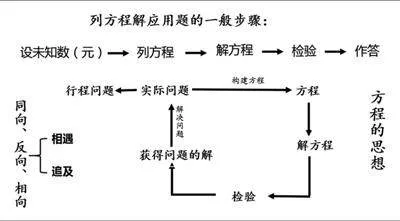
1. 列方程解应用题的一般步骤。2. 行程问题的三个基本量。3. 行程问题的两种题型。4. 行程问题的分析方法。

五、作业布置

1. 梳理学习单。2. 完成课后作业单。

六、板书设计

七、课后作业单

1. 请列方程完成以下题目：以下是两张不同类型（“Dxxx次”表示动车，“Gxxx次”表示高铁）的车票：（1）根据车票中的信息填空：该列动车和高铁是______（填“相”或“同”）向而行，该列动车比高铁发车______（填“早”或“晚”）。（2）已知该列动车和高铁的平均速度分别为200km/h、300km/h，两列列车的长度不计，高铁比动车早到1h，求A，B两地之间的距离。

2. 甲、乙两地相距72km，一辆工程车和一辆洒水车上午6时同时从甲地出发，分别以v1km/h、v2km/h的速度匀速驶往乙地。工程车到达乙地后停留了2h，沿原路以原速返回，中午12时到达甲地，此时洒水车也恰好到达乙地。（1）v1=______，v2=______;（2）出发______小时后，两车相遇？（3）求出发多长时间后，两车相距30km？（列方程解）

3. 问题情境：在高铁站上车的小明发现：坐在匀速行驶动车上经过一座大桥时，他从刚上桥到离桥共需要150秒;而从动车车尾上桥开始到车头离桥结束，整列动车完全在桥上的时间是148秒。已知该列动车长为120米，求动车经过的这座大桥的长度。

合作探究：

（1）请补全下列探究过程：小明的思路是设这座大桥的长度为x米，则车头上桥开始到车尾离桥的长度为（x+120）米，所以动车的平均速度可表示为____米/秒;从动车车尾上桥开始到车头离桥结束的路程为（x-120）米，所以动车的平均速度还可以表示为____米/秒。再根据火车的平均速度不变，可列方程____________。

（2）小颖认为：也可以设动车的平均速度为v米/秒，列出方程解决问题。请你按照小颖的思路求动车经过的这座大桥的长度。

【执教反思】

本节课旨在探索数学复习课堂的有效路径与方法。在教授本课之前，教师对教案经过反复设计与修改。在正式教学中，通过课堂实践，对数学复习课堂的教学有了更多的领悟，对如何在复习课堂中落实教学目标也有了新的认识。

一、列表和画线段图解题是数学复习课堂教学精彩所在

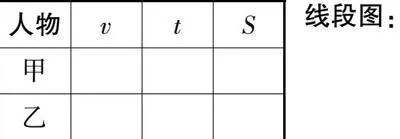
本课例主要探索“数学复习的教学课堂”的教学方法，在数学复习课堂上，画线段图与列表分析等量关系这两种解题技巧尤为关键，它们不仅能够帮助学生理清各个关键量之间的关系，为设出未知数并列出方程提供有力的支持。

在解决行程问题的课堂上，本课充分发挥了列表与画线段图的优势，通过引导学生分析题目中的关键信息，学生能够准确地列出表格并画出线段图，继而求解行程问题。

二、灵活学与教，促进师生课堂更加有效互动

在本课教学中，虽然教师一直坚持教学生如何思考、如何分析问题、如何解题，但在授课中过于依赖讲解和自我演示，引导较多，导致学生只能按教师框定的方式去思考问题。这种教学方式虽然能够帮助学生掌握一定的解题方法与策略，却限制了学生的思维发展，少数学生并不能正确画出线段图从而找到各个量之间的关系，也无法激发他们的学习兴趣。在以后授课过程中，教师应更加注重学生的主体地位，鼓励学生自主思考，自主探究。当学生在分析问题的过程中遇到困难时，应及时给予指导，帮助学生找到问题的症结所在，避免学生因挫败感而失去学习动力。

三、例题的难度适当加深会更加符合复习课的要求

在数学复习课上，例题难度的适当提高符合复习课要求的策略深化。复习课不是对已学知识的简单重复，而是要在巩固基础知识的基础上适当提高和拓展。本节课教学过程中的例题过于侧重基本知识与方法的复习，而忽略了复习课的适当提高，没有给予学生足够的探索空间，作为复习课型可以在教学过程中适当加入有思维量的题型，通过解答这些有思维量的题型，帮助学生更好地巩固已学知识，拓展自己的思维能力和创新能力，激发学生的探索欲和求知欲。

总之，行程问题作为一元一次方程学习过程中的一个重要应用场景，其重要性不言而喻。这一领域的问题，不仅考查学生对一元一次方程知识的掌握程度，更检验他们如何将理论知识应用于实际情境，以及如何通过逻辑思维和数学工具解决复杂问题的能力。在数学教育中，教师应该充分重视行程问题的教学，并通过多种方式帮助学生掌握其解决方法和思维过程。

（责任编辑：淳 洁）