基于数学建模方法的矿石加工质量预测研究

摘要：本文基于数学建模方法对矿石加工质量指标进行了预测研究。应用两个Excel附件数据表，将数据分为三种情形，运用五类模型（线性回归、随机森林、决策树、XGBoost、GBDT模型）对相关数据进行了不同维度的数据预测.为了得到模型的拟合精度，应用了决策系数法对五类模型的预测效果进行了定量分析，最终选择决策树与GBDT模型分别对矿石加工质量指标与矿石加工合格率进行了预测研究.本研究通过实验验证了所提出模型的有效性和可行性，对于提升工业生产效率和产品质量具有一定的实际应用价值。

关键词：矿石加工；质量与合格率；决策树； GBDT算法

中图分类号：O29 文献标志码：A 文章编号：1001-2443（2024）05-0401-06

引言

随着矿产资源的逐渐枯竭和对高品质矿石需求的不断增长，矿石加工质量控制成为矿业领域亟需解决的重要问题之一。矿石的质量直接关系到后续冶炼和生产的效益，因此对矿石加工质量进行准确预测和控制显得尤为迫切。

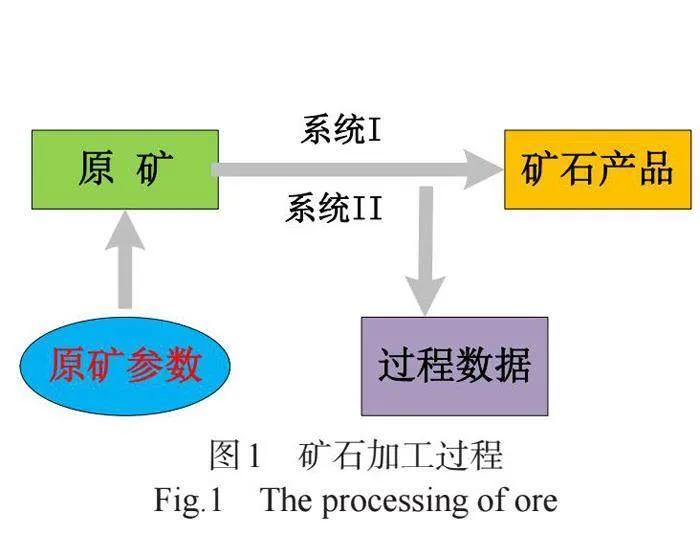
一般地，矿石加工质量控制流程如图1所示。矿石加工质量控制的传统方法主要依赖于经验和试验，这种方法在效率和准确性上存在一定的局限性［1］。随着数学建模技术与新方法的涌现，其在解决实际问题中的应用，逐渐受到各个领域的重视［2］。本研究旨在利用数学建模方法，通过对矿石样本的大量数据进行分析和挖掘，建立一个高效、精确的矿石加工质量预测模型。

在矿石加工质量预测中，我们采用线性回归模型、随机森林模型、决策树模型、XGBoost模型［3］以及GBDT模型，结合大量的实验数据，建立一个多维度、不同影响因素的矿石加工质量控制模型。通过该模型，我们能够更全面、更准确地了解矿石的特性与质量，并提前预测加工后的质量与矿石加工的合格率，从而可以更好地改进与提高矿石加工工艺与相关流程等，以期为矿业领域的矿石加工质量控制提供新的评价方法。

通过本研究，我们期望能够为矿石加工行业提供一种基于数学建模方法的质量控制手段，促进矿产资源的可持续利用和矿业生产的智能化发展。

1 数据来源与预处理

本文研究的两个附件1与附件2的Excel数据来源于“2022年第十九届五一数学建模竞赛”题中的B题。其中附件1中有三个数表，第一个是系统温度（包含系统I温度和系统II温度），第二个是产品质量（包含四列数据，分别是质量指标A、B、C、D），第三个是原矿参数（包含四列数据，分别为原矿参数1、2、3、4）。附件2中的数据包含四个Excel数据表，分别是系统温度、产品质量、原矿参数、过程数据。根据研究的需要，我们应用python的pandas库中的concat、merge、groupby等函数将附件1与2中的数据进行了相应的合并处理与backfill填充。

2 方法与模型

2.1 决策系数

我们知道，对数据进行预测的方法和数学模型有很多，例如回归模型、灰色模型、神经网络模型、时间序列模型等［4］。我们也知道不同模型对数据的预测能力并不相同，究竟选择哪一种模型来做数据的预测更合理、更准确呢？注意到，对数据进行预测，其评估预测精度与拟合度的函数，即决策系数公式R2，它能评估预测数据与真实数据之间的匹配程度，以此来帮助我们选择最佳的预测模型，R2的数学公式如下：

[R2=1-i=1n（yi-yi）2i=1n（yi-y）2=1-RSSi=1n（yi-y）2]，

其中[yi]表示数据真实值，[yi]表示数据的预测值，[y]表示数据的样本均值；R2表示预测的数据与真实值的拟合度，其值介于0到1之间，若值越接近1，则表示模型所解释的实际值越多，即说明该模型的解释性能越好; RSS表示数据的残差平方和［5］。

2.2 决策树模型原理

决策树模型简单直观、易于理解和解释，适用于离散型和连续型特征，对异常值和缺失数据具有较好的鲁棒性［6］。决策树由节点和边组成，其中节点表示特征或属性，边表示特征的取值。根节点代表最重要的特征，分支节点代表中间特征，叶节点代表最终的分类或回归结果。决策树的构建包括特征选择、节点分裂和停止条件。决策树模型的最佳特征作为当前节点的判别标准，常用的方法包括信息增益、信息增益率、基尼系数等。该模型在节点分裂时，算法将数据集选定的特征进行划分，生成子节点。在达到预定条件时停止分裂，其停止的条件可以是树的深度达到一定值、节点中的样本数小于阈值等。决策树模型的核心思想是，在做预测问题时，其算法是将输入特征映射到数值输出，即叶节点就包含预测的数据。

2.3 GBDT原理与算法

梯度提升决策树（Gradient Boosting Decision Tree，即GBDT），是一种迭代的决策树算法［7］，它通过构造一组弱的学习树，并把多棵树的结果累加作为最终的预测输出。该算法将决策树与集成思想进行了有效结合。也就是将梯度提升树和CART回归树结合起来，其主要思想是每一轮迭代使用一个新的CART回归树来拟合上一轮模型预测值与真实值的残差。具体来说，是用损失函数的负梯度作为残差近似值，每轮的CART回归树拟合这个残差近似值。

在GBDT算法的迭代中，假设前一轮迭代得到的强学习器是[ft-1（x）]，损失函数是[L（y，ft-1（x））]。迭代的目标是找到一个CART回归树模型的弱学习器[ht（x）]，让本轮的损失：

[L（y，ft（x））=L（y，ft-1（x）+ht（x））]

达到最小。也就是说，本轮迭代找到一个CART回归树，使本轮损失变得更小。由于GBDT选择了平方损失，则损失函数可化简为：

[L（y，ft-1（x）+ht（x））=（y-ft-1（x）-ht（x））2 =（r-ht（x））2，]

其中[r=y-ft-1（x）]，是当前模型拟合数据的残差。而GDBT算法每轮生成的CART回归树就是要拟合这个残差。GBDT算法的一般步骤如下：

（1）初始化[f0（x）=0]；

（2）对[m=1，2，…，M]及样本序列数[i=1，2，…N]，计算残差

[rmi=yi-fm-1（x）， i=1，2，…N]；

（3）拟合残差[rmi]中的强学习器[fm（x）]，其更新如下

[fm（x）=fm-1+hm（x）] ；

（4）循环重复上面两步算法，直到损失函数值小于阈值时停止，得到梯度提升树，即[fM（x）=m=1Mhm（x）]。

3 结果及其分析

3.1 矿石加工质量的预测结果及其分析

数据表中的附件1有三个Excel数据表，其中温度数据（系统I温度与系统II温度）是每隔一分钟采样一次温度数据，每天有1439个温度数据值；矿石加工质量指标数据是每隔一小时采样一次数据值，一天有24个指标数据值；原矿参数是每天采样一次数据值，即一天一个数据值。根据已有数据的特征，我们选取了2022年1月13日至2022年1月22日共计十天的数据来做矿石加工质量预测。在给定的2022-01-23原矿参数（附件1）和系统设定温度（如表1所示，假设系统温度与调温指令设定的温度相同）下，其目标是给出矿石加工产品质量指标的预测结果。

由于在所给数据中，存在不确定因素的影响，在相同（或相近）的系统温度下生产出来的矿石产品质量可能有较大的差别，且三个数据表的维度不一样，因此，我们分三种情形来预测矿石加工质量指标，然后取这三种情形下的平均值作为最终矿石质量指标的预测值。

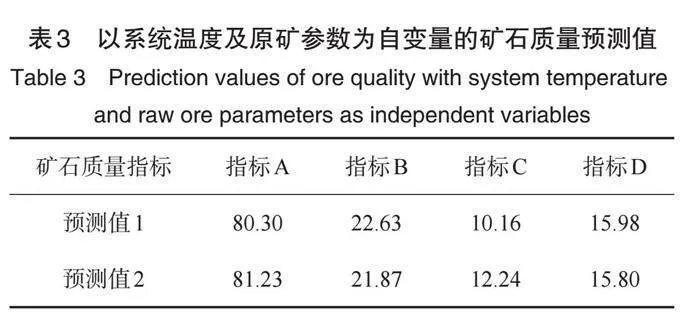
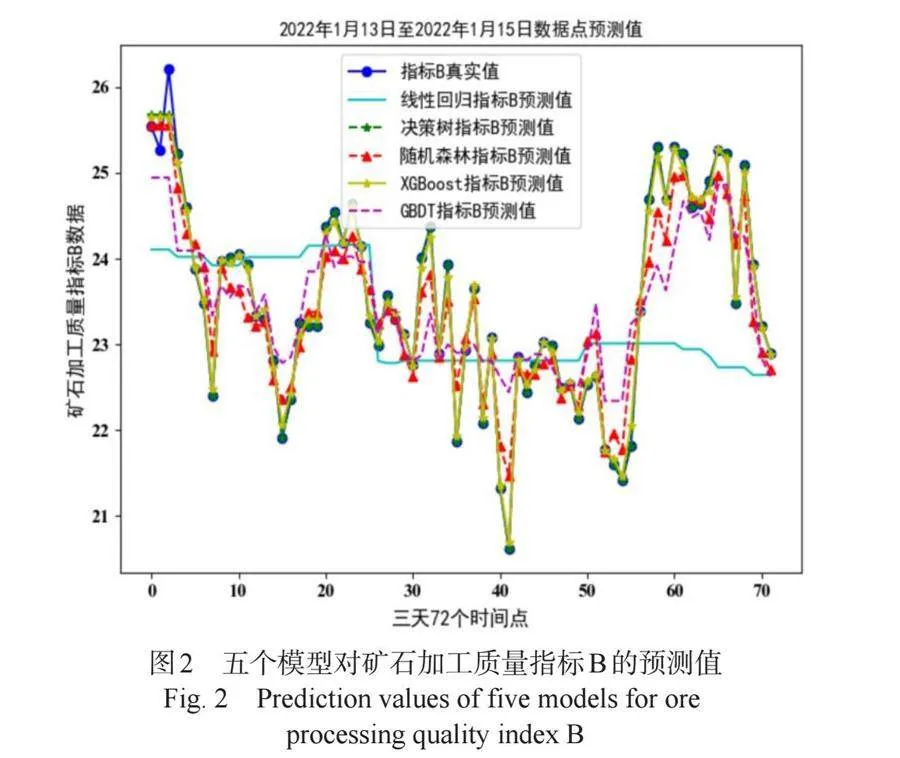
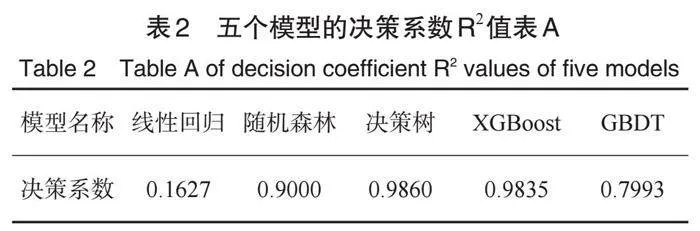
情形1：基于系统I与系统II温度、原矿参数为模型输入变量（即自变量），以矿石加工质量指标A、B、C、D的每天一小时采样数据（共计十天），一共240行数据，然后进行数据合并处理，其中，温度数据以矿石质量指标时间点进行采样获取，而原矿参数的空缺值则以fillback填充方式补齐。我们分别以矿石质量指标A、B、C、D的数据作为模型因变量（被解释变量）。基于自变量和因变量数据，对五个模型（线性模型、随机森林、决策树、XGBoost、GBDT）进行训练，以矿石质量指标B为例，我们给出了真实值与预测值的对比图（部分展示），如图2所示。从该图可看出，不同的模型，其预测的数据值有显著差距。表2中以系统I温度、系统II温度以及原矿参数为自变量，而以矿石质量指标B为因变量训练五个模型得到的模型预测拟合度，即模型的决策系数值。从表2中看出，决策树模型的拟合度最好，其值为0.9860，而线性回归模型的拟合度最差，其值为0.1627。 因此，我们采用决策树模型并训练之后再来预测矿石加工质量指标值。其中，以表1中设定温度值以及原矿参数为自变量，应用决策树模型预测得到的矿石质量指标，结果如表3所示。 把预测结果与以往数据对比可知，其预测效果理想。

情形2：按照每天系统I温度与系统II温度每隔一分钟观测到的14229个样本值以天（共10天）为单位的平均值温度（十行数据）为模型自变量，而以矿石加工质量指标B的数据为模型的因变量，以此来训练模型，得到了相应模型对矿石质量指标B的预测值，方便起见，我们给出了数据，如图3所示。

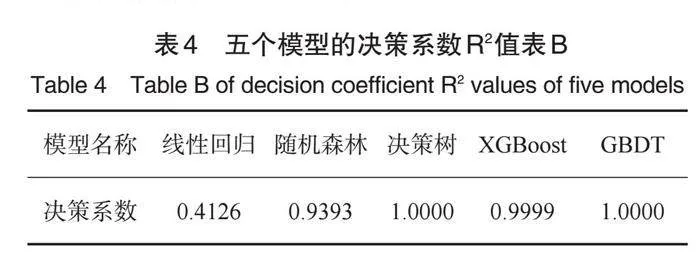
这五个模型的预测值与真实值具有一定的差距。为了看出它们对数据的预测精度，我们给出了这五个模型的决策系数值，如表4所示。从表4看出，其决策树和GBDT模型的预测精度最好，达到了完全拟合的程度，其值为1，拟合最差的为线性回归模型，其拟合精度只有0.4126。因此，我们基于表1中的指定两个系统温度值，应用决策树模型预测矿石加工质量指标，其结果如表5所示。其预测结果数据对比以往相应数据可知，其预测效果是理想的。

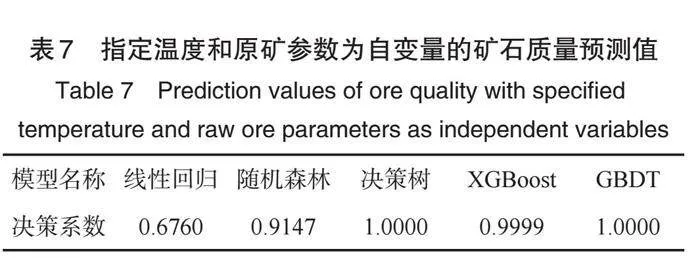
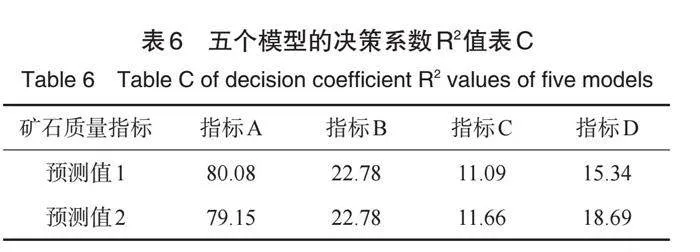
情形3：在情形2的基础上，将模型的自变量修改为系统I与II的温度及矿石参数为五个模型的输入自变量，而以矿石加工质量指标B数据为模型因变量进行模型训练。由训练后的模型，我们得到矿石质量指标B的预测值，其结果如图4所示，从该图可看出，决策树、XGBoost与GBDT模型所得到的预测值几乎重合。与此同时，我们还给出了模型的拟合精度值，见表6所示，其中拟合精度达到1的有决策树和GBDT模型。基于表1中指定系统温度值，我们应用决策树模型得到了矿石质量预测值，如表7所示，其预测效果良好。

在上述三种情形下，我们分别得到了在指定系统I和系统II温度（表1所示）及其它因素影响下的矿石加工质量预测值.基于表3、5、7，我们求其预测值的平均值得到了矿石质量指标的最终预测值，如表8所示。

4.2 矿石加工质量合格率预测结果及其分析

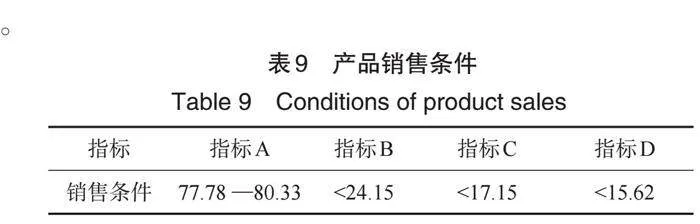
过程数据是在矿石加工过程中检测得到的（见图1），可以反映原矿质量.由于同一批次（天）的原矿质量有差别，也可能造成在传入相同或相近调温指令后生产出来的产品质量有差别。附件2的数据给出了该生产车间2022-01-25至2022-04-07的生产加工数据及过程数据.其中表9给出了矿石产品的销售条件，满足销售条件的产品视为合格产品，否则视为不合格产品。

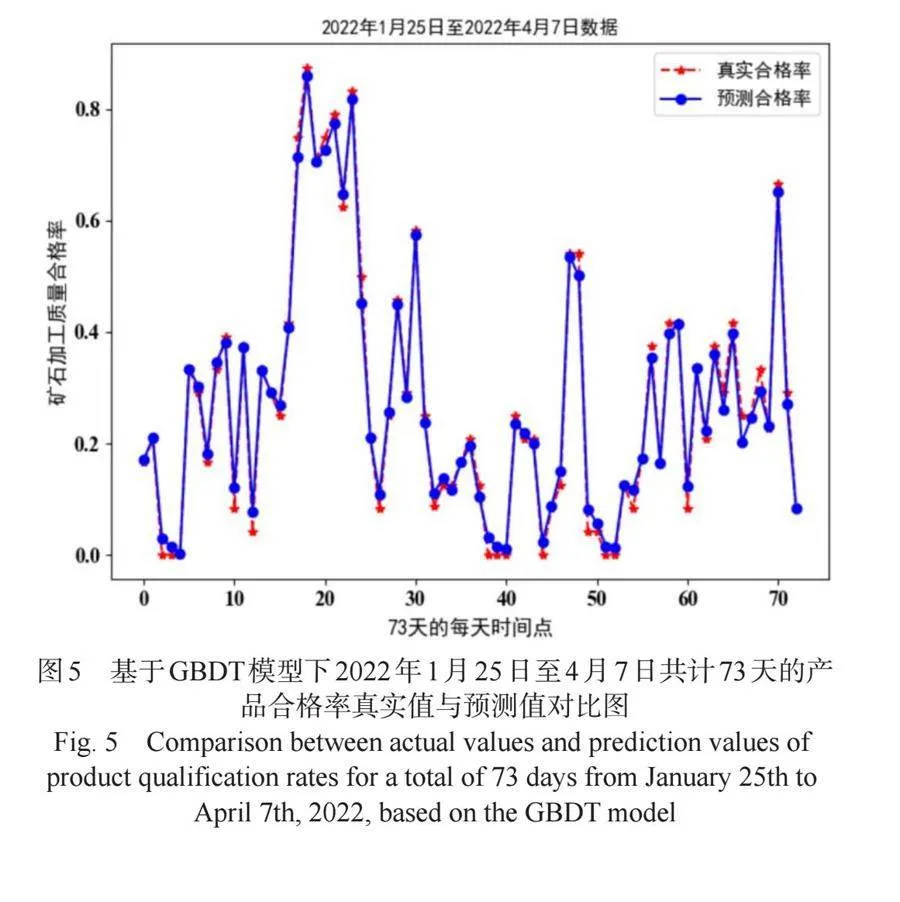
我们对数据表附件2中的数据进行预处理，即选取系统I温度、系统II温度、原矿参数1至4和过程参数1至4作为GBDT模型输入的自变量，而以矿石加工质量合格率（合格率的计算公式为：合格率=合格产品数/产品总数）作为模型因变量进行模型训练，以此得到了矿石产品合格率的真实值与预测值的对比图5。从图5可看出，基于GBDT模型预测的数据和真实值之间的差距非常小，其拟合精度的决策系数为0.9919，其预测效果优良。

我们基于训练好的GBDT模型来预测矿石产品合格率。在给定的时间2022-04-08与2022-04-09的原矿参数、过程数据（附件2中的数据）和系统设定温度，即表10的第2列和第3列所示，我们应用GBDT模型预测矿石加工质量的合格率分别为0.4815与0.2375，如表10的第4列所示。根据预测值来看，给定两个系统的设定温度下，其矿石加工质量的合格率并不高.这说明选择好的矿石原料是矿石加工质量的保证，而加工方法与工艺技术的改进是提高矿石加工合格率的直接有效的手段。

5 结语

本文通过五个数学模型（线性回归、随机森林、决策树、XGBoost、GBDT模型）以及决策系数方法研究了矿石加工质量指标的预测值与合格率问题。通过决策系数对模型的拟合精度大小，我们选择了决策树模型研究了基于给定系统温度下的矿石加工质量指标的预测值，以及应用GBDT模型对给定系统温度下的矿石加工合格率进行了预测。本文应用的预测方法与所得结果，对实际应用具有一定的参考价值。

参考文献：

［1］ 李大潜. 现实世界的数学模型是数学的研究对象——介绍高尔斯《数学》［J］. 数学建模及其应用，2023，12（1）： 107-109.

［2］ FARID A， MARAT A， JOSHUA Z， KAMIL K， NAILYA S， WU D. On quantum methods for machine learning problems part I： quantum tools［J］. Big Data Mining and Analytics， 2020， 3： 41-45.

［3］ XIAO M， YIN M M， DING H， GENG X F， SHEN Y J， CHEN L Q. Modeling， analysis， and simulation of X-shape quasi-zero-stiffness-roller vibration isolators［J］. Applied Mathematics and Mechanics， 2022， 43（7）： 1027-1044.

［4］ 刘 班. 数据挖掘及其Python 实现技术研究［J］. 信息通信， 2020， 9（213）： 63-65.

［5］ 于晓虹， 徐海燕， 楼文高. 人口预测的投影寻踪自回归模型构建与实证［J］. 统计与决策， 2022， 23（611）： 38-41.

［6］ 陈春梅， 王正元， 屈娜. 人工智能优化算法综述［J］. 大学， 2020， 26：71-72.

［7］ 刘向丽， 崔文泓. 一种基于决策树的用于构建量化策略的分类器［J］. 纯粹数学与应用数学， 2023， 39（3）： 339-349.

Research on Quality Prediction of Ore Processing Based on Mathematical Modeling Methods

ZHOU Xiang-hui， XU Kai

（School of Mathematics and Statistics， Anhui Normal University， Wuhu 241002，China）

Abstract： A prediction problem on the quality indicators of ore processing is studied by mathematical modeling methods. Two data tables of Excel attachment are used to divide the data into three types. Five models （linear regression， random forest， decision tree， XGBoost， GBDT model） are used to predict the relevant data from different dimensions. In order to obtain the fitting accuracy of the model， the method of decision coefficient is applied to quantitatively analyze the prediction effect of the five models. Naturally， the decision tree and GBDT models are selected to predict the quality indicators of ore processing and the qualification rate of ore processing， respectively. This study verifies the effectiveness and feasibility of the proposed models via experiments， which has certain practical application value for improving industrial production efficiency and product quality.

Key words： ore processing; quality and qualification rate; decision tree; GBDT algorithm

（责任编辑：马乃玉）