融合混沌映射和自适应T分布的蜣螂优化算法

摘要：针对原始蜣螂优化算法（DBO）存在的收敛精度低、易陷入局部最优等问题，提出一种改进的蜣螂优化算法。该算法采用混沌映射初始化蜣螂种群以提高种群的多样性，引入北方苍鹰优化算法的勘探策略以增强算法的全局勘探能力，并改进一种非线性边界收敛因子以平衡其收敛速度和收敛精度。同时，采用自适应T分布扰动策略以增强算法跳出局部最优的能力。实验结果表明，改进后的DBO算法在15个基准测试函数的求解寻优中，有13个测试函数的求解结果优于原始蜣螂优化算法、麻雀搜索算法、灰狼优化算法、鲸鱼优化算法和哈里斯鹰优化算法的求解结果，表现出更高的收敛精度、更快的收敛速度及更高的稳定性。

关键词：蜣螂优化算法；混沌映射；T分布扰动；基准测试函数

中图分类号：TP181文献标志码：A

0引言（Introduction）

蜣螂优化算法［1］是由东华大学的沈波教授及其团队于2022年提出的一种新型智能优化算法，该算法目前已广泛应用于无人机路径规划［2］、无线传感器网络的节点部署［3］以及故障诊断［4］等领域。然而，DBO算法仍存在收敛精度低、易陷入局部最优等问题。针对这些问题，已有不少学者对其进行了改进研究。例如，LI等［5］提出了一种自适应步长策略和随机差分变异策略相结合的蜣螂优化算法，增强了算法跳出局部最优的能力；郭琴等［6］提出了一种融合麻雀搜索算法追随机制的扰动策略和柯西高斯变异的蜣螂优化算法，提高了算法的收敛速度和收敛精度；ZHU等［7］提出了一种基于量子计算和佳点集初始化的蜣螂优化算法，进一步优化了算法性能。

针对蜣螂优化算法存在的问题，本文提出了改进的蜣螂优化算法IDBO。该算法通过在种群初始化时引入piecewise映射，显著提升了种群的多样性。同时，通过引入北方苍鹰优化算法的勘探策略，提高了本算法的全局搜索能力。为了进一步优化性能，本算法中设置了非线性边界收敛因子，平衡了算法的收敛速度和收敛精度。此外，通过引入自适应T分布扰动，进一步提高了算法跳出局部最优的能力。实验结果显示，在15个基准测试函数的求解寻优中，本算法相较于其他算法，普遍表现出更为优越的性能。

1蜣螂优化算法（DungBeetleOptimizationalgorithm）

蜣螂优化算法是从自然界中蜣螂的5种特定行为——滚球、跳舞、繁殖、觅食和偷窃中汲取灵感而设计的一种智能优化算法。

1.1滚球行为

当在滚球的过程中没有遇到障碍，蜣螂会利用天体进行导航，此时其位置更新公式如下：

xt+1i=xtiy1K6OcGAYVNdje1JD5vecw==+α·k·xt-1i+b·〖JB（|〗xti-xtworst〖JB）|〗[JZ）][JY]（1）

其中：t为当前迭代次数；xti表示第i只蜣螂在第t次迭代时的位置；α是值为-1或1的自然系数；k是（0，0.2）之间的常数，称为偏转系数；b是（0，1）之间的常数；〖JB（|〗xti-xtworst〖JB）|〗为周围环境的变化，其中xtworst表示当前种群中最差的蜣螂位置。

1.2跳舞行为

当在滚球的过程中遇到障碍，蜣螂会通过跳舞的方式重新确定滚球方向，而跳舞行为则是通过切线函数完成的，滚球方向θ在（0，π）之间，当滚球方向重新确定后，蜣螂将继续滚动粪球，此时其位置更新公式如下：

1.3繁殖行为

合适的产卵地点对于蜣螂繁育后代十分重要，因此蜣螂会将粪球滚到安全且适合产卵的区域，并进行隐藏。根据蜣螂的这种行为，给出一种边界选择策略（3）用于模拟繁殖蜣螂的产卵区域：

其中：Lb*和Ub*分别表示产卵区域的下限和上限，xtlbest为当前局部最佳位置，R=1-t/T为线性收敛因子，T为最大迭代次数，Lb和Ub分别为要优化问题的下限和上限。

当产卵区域确定后，繁殖蜣螂就会开始产卵，并且每次迭代只产出一枚卵，由公式（3）可知，产卵区域是动态变化的，因此卵的位置也是动态更新的。此时，其位置更新公式如下：

其中：Bti为第i个卵第t次迭代时的位置，[WTHX]b[WTBX]1和[WTHX]b[WTBX]2为1×D的独立随机向量，D表示优化问题的维度。

1.4觅食行为

当幼虫破卵而出并成长为小蜣螂后，通常会出来觅食，根据公式（5）对其觅食区域进行限定：

其中：Lbl和Ubl为小蜣螂觅食范围的下限和上限，xtgbest为当前全局最优位置，其位置更新公式如下：

1.5偷窃行为

在蜣螂种群中存在偷窃粪球的行为，其位置更新公式如下：

xt+1i=xtgbest+S·[WTHX]g[WTBX]·（|xti-xtlbest|+|xti-xtgbest|）[JZ）][JY]（7）

其中：S为常数，[WTHX]g[WTBX]为服从正态分布的随机向量。

在种群中，滚球蜣螂、繁殖蜣螂、觅食蜣螂和偷窃蜣螂的比例为6∶6∶7∶11。

根据“天下没有免费的午餐”这一普遍原理，蜣螂优化算法与其他智能优化算法一样，都存在全局搜索与局部开发之间的不平衡、收敛精度差及易陷入局部最优的问题。为克服这些缺陷，本研究提出一种改进的蜣螂优化算法，旨在通过一系列创新策略对原有算法进行修正与优化。

2.1混沌映射

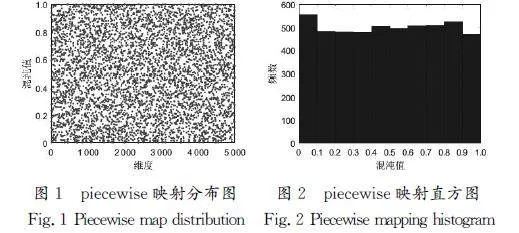
由于种群初始化是随机的，所以容易出现种群分布不均匀的情况，导致种群的多样性下降，进而对后续的寻优造成影响。考虑到混沌映射具有随机性和混沌遍历性的特性，因此常被用来代替随机数发生器，以增加种群的多样性。本文引入piecewise映射优化种群初始化过程，如图1和图2所示分别为piecewise映射分布图和piecewise映射直方图。

2.2引入北方苍鹰优化算法的勘测策略

在滚球蜣螂无障碍前进阶段引入北方苍鹰优化算法［8］的勘探策略。由于在原始蜣螂优化算法中滚球蜣螂更新策略涉及的参数较多，并且各蜣螂之间相互孤立，不存在信息交流，这会导致优化算法过早收敛并陷入局部最优而无法找到全局最优解。北方苍鹰优化算法在勘探阶段对猎物的选择是随机的，即任意选定一个粪球并进行滚动，因此能够克服原始蜣螂优化算法存在的缺点，增强算法全局寻优的能力；无障碍前进阶段滚球蜣螂位置更新公式为

其中：xt+1i为第i只滚球蜣螂第t+1次迭代的新位置，xti为第i只滚球蜣螂第t次迭代的原位置，pi为第i只滚球蜣螂选择的粪球的位置，r是［0，1］之间的随机数，I为1或者2的整数，Fi为第i只滚球蜣螂位置的目标函数值，FPi为第i只滚球蜣螂选择的粪球位置的目标函数值。

2.3非线性收敛因子

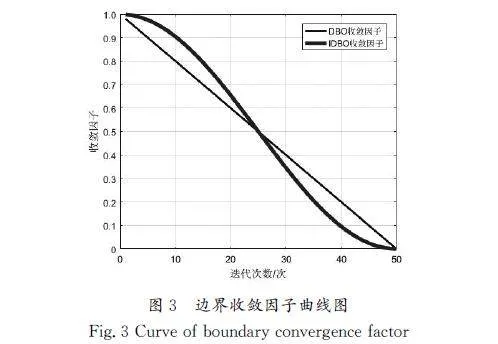
由原始蜣螂算法可知，蜣螂的繁殖和觅食行为被规定在一个动态变化的范围内，其中线性收敛因子R=1-t/T，它虽然会随着迭代次数的变化而动态更新，但是依然难以表征在真实的自然界中蜣螂繁殖和觅食的复杂性。此外，在迭代的前期，通常研究人员希望算法能够对全局可行区域进行更为广泛的搜索，而在迭代后期更加注重在最优解附近的局部开发，以加快其收敛速度。因此，提出一种余弦收敛因子重新对其范围进行规定，公式为

DBO算法和IDBO算法的边界收敛因子曲线图如图3所示，由此可知，改进后的DBO算法边界收敛因子在迭代的前期以一个较慢的速度下降，扩大了蜣螂繁殖和觅食的范围，提高了算法的全局探索能力，而在迭代的后期以一个较快的速度下降，加快了算法的收敛速度。

2.4引入自适应T分布扰动

为了进一步增强蜣螂优化算法在全局探索与局部开发之间的平衡能力，本文研究在小蜣螂觅食阶段引入自适应T分布干扰。t（iter）为以迭代次数iter为自由度参数的T分布变异扰动，使用其对小蜣螂的觅食行为进行扰动。在迭代的开始阶段，T分布扰动与柯西变异类似，这使得蜣螂算法在此时具有较强的全局探索能力；而在迭代后期，T分布扰动类似于高斯变异，此时算法的局部开发能力更为突出，同时算法的收敛速度也得以提升，新位置的更新方式如公式（10）所示：

2.5改进后的算法流程

步骤1：使用piecewise映射初始化蜣螂种群，增加种群多样性。

步骤2：计算蜣螂种群的适应度值，更新当前最优位置。

步骤3：蜣螂在滚球无障碍前进阶段使用公式（8）更新蜣螂位置，在滚球过程中遇到障碍时，使用公式（2）更新蜣螂位置。

步骤4：对于繁殖蜣螂和觅食蜣螂分别使用公式（4）和公式（10）更新蜣螂位置。

步骤5：对于偷窃蜣螂使用公式（7）更新蜣螂位置。

步骤6：对每只蜣螂进行边界判定，更新计算当前适应度值及最优值。

步骤7：判定t是否为最大迭代次数，若是，则停止更新；反之，返回“步骤3”继续执行。

3基准测试函数（Benchmarktestfunction）

3.1实验设置

本文选取CEC2005基准测试函数中的15个函数进行性能测试，其中F1～F7为单峰测试函数，其有且只有一个最优解，可以使用其对算法的局部开发性能进行检验；F8～F13为多峰测试函数，与单峰测试函数不同，多峰测试函数除了有一个全局最优解，还存在多个局部最优解。此时，大多算法往往会陷入局部最优而无法找到全局最优解，因此可以用来测试算法的全局探索能力；F14、F15为固定多峰测试函数。基准测试函数如表1所示。

3.2实验结果

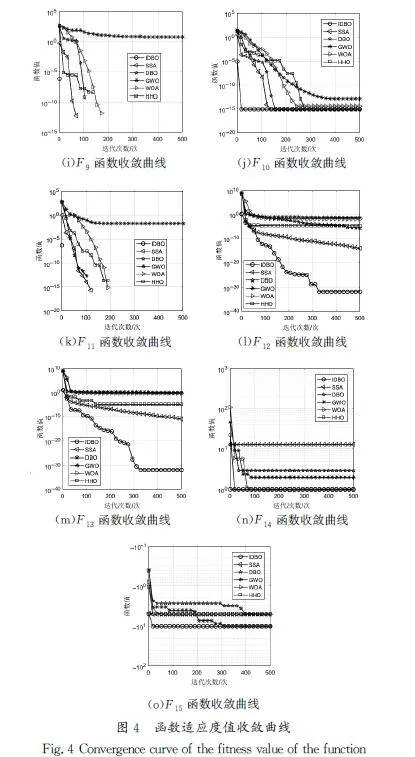
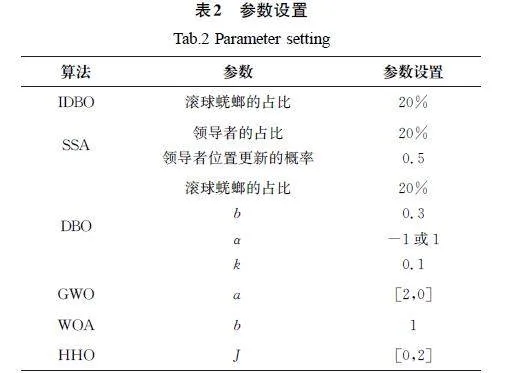
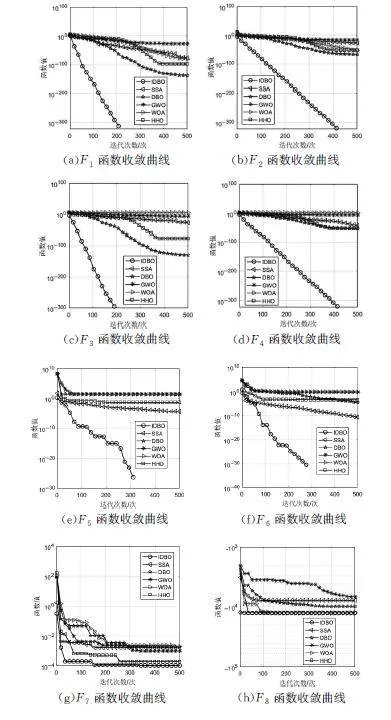
在本次实验中，所有算法的种群规模均设置为30，最大迭代次数设置为500次，为防止单次实验存在偶然性，将各算法均独立运行30次，然后取其最优值、标准差和平均值作为算法性能好坏的最终评定标准，其中最优值和平均值可以表征算法的收敛精度，标准差可以表征算法的稳定性。各算法性能的对比结果如表3所示（加粗部分表示各种算法的最优值），同时绘制算法的适应度收敛曲线图（图4），从中可以看出，改进后蜣螂优化算法的性能普遍优于其他对比算法的性能。

由表3可知，对于单峰测试函数F1～F7，由F1～F4和F6的最优值、标准差、平均值表明，IDBO算法的表现均优于其他算法，且这5个函数均能稳定地收敛到其最优解，而对于F5和F7，IDBO算法的性能虽然不是最好，但其各项指标均排在各算法的前列，并且F5的最优值得到了理论最优值。对于多峰测试函数F8～F13，IDBO算法的最优值、标准差、平均值相较于其他算法都表现为最小或者并列最小，其中F8、F9、F11达到了其理论最优值。对于固定多峰测试函数F14、F15，各种算法基本都能寻找到其最优值，但IDBO算法的标准差和平均值明显优于其他算法的相应指标值。综合来看，采用IDBO算法对15个基准测试函数进行求解寻优，其中有13个测试函数的求解结果优于其他各种对比算法的求解结果。通过上述分析可以看出，无论是对于单峰测试函数还是多峰测试函数，IDBO算法的大部分最优值和平均值都要优于其他对比算法的相应指标值，并且其标准差普遍小于其他算法。这表明经改进后的蜣螂优化算法较其他优化算法有着更高的寻优精度和稳定性。

从图4的数据分析中可以观察到，相较于其他对比算法，IDBO算法在大部分的基准测试函数上均展现出了优越的性能，具体表现为更快的收敛速度与更高的收敛精度。无论是对于单峰测试函数还是多峰测试函数，IDBO算法均能保持出色的表现，这说明改进后的蜣螂优化算法不仅能够快速收敛，还能够对函数解进行进一步的开发，即IDBO算法在全局探索能力与局部寻优能力之间找到了合理的平衡。

4结论（Conclusion）

针对蜣螂优化算法存在的收敛精度低、易陷入局部最优等问题，提出了一种改进的蜣螂优化算法，即IDBO算法。首先，在初始化种群阶段引入piecewise映射，增加其种群多样性；其次，在蜣螂滚球的无障碍前进阶段引入北方苍鹰优化算法的勘探策略，利用其对食物选择的随机性增强算法的全局勘探能力；再次，对蜣螂繁殖和觅食的边界收敛因子进行改进，使其收敛精度和收敛速度得到平衡；最后，在蜣螂觅食阶段引入自适应T分布扰动，进一步增强算法跳出局部最优的能力。通过在CEC2005基准测试函数集的15个函数上进行验证，IDBO算法相较于其他对比算法，展现出了最高的收敛精度、更快的收敛速度及更高的稳定性。

参考文献（References）

［1］XUEJK，SHENB.Dungbeetleoptimizer：anewmeta＼|heuristicalgorithmforglobaloptimization［J］.TheJournalofsupercomputing，2023，79（7）：7305＼|7336.

［2］远翔宇，杨风暴，杨童瑶.基于自适应蜣螂算法的无人机三维路径规划方法［J］.无线电工程，2024，54（4）：928＼|936.

［3］付雷，王骥.基于改进蜣螂优化算法的海洋牧场三维UWSN覆盖方法［J］.中山大学学报（自然科学版），2024，63（2）：115＼|122.

［4］赵鑫，王东丽，彭泓，等.基于多策略改进蜣螂算法优化的变压器故障诊断［J］.电力系统保护与控制，2024，52（6）：120＼|130.

［5］LIYH，SUNKX，YAOQ，etal.Adual＼|optimizationwindspeedforecastingmodelbasedondeeplearningandimproveddungbeetleoptimizationalgorithm［J］.Energy，2024，286：129604.

［6］郭琴，郑巧仙.多策略改进的蜣螂优化算法及其应用［J］.计算机科学与探索，2024，18（4）：930＼|946.

［7］ZHUF，LIGS，TANGH，etal.Dungbeetleoptimizationalgorithmbasedonquantumcomputingandmulti＼|strategyfusionforsolvingengineeringproblems［J］.Expertsystemswithapplications，2024，236：121219.

［8］DEHGHANIM，HUBLOVSKYS，TROJOVSKYP.Northerngoshawkoptimization：anewswarm＼|basedalgorithmforsolvingoptimizationproblems［J］.IEEEaccess，2021，9：162059＼|162080.

［9］XUEJK，SHENB.Anovelswarmintelligenceoptimizationapproach：sparrowsearchalgorithm［J］.Systemsscience&controlengineering，2020，8（1）：22＼|34.

［10］MIRJALILIS，MIRJALILISM，LEWISA.Greywolfoptimizer［J］.Advancesinengineeringsoftware，2014，69：46＼|61.

［11］MIRJALILIS，LEWISA.Thewhaleoptimizationalgorithm［J］.Advancesinengineeringsoftware，2016，95（C）：51＼|67.

［12］HEIDARIAA，MIRJALILIS，FARISH，etal.HarrisHawksoptimization：algorithmandapplications［J］.Futuregenerationcomputersystems，2019，97：849＼|872.