基于MATLAB平台的南京地铁1号线车站效用构建及改进措施

【摘 要】 采用MATLAB平台及DEA法构建城轨交通车站效用评价体系并对南京地铁一号线的车站效用进行评价，结果表明：所选南京地铁一号线的23个车站中，有8个车站的效用为DEA有效，其他15个车站存在某种程度的输入指标冗余或输出指标不足。经充分优化后，南京地铁一号线可通过合理配置车站的效用输入指标，提升其车站效用值。

【关键词】 MATLAB平台；DEA法；城轨交通；车站效用；输入指标；输出指标

Station Utility Construction and Improvement Measures of Nanjing Metro

Line 1 Based on MATLAB Platform

Ling Rui， Li Xue， Zou Shihuai， Xu Menghui， Jiang Feixiang*

（Nanjing Vocational Institute of Railway Technology， Nanjing 210031， China）

【Abstract】 This paper uses MATLAB platform and DEA method to construct the station utility evaluation system of urban rail transit， and studies the station utility of Nanjing Metro Line 1. The results show that among the 23 stations of Nanjing Metro Line 1， 8 stations have DEA effectiveness， and 15 stations have some degree of input index redundancy or output index insufficiency. After full optimization， the station utility value of Nanjing Metro Line 1 can be improved through reasonable allocation of station utility input index.

【Key words】 MATLAB platform; DEA method; urban rail transit; station utility; input index; output index

〔中图分类号〕 U2 〔文献标识码〕 A 〔文章编号〕 1674 - 3229（2024）03 - 0068 - 07

0 引言

城轨交通车站效用是影响城轨列车运行效率诸多环节中的重要一环。本文选取南京地铁1号线若干车站的部分效用指标，借助MATLAB平台及数据包络分析（Data Envelopment Analysis，DEA）法对南京地铁1号线各车站的效用构建评价体系，从而使南京地铁1号线的车站效用得以完善。

1 城轨交通车站效用评价体系及DEA法评价模型构建

1.1 城轨交通车站效用评价体系

常用的评价方法主要有客观评价法和主观评价法两大类。主观评价法主要有层次分析法、专家会议法、专家访谈法及德尔菲法（又称专家调查法）等。客观评价法包括运筹学及其他的数学方法，其中DEA是一种比较实用的方法。DEA法的评价特征如下：①非参数模型，DEA法致力于每个决策单元（Decision Making Unit，DMU）的优化而非对整体集合的统计回归优化；②切实有效的生产前沿面，DEA法改变了以往的评价方法中将非有效与有效混为一谈的局面，得出切实有效的生产前沿面；③多指标综合评价，DEA法可以同时考虑多项投入及产出的属性；④量纲无关性，使用DEA法前无需对数据进行无量纲化处理从而使得数据处理更具有弹性；⑤自评的相对客观性，DEA法可以让各DMU找到对自己最有利的权重以便尽可能提升该决策单元的效率；⑥改进效率的方向，DEA法可以区分出效率有待改进的决策单元和有效的决策单元，结合松弛变量分析和敏感性分析，为决策者提供各种改进效率值的可行途径［1］。

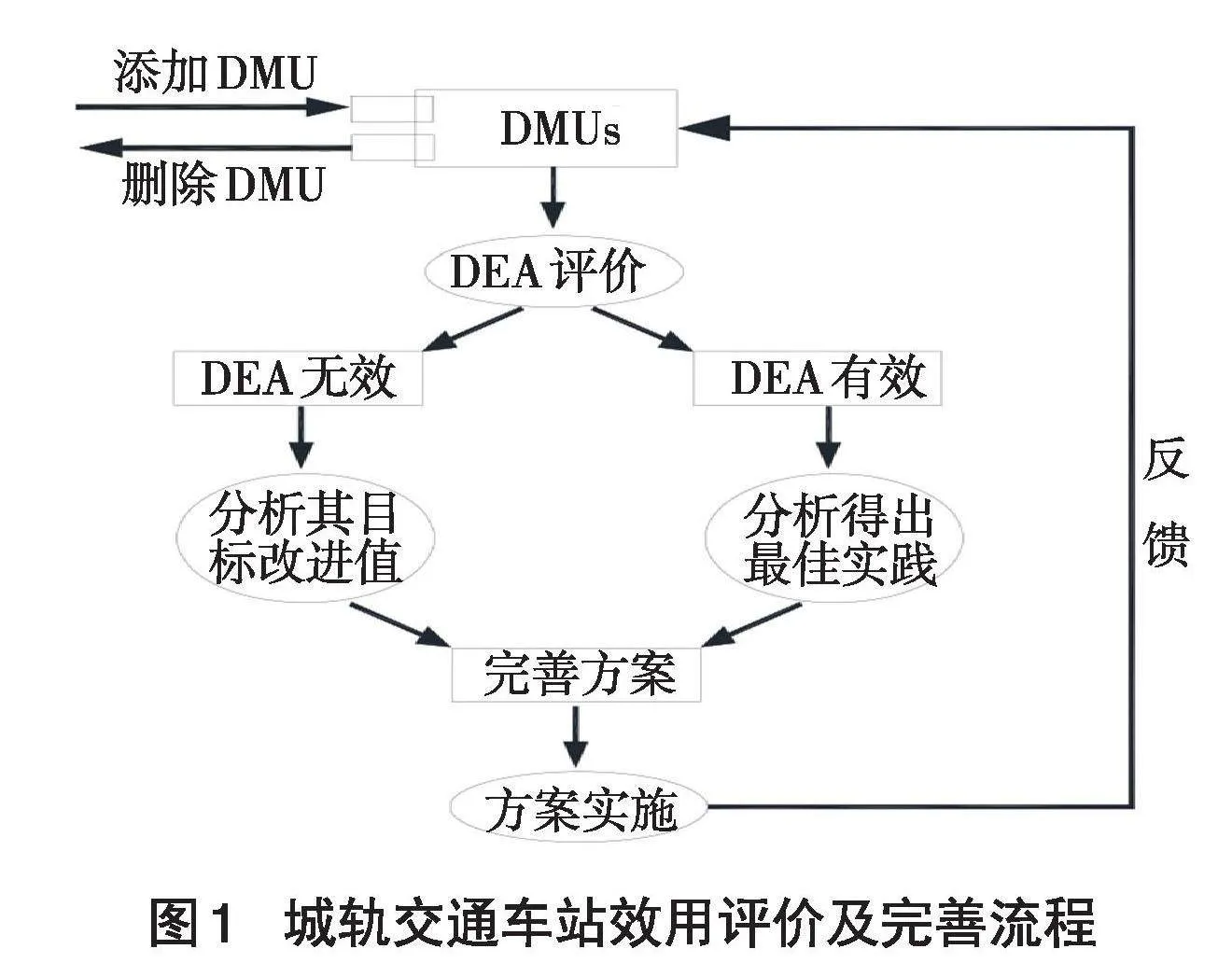
本文根据城轨交通车站服务的特点，选取一系列的输入及输出指标，以南京地铁1号线的若干车站为例，采用如下步骤进行效用评价。①运用DEA法对车站效用进行评价；②对效用“优秀”的车站（DEA有效）分析其效用最佳实践；③对效用“非优秀”的车站（非DEA有效）分析其目标改进值；④结合步骤②及③形成行之有效的完善方案并加以实施；⑤实施一段时间后应再次进行评价，具体流程如图1所示。

1.2 DEA法评价模型构建

1.2.1 DEA模型简介

DEA法是由Charnes、Cooper及Rhodes三位运筹学家提出［2］，是一种非参数分析法，主要用于综合评判分析，它使用线性规划来估计多个DMU的有效性，广泛应用于生产、管理学和经济学等领域。DEA法充分考虑了对于DMU本身最优的投入及产出方案，能够更合理地反映评价对象自身的信息及特点，对于评价复杂系统的多投入、多产出分析具有独到之处［3］。常用的DEA模型有Charnes-Cooper-Rhodes模型（简称CCR模型）和Banker-Charnes-Cooper模型（简称BCC模型）［4］。CCR模型是基于规模报酬不变的前提下考查DMU的总体技术效率即综合效率，反映DMU的规模效率及技术效率是否同时有效［5］。BCC模型是对CCR模型的扩充，是基于规模报酬可变的前提下将CCR模型的综合效率分为纯技术效率及规模效率，综合效率值均介于0～1之间；若综合效率值为1，则称DEA有效；若综合效率值小于1，则称DEA无效［6］。纯技术效率是因技术变化引起的效率变化，其值均介于0～1；若纯技术效率值为1，表示在现有的输入指标情况下，输出指标实现了最大化［7］。规模效率是指因规模变化而引起的效率变化，其值均介于0～1；若规模效率值为1，表示DMU的规模收益不变，即同等比例的输入指标数量带来同等比例的输出指标［8］。

DEA法中的CCR模型如式（1）所示：

[s.t.minθj=1nλjxj+S-=θx0j=1nλjyj-S+=y0λj≥0，j=1，2，…，nS-≥0，S+≥0] （1）

式中：[θ]表示第[n]个DMU的总效率值，据[θ]值的大小对DMU进行排序；若[θ]值等于1，表示该DMU为DEA有效，若[θ]值小于1，表示该DMU为非DEA有效。如果评价目标的DEA有效，表明输出指标与输入指标的比值较高，其适应性在评价样本中相对比较好。[S+]表示输入指标的松弛变量，[S-]表示输出指标的松弛变量。

1.2.2 DEA评价准则

（1）[θ]等于1且[S+]等于0及[S-]等于0，则该DMU为DEA有效，此状态下的DMU的经济活动既能满足规模有效又能满足技术有效。

（2）[θ]等于1且[S+]及[S-]中至少有一个大于0，则该DMU为弱DEA有效，此状态下的DMU的经济活动不会同时满足技术有效及规模有效。

（3）[θ]小于1，则该DMU为非DEA有效，该DMU的经济活动既无法满足规模有效又无法满足技术有效。

2 城轨交通车站效用评价指标体系的确定

2.1 城轨交通车站效用评价输入指标

（1）车站员工数量（单位：人）[x1j]：城轨交通车站在正常生产活动中处于管理岗和生产岗的总人数，包括地铁企业员工和委外人员（主要包括委外安检、委外保安、委外特勤、委外保洁和委外安全引导员等）两大部分，他们共同协作完成车站的运营生产工作。

（2）车站设备数量（单位：台/套/部）[x2j]：城轨交通车站在正常生产活动中专供乘客进站乘车及下车出站的机电设备，包括自助充值机、自动售票机、闸机、电扶梯和直升电梯等的总数量。

（3）车站用电量（单位：千瓦*时/日）[x3j]：城轨交通车站的用电量主要包括动力用电量和商业用电量两部分；其中，动力用电量主要由照明插座用电量、通风空调用电量（在用电量中所占的比例最大且随季节变化比较大，通常取平均值）、电扶梯（或直升电梯）用电量和特殊（主要包含银行自助机及商铺） 用电量4部分组成。

2.2 城轨交通车站效用评价输出指标

（1）车站提供进站乘车服务人数（单位：人/时）[y1j]：城轨交通车站提供进站乘车服务的流程是①通过楼梯（或电扶梯）进入站厅“非付费区”；②通过自动售票机购买单程票（若乘客持有公共交通卡或手机电子卡，此步骤可略）；③通过进站闸机进入车站“付费区”；④通过楼梯（或电扶梯）进入站台候车；⑤列车进站停稳后乘客上车。

（2）车站提供乘客出站服务人数（单位：人/时）[y2j]：城轨交通车站提供乘客出站服务的流程是①列车到站停稳后乘客下车进入站台；②通过楼梯（或电扶梯）进入站厅；③通过出站闸机进入车站“非付费区”；④通过楼梯（或电扶梯）出站。

（3）车站提供残疾人服务次数（单位：次/月）[y3j]：城轨交通车站提供残疾人服务主要体现在①在车站的地面至站厅、站厅至站台处设置垂直电梯；②垂直电梯的按键均设置盲文；③站外垂直电梯周边设置轮椅坡道；④车站的出入口、通道、站厅、站台等公共区域均设置盲道；⑤站内明显位置处张贴无障碍标识等方面。

（4）乘客忠诚度值（单位：百分制分值）[y4j]：乘客忠诚度具体是指因乘行的质量、价格、服务等诸多因素的影响而使得乘客对某一交通企业的产品（或服务）产生感情，进而形成偏爱并长期重复购买该企业的产品（或服务）的程度［9］。城轨交通车站乘客忠诚度评价包括①进出站；②秩序与环境；③设施运行；④换乘；⑤咨询；⑥投诉；⑦安全感等7个评价指标，根据乘客忠诚度评价内容设计调查问卷，评价量表宜采用5级文字量表和数字量表（详见表1），评价模型如式（2）所示。

[z=i=1nδi*Si] （2）

式中：[z]—乘客忠诚度，[n]—乘客忠诚度评价指标的数量，[δi]—第i项指标的权重值（满足[i=1nδi=1]），[Si]—第i项指标的忠诚度体验值（通常经过调查问卷调查后，5级量表分值[xi]采用公式[Si=xi-15-1*100%]转化为百分制分值[Si]）。

3 DEA法评价在MATLAB平台上的程序实现

MATLAB是由Mathworks公司采用C语言编写的著名工程数学应用软件［10］，DEA（基于CCR模型）法评价在MATLAB平台（基于MATLAB R2016a版本）的程序分为两部分，具体如下。

3.1 DMU综合效率评价程序

1.%先将输入指标及输出指标以‘shuru.xlsx’及‘shuchu.xlsx’文件形式保存在‘MATLAB＼R2016a＼bin’下

2.clear all;clc;

3.I=xlsread（′shuru.xlsx′，1，′A1：W3′）;

4.O=xlsread（′shuchu.xlsx′，1，′A1：W4′）;

5.if sum（sum（I<=0））>0; %检查输入指标是否正确

6.ERROR=1;

7.display（′输入指标错误！请仔细核对输入指标！！′）

8.elseif sum（sum（O<=0））>0; %检查输出指标是否正确

9.ERROR=2;

10.display（′输出指标错误！请仔细核对输出指标！！′）

11.else

12.end

13.a=size（I′，1）;

14.b=size（I，1）;

15.c=size（O′，1）;

16.A=［-I′ O′］;

17.d=zeros（a，1）;

18.lb=zeros（b+d，1）;

19.ub=［］;

20.for i=1：b;

21.e=［zeros（1，b） -O（：，i）′］;

22.Aeq=［I（：，i）′ zeros（1，c）］;

23.beq=1;

24.w（：，i）=linprog（e，A，d，Aeq，beq，lb，ub）; %解线性规划，得到DMUi的最佳权向量wi

25.E（i，i）=O（：，i）′*w（b+1：b+c，i）;

26.end

27.w %输出最佳权向量

28.E %输出相对效率值Eii

29.omega=w（1：b，：） %输出投入权向量

30.mu=w（b+1：b+c，：） %输出产出权向量

3.2 DMU最优解程序

1.%先将输入指标及输出指标以‘shuru.xlsx’及‘shuchu.xlsx’文件形式保存在‘MATLAB＼R2016a＼bin’下

2.clear all;clc;

3.I=xlsread（′shuru.xlsx′，1，′A1：W3′）;

4.O=xlsread（′shuchu.xlsx′，1，′A1：W4′）;

5.if sum（sum（I<=0））>0; %检查输入指标是否正确

6.ERROR=1;

7.display（′输入指标错误！请仔细核对输入指标！！′）

8.elseif sum（sum（O<=0））>0; %检查输出指标是否正确

9.ERROR=2;

10.display（′输出指标错误！请仔细核对输出指标！！′）

11.else

12.end

13.a=size（I，1）;

14.c=size（I′，1）;

15.d=size（O′，1）;

16.epsilon=10^-10;

17.f=［zeros（1，a） -epsilon*ones（1，c+d） 1］;

18.A=zeros（1，a+c+d+1）;b=0;

19.lb=zeros（a+c+d+1，1）;ub=［］;

20.lb（a+c+d+1）=-Inf;

21.for i=1：c;

22.Aeq=［I eye（c） zeros（c，d） -I（：，i）

23.O′ zeros（d，c） -eye（d） zeros（d，1）］;

24.beq=［zeros（c，1）

25.O（：，i）］;

26.w（：，i）=linprog（f，A，b，Aeq，beq，lb，ub）; %得到DMUi的最佳权向量wi

27.end

28.w %输出最佳权向量

29.lambda=w（1：a，：）%输出各DMU的组合系数

30.s_minus=w（a+1：a+c，：） %输出输入指标的松弛变量

31.s_plus=w（a+c+1：a+c+d，：） %输出输出指标的松弛变量

32.theta=w（a+c+d+1，：） %输出各DMU的相对效率值

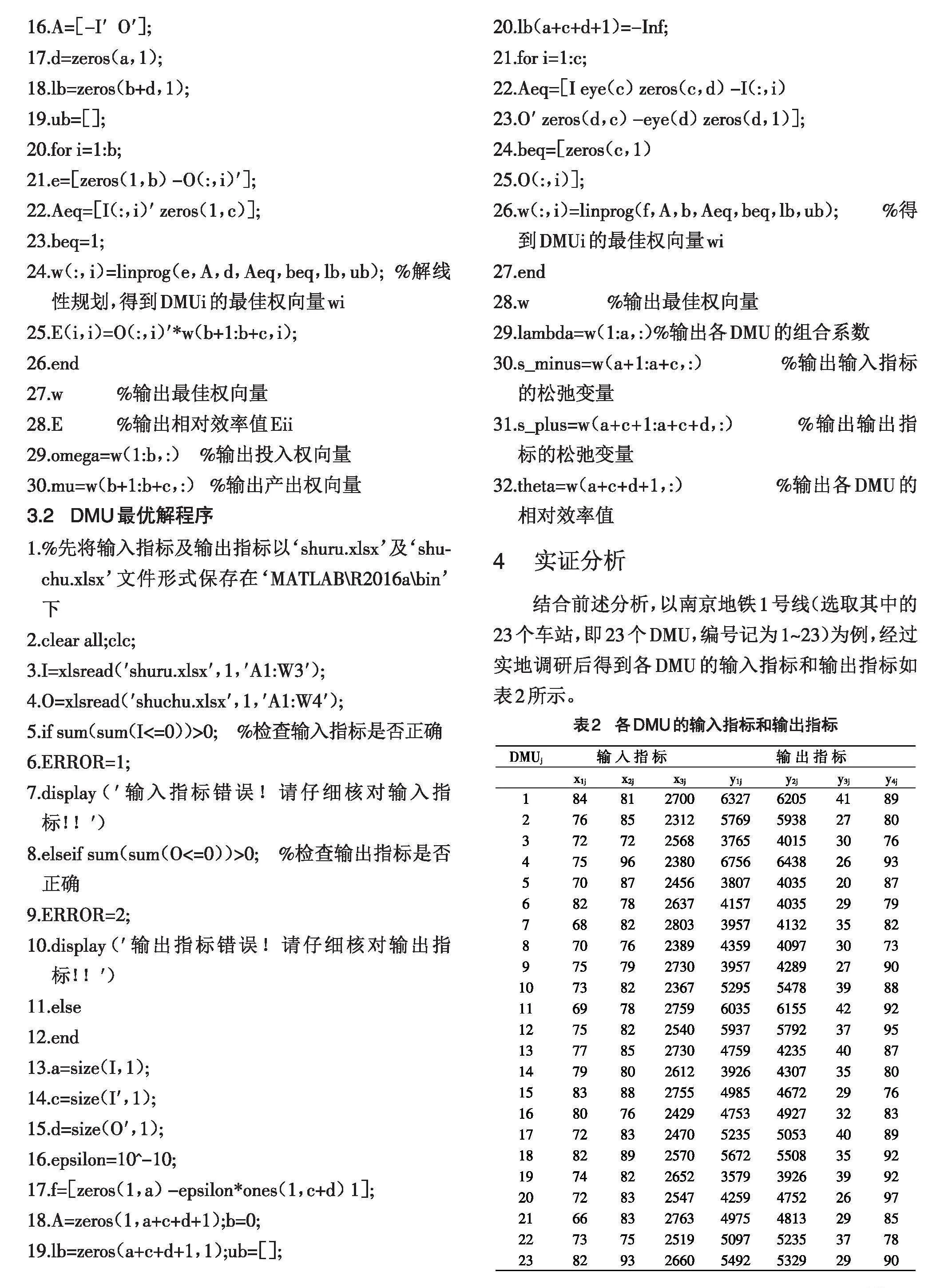
4 实证分析

结合前述分析，以南京地铁1号线（选取其中的23个车站，即23个DMU，编号记为1～23）为例，经过实地调研后得到各DMU的输入指标和输出指标如表2所示。

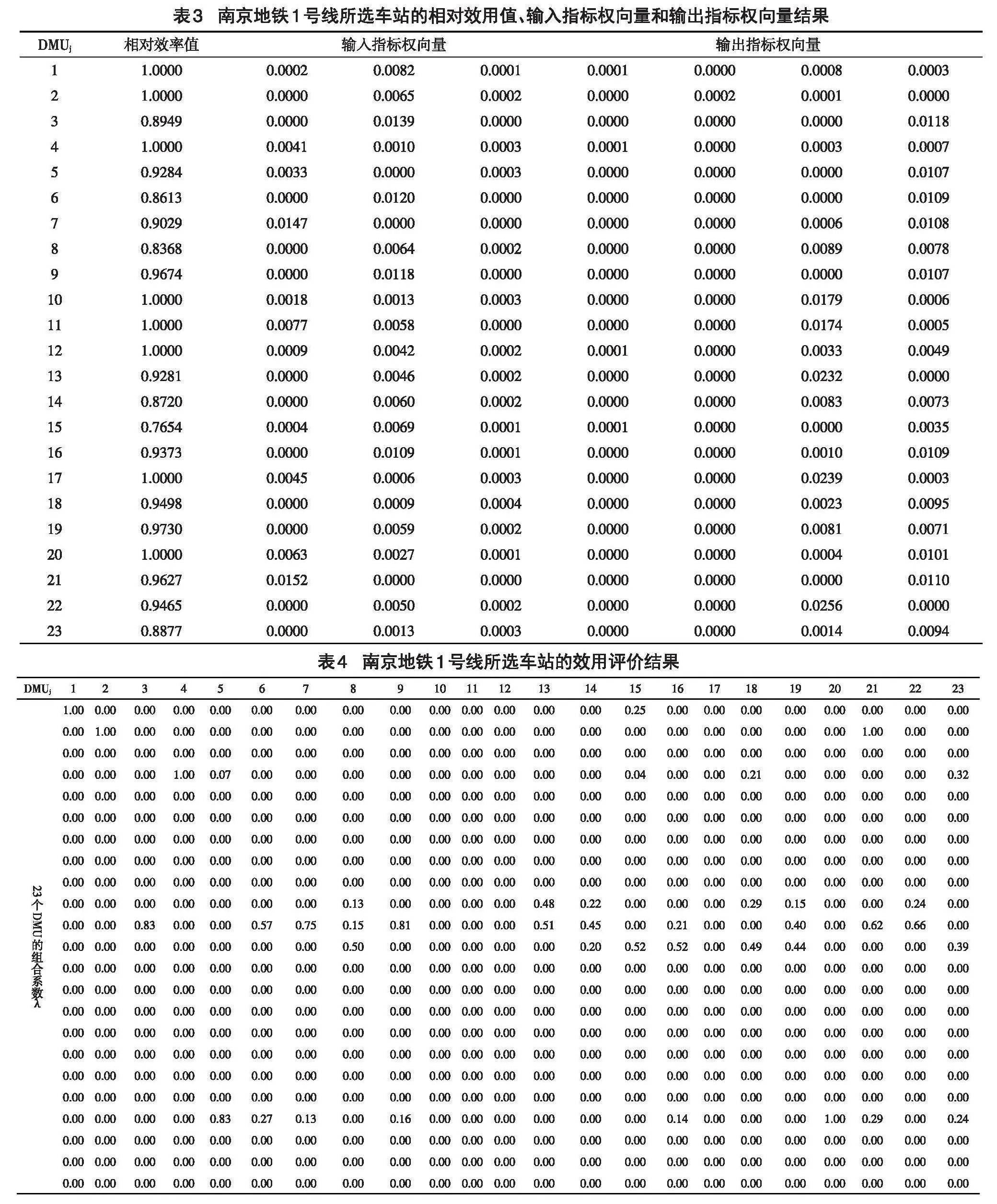
采用前文的MATLAB平台程序3.1得到所选的南京地铁1号线23个车站的相对效用值及输入指标的权向量和输出指标的权向量，具体如表3所示。

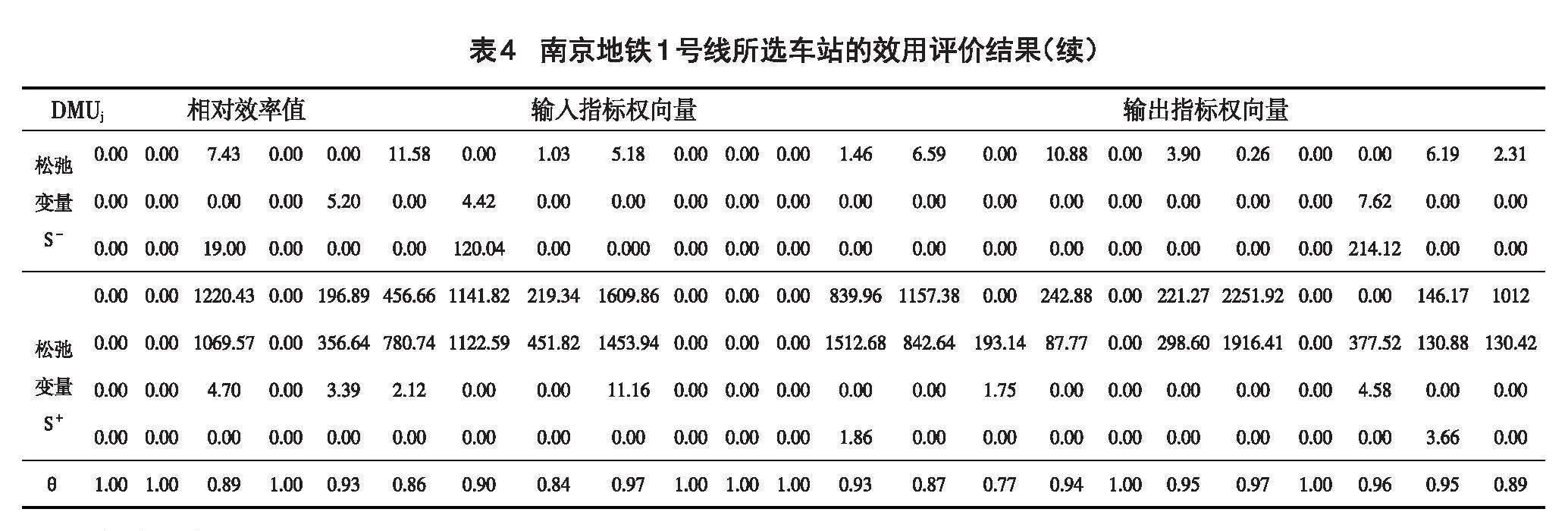
显然，DMU1，DMU2，DMU4，DMU10，DMU11，DMU12，DMU17和DMU20至少是弱DEA有效，其余各DMU为非DEA有效。为进一步确认DMU1，DMU2，DMU4，DMU10，DMU11，DMU12，DMU17和DMU20的有效性并分析其余各DMU的非DEA有效原因，需用MATLAB平台程序3.2，其结果如表4所示。

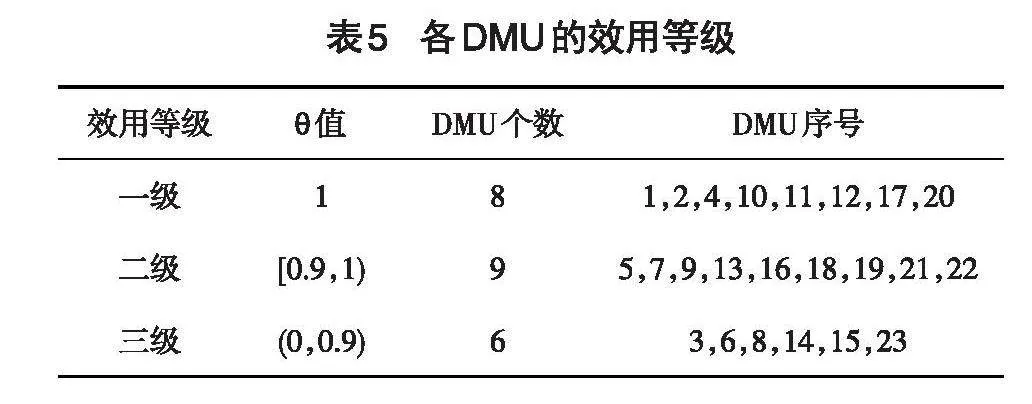
由表4知，DMU1，DMU2，DMU4，DMU10，DMU11，DMU12，DMU17及DMU20共8个车站的DEA相对有效值[θ]均为1且输入指标的松弛变量S-和输出指标的松弛变量S+均为0，由DEA评价准则可知这8个车站的效用为DEA有效，车站的经济活动同时满足技术有效和规模有效；剩余的15个车站效用为非DEA有效，这些车站的经济活动既无法实现技术有效也无法实现规模有效。车站的DEA相对有效值[θ]的大小也表明了各车站的效用水平的高低，显然，车站DMU15的效用值最低（仅为0.77）。以[θ]=0.90作为分界点，可将这23个车站划归为3个等级，具体如表5所示。

对于有效值[θ]小于1的车站，可以采取如下两项措施：（1）减少输入指标的量却可以保持原有的输出指标的量；（2）在保持原有输入指标量的前提下采取适当措施以增加输出指标的量。对于输入指标而言，理论输入指标量=实际输入指标量[−]输入指标的松弛变量S-；对于输出指标而言，理论输出指标量=实际输出指标量[+]输出指标的松弛变量S+。以车站DMU6为例，在当前的PF且参考集不变的情况下，车站员工数量的目标改进值为（82-11.58=70.42）≈70人。以决策单元DMU21为例，根据DEA有效的经济活动意义［11］，基于各项输出指标量均维持不变的条件下，构建新的[DMUNEW21]，即：

可使得[DMUNEW21]的输入指标比例减少到原输入指标量的0.96（DMU21的[θ*]）倍，而且（由输入指标的松弛变量[S-]和输出指标的松弛变量[S+]知）还可以进一步减少车站设备数量近8（实际值为7.62）台/套/部，减少车站用电量近214（实际值为214.12）千瓦*时/日，增加车站提供乘客出站服务人数近378（实际值为377.52）人/时，增加车站提供残疾人服务次数5（实际值为4.58）次/月。

通过对效用为DEA有效的8个车站进行仔细考察，发现导致高效用的主要原因是DMU1，DMU2，DMU10，DMU12和DMU20的车站员工数量与车站设备数量匹配程度相当，而DMU4，DMU11和DMU17采用了合理控制商业用电量的方式以达到有效减少车站用电量的目标，效果相当显著。

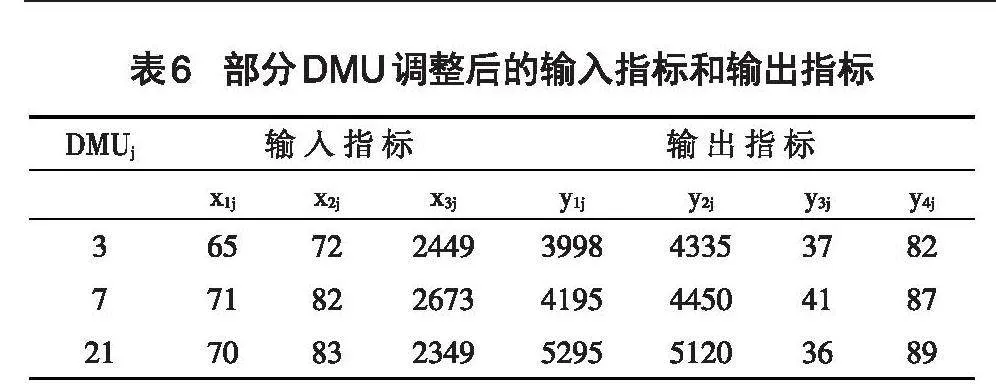
由于DMU3，DMU7及DMU21的效用为非DEA有效，DMU3的车站员工数量冗余近7人，车站用电量冗余19千瓦*时/日，DMU7的车站设备数量冗余近5台/套/部，车站用电量冗余近120千瓦*时/日，DMU21的车站设备数量冗余近8台/套/部，车站用电量冗余接近214千瓦*时/日。为了将高效的车站效用运用到效用较差（效用为非DEA有效）的车站，措施如下：将DMU3的明显冗余的员工调配3人去DMU7，调配4人到DMU21，在此基础上DMU3，DMU7及DMU21在保证车站设备正常运转的前提下合理控制商业用电量以达到有效减少车站总用电量的目标。运行一段时间后，重新考察DMU3，DMU7及DMU21的输入指标和输出指标，详情见表6。

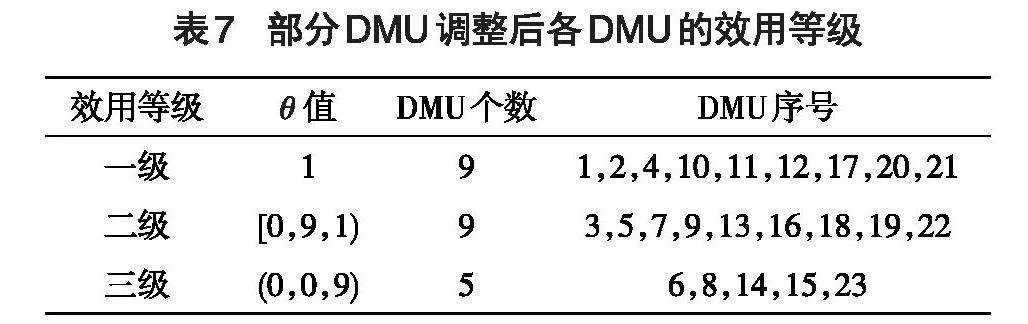
假定其余各DMU的输入指标和输出指标均未变化，重新使用MATLAB平台程序得到各城轨交通车站效用评价结果，依旧以[θ∗]=0.90作为分界点将这23个车站划归为3个等级，具体如表7所示。

观察表7可以发现：此时的车站效用DEA相对有效值和PF均发生了变化。DMU21由调整前的效用等级二级的非DEA有效跃升为调整后的效用等级一级的DEA有效，成为“标杆车站”，DMU3由调整前的效用等级三级的非DEA有效跃升为调整后的效用等级二级的非DEA有效，DMU7在调整前与调整后的效用等级均为二级的非DEA有效，但其DEA相对有效值[θ]由调整前的0.9029跃升为调整后的0.9840，已经很接近效用等级为一级的DEA有效。其余各DMU由于相对效用此消彼长，有些轻微的变动，可以在各车站中逐步推广车站效用最大化的经验。

5 结语

本文采用MATLAB平台结合具体案例研究了DEA法在城轨交通车站效用评价及改进中的应用，结果显示，使用DEA法可以相当直观地找出“效用标杆”车站及“效用差距”，从而发现改进效用的最佳途径。

当前的研究不足之处是范围仅限于在南京地铁1号线的若干车站间寻找“效用标杆”，随着新设备及先进管理经验的逐步推广，各车站的相对效用值将会逐渐趋同，届时，应当及时引入外部车站的“效用标杆”，进一步扩大生产前沿面，从而实现车站效用的持续改善。

［参考文献］

［1］ 杜栋，庞庆华.现代综合评价方法与案例精选［M］.北京：清华大学出版社，2005：64-67.

［2］ 孙健.广西乙类大型医用设备利用效率评价［J］.智慧健康，2018，4（2）：27-29.

［3］ 黄国兴，杨泽铭，卢为党，等.利用粒子滤波方法求解数据包络分析问题［J］.计算机科学，2022，49（S1）：159-164.

［4］ 马其波，靳聪，康霓，等.基于DEA-TOPSIS组合模型的大型医疗设备利用效率综合评价研究［J］.中国医疗设备，2020，35（8）：122-125.

［5］ 冯晶晶，徐笑，乔冠华，等.基于数据包络分析的县级医院眼科服务效率研究［J］.中国医院管理，2021，41 （4）：43-46.

［6］ 许轲，何瑞仙，邱亭林.应用数据包络分析法评价手术科室运营效率［J］.中国卫生统计，2022，39（2）：260-262.

［7］ 刘利，王楠，武爱文.医改背景下基于DEA的医院科室运行效率评价［J］.中国卫生统计，2019，36（5）：724-727.

［8］ 陈聚祥.福建省县级公立医院改革试点运行效率分析-基于DEA模型的实证分析［D］.天津：天津医科大学，2016.

［9］ 吕宇栋.基于RFM模型的网络客户忠诚度研究［J］.哈尔滨职业技术学院学报，2013（3）：48-49.

［10］黎红，张昊龙.基于联合贝叶斯算法的人脸匹配算法的Matlab实现［J］.廊坊师范学院学报（自然科学版），2016，16（1）：31-34+41.

［11］许露露.基于DEA方法的精准扶贫效率区域差异及其影响因素分析［J］.廊坊师范学院学报（自然科学版），2020，20（2）：82-90.

责任编辑 吕荣荣

［收稿日期］ 2024-03-16

［基金项目］ 江苏省教育厅创新创业培育计划项目（G-2023-1206）

［作者简介］ 凌睿（2004- ），男，南京铁道职业技术学院学生，研究方向：城市轨道交通运营管理。

［通讯作者］ 蒋飞翔（1981- ），男，硕士，南京铁道职业技术学院讲师，研究方向：城市轨道交通运营管理。