基于同态加密的数据库信息安全应用研究

摘 要：随着信息化技术的发展，涉及到个人信息的数据规模也在增加，如果大量的个人信息泄露，不仅会导致用户生命财产受损，更会破坏市场秩序、制约经济发展，甚至会引发公共安全危机。该研究旨在保护本地数据库安全，采用Paillier同态加密算法对数据库进行加密。通过测试，可以实现对指定数据库、表及字段进行加解密操作，有效防范他人对本地数据库数据的恶意窃取泄露，提高用户本地计算机的安全性，保护用户数据隐私。

关键词：信息安全;数据库;同态加密;Paillier算法;系统测试

中图分类号：TP391.1 文献标志码：A 文章编号：2095-2945（2024）30-0080-04

Abstract： With the development of information technology， the scale of data involving personal information is also increasing. If a large amount of personal information is leaked， it will not only cause damage to users' lives and property， but also destroy market order， restrict economic development， and even trigger a public security crisis. This research aims to protect the security of the6Wx7iN8GBxfINba59nrFKA== local database and uses the Paillier homomorphic encryption algorithm to encrypt the database. Through testing， encryption and decryption operations on specified databases， tables and fields can be realized， effectively preventing others from malicious theft and disclosure of local database data， improving the security of users' local computers， and protecting user data privacy.

Keywords： information security; database; homomorphic encryption; Paillier algorithm; system testing

随着信息化的发展，数据规模的增长，保护数据安全是当下需要重视的。目前，保障数据库安全的主要途径包括身份验证、防火墙等，但数据泄露仍频繁发生，证明仅有的这些措施不足以解决问题。

为保护数据库安全，使合法用户安全访问数据，最有效的途径还是数据加密。数据加密可以有效避免数据的非法访问，防止数据遭遇不法侵入。本设计旨在通过同态加密技术对关键数据库中数据进行加密处理，实现数据保护。

1978年，Rivest等人第一次提出秘密同态技术[1-4]，他们发现其可以处理密文间的直接运算问题。ElGamal和Paillier又分别于1984年和1999年提出弱同态加密算法，ElGamal算法属于乘法同态加密算法，其安全性由有限域上的离散对数的计算难题决定;Paillier算法具有加性同态，它的安全性基于复合剩余类的问题的确定，它们都因为加入随机数的选择具备更高的安全性。2009年，Gentry提出基于理想格和整数的第一代全同态加密方案，但由于效率因素，没有办法应用到实际中。经过优化后，Gentry等人又在2011、2012年提出基于RLWE和LWE的第二代全同态加密方案。

1 同态加密算法实现

1.1 相关介绍

Paillier加密算法是一种概率公钥加密算法[5-6]，基于复合剩余类的困难问题且满足加法同态和数乘同态，也就是密文的乘积等价于明文的和

。 （1）

1.2 算法原理

密钥生成算法[7]（keyGeneration）：使2个随机素数p，q满足gcd（pq，（p-1）（q-1））=1，然后计算n=pq和λ=lcm（p-1，q-1），选择随机整数g∈Z，Z就是小于n2 且与n2互质的正整数集合。其中（n，g）做为公钥，λ做为私钥。

加密算法（encryption）：选择随机数r，满足0<r<n且r∈Z，即r在n2的剩余系下存在乘法逆元，输入明文m，0≤m<n，然后计算出密文

。 （2）

解密算法（decryption）：计算出明文m，其中L（u）= ，

1.3 要点解析

1.3.1 快速幂取模

朴素方法中计算abmodc，若a、b为较大数，会非常消耗计算资源，产生的中间数也会非常大，无法记录。对于取模运算，存在（a×b）modc=（（amodc）×（bmodc））modc成立，即将大数的幂运算拆解为对应的乘法运算，原理为对任意的整数模幂运算abmodc，可以将b拆成二进制形式，得b=b0+b1×2+b2×22+…+bn×2n，如此ab=a×a×…×a，b的值只能为0或1，其中bx=0的项计算结果为1可以不用考虑，则abmodc就可以转换为（amodc）×…×（amodc），每一项总为前一项的平方倍，得出以下结论[8]。

b为偶数，记k=a2modc，求（k）（b/2）modc即可，b为奇数，直接求（（（k）（b/2）modc）×a）modc。

1.3.2 扩展欧几里得算法

欧几里得算法：存在2个数a，b求它们的最大公约数，可以使用gcd（a，b）=gcd（b，a%b）。还需用到裴蜀定理：如果a，b是整数，那么一定存在整数x、y使得ax+by=gcd（a，b），如果ax+by=m有解，那么m一定会是gcd（a，b）的若干倍。通过扩展欧几里得算法，除了能求出最大公约数，还可以实现裴蜀定理求出通解x，y，而当gcd（a，b）=1时，就能够求出一个特殊通解：a对d的乘法逆元。应用到paillier算法中，就能够选取出符合规定的r，r∈Z。

1.3.3 素性检测

判断一个数是否为素数，可以用试除法。但涉及到大整数检测，其数位每增加一位，相对于试除法其运算需增加一个指数级别，所以一般使用Miller-Rabin算法[7-9]，使用此算法需了解2个理论基础，①费马小定理：当p为质数，有ap-1≡1（modp），反之不一定成立。②二次探测：如果p为素数，0<x<p，则方程x2≡1（modp）的解为x=1或x=p-1。

2 设计与实现

2.1 总体设计

软件流程图如图1所示。

2.2 加解密实现

加密字段：查询后与连接变量传入数据集遍历，实现行数据控制。遍历过程中，将预加密字段作为参数控制列，将每行数据作为明文参数进行加密。加密表：查询表所有字段，控制各列数据。外层遍历与加密字段一致，再遍历字段完成列数据控制实现整表加密。加密数据库：查询数据库中表为最外层循环，实现表操作，其余逻辑与加密表一致。

解密操作：操作逻辑与加密相同，调用密文解密算法即可。

3 系统测试

本节以加解密时间为性能指标进行测试，以每毫秒处理数据为基准对比得出效率。（注：数据库包含2张表：信息表和就诊表，对数据1 000、2 000、4 000行时进行效率测试）。

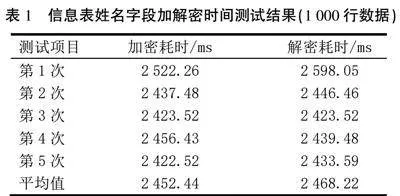
信息表中的姓名字段加解密效率测试（1 000行数据）。加密效率：0.407 8行/ms;解密效率：0.405 2行/ms（见表1）。

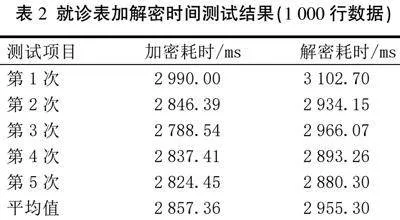
医院数据库中就诊表加解密效率测试（1 000行数据）。加密效率：0.350 0行/ms;解密效率：0.338 4行/ms（见表2）。

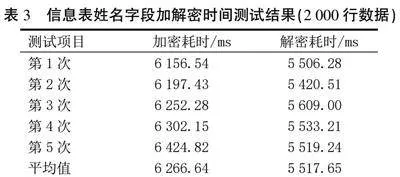
信息表中的姓名字段加解密效率测试（2 000行数据）。加密效率：0.319 2行/ms;解密效率：0.362 5行/ms（见表3）。

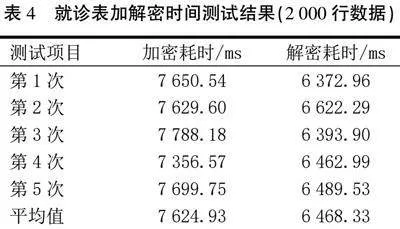
医院数据库中就诊表加解密效率测试（2 000行数据）。加密效率：0.262 3行/ms;解密效率：0.309 2行/ms（见表4）。

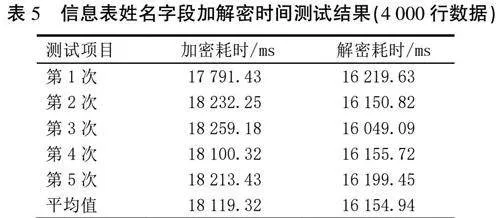
信息表中的姓名字段加解密效率测试（4 000行数据）。加密效率：0.220 8行/ms;解密效率：0.247 6行/ms（见表5）。

医院数据库中就诊表加解密效率测试（4 000行数据）。加密效率：0.173 8行/ms;解密效率：0.212 4行/ms（见表6）。

通过对比表1—表6中数据，我们发现，随着样本量增加，加解密操作耗时增加，每毫秒处理的数据量减少，也就意味着随着数据量提升，加解密操作效率会下降，且样本量越大，加解密效率会越来越低，但是整个过程不会出现加解密错误丢失数据的现象。

4 结束语

本文主要研究同态加密算法在数据安全的测试应用，通过对数据库2a745d74184d1a4fd50760ad71b7e3d7实施安全加密操作来保证数据安全。通过此次研究，也发现其加密的效率与安全性方面也存在一些不足。

1）同态加密算法的加解密效率，如果明文的数值过于大，其效率偏低。

2）Paillier算法中随机数g是趋于0到2个大质数乘积的平方且与其互质，如果在解密过程中L（gλmodn2），即分母上的值对n取模后为2个大质数p、q中任一数的倍数，就会存在乘法逆元，只能舍弃。所以在选取g时，范围限定内的部分值不能使用，需优化算法。

参考文献：

[1] 宋天煜.面向密文数据库的中间件系统的设计与实现[D].南京：南京邮电大学，2019.

[2] 李雅囡.基于同态加密的电子评分系统的研究与实现[D].沈阳：辽宁大学，2019.

[3] 李增鹏，邹岩，张磊，等.一种基于全同态加密的智能电网数据交换隐私保护方案[J].信息网络安全，2016（3）：1-7.

[4] 黄保华，王添晶，贾丰玮.数据库中数值型数据的加密存储与查询方法[J].计算机工程，2016，42（7）：123-128.

[5] 杨燕莉.基于同态加密的结构化数据库安全检索方案研究[D].武汉：武汉理工大学，2017.

[6] 冯超.全同态加密的相关算法研究[D].济南：山东大学，2015.

[7] RIVEST R L， ADLEMAN L， DERTOUZOS M L. On data banks and privacy homomorphisms[J]. Foundations of Secure Computation， 1978：169-179.

[8] DIJK M V， GENTRY C， HALEVI S， et al. Fully Homomorphic Encryption over the Integers[C]// Annual International Conference on the Theory and Applications of Cryptographic Techniques. Springer， Berlin， Heidelberg， 2010.

[9] PAILLIER P. Public-key cryptosystems based on composite degree residuosity classes[C]//International Conference on Theory & Application of Cryptographic Techniques.1999.

基金项目：甘肃省科技计划项目-重点研发计划-工业类（23YFGA0032）

第一作者简介：李怀堂（2000-），男，研究实习员。研究方向为计算机科学。