基于Monte Carlo的风力机叶片强度可靠性分析

摘 要：随着风力机应用数量增多，以及应用规模扩大，风力机叶片可靠度的保证尤为关键。利用Monte Carlo客观分析叶片强度可靠性，为叶片安全状态长效维持提供依据，实现风力机的平稳运转。该文在介绍Monte Carlo的基础上，分析风力机类型及其叶片状态和叶片参数，并以有限元模型构建的方式分析风力机叶片载荷及强度，最后探究基于Monte Carlo的风力机叶片可靠性。

关键词：Monte Carlo;风力机;叶片强度;可靠性分析;有限元模型

中图分类号：TK83 文献标志码：A 文章编号：2095-2945（2024）30-0060-04

Abstract： As the number of wind turbine applications increases and the scale of applications expands， ensuring the reliability of wind turbine blades is particularly critical. Monte Carlo is used to objectively analyze blade strength reliability to provide a basis for long-term maintenance of blade safety conditions and achieve smooth operation of wind turbines. Based on the introduction by Monte Carlo， this paper analyzes the types of wind turbines， their blade states and blade parameters， analyzes the load and strength of wind turbines blades by means of finite element model construction， and finally explores the reliability of wind turbines blades based on Monte Carlo.

Keywords： Monte Carlo; wind turbine; blade strength; reliability analysis; finite element model

风力机叶片物理故障客观存在，为减少叶片弯矩失效事件，务必对叶片强度可靠性分析。当Monte Carlo用于分析风力机叶片强度及可靠性，基于有限元模型掌握额定风速、切出风速2种工况下叶片的失效概率和变异系数。根据0.000 28（0.000 35）较低失效概率和14.2%（18.7%）较低变异系数，选定精确度高、适用性强的子集模拟法展开分析。

1 Monte Carlo概述

Monte Carlo中文名称为蒙特卡洛模拟法，是结构可靠度分析法的一种。Monte Carlo程序结构简单，受几何条件影响甚微，易于实现[1]。其应用原理，即围绕随机事物特点进行接近真实性的描述，并逼真模拟物理实验过程，误差、精度易确定。这一方法计算公式如公式（1），以随机试验的形式计算积分，分布密度函数用f（r）表示，随机变量用g（r）表示，视所计算积分为函数中自变量的数学期望。

<g>=g（r）f（r）dr 。 （1）

试验中，若干观察值r1、r2……rN指函数中f（r）的N个子样;对应观察值的随机变量值，用g（r1）、g（r2）、g（rN）表示，随机变量值的算数平均值（公式（2））又可称为积分近似值。

gN=∑g（ri）。 （2）

Monte Carlo在可靠性分析中能够提供精确解，但要以模拟次数为依据，围绕失效率值分析模拟数量，当失效率小于0.001，说明模拟数量之多。一般来说， Monte Carlo抽样次数在102～104 pf之间，但耗时较长，不易实现。因此，要想获得Monte Carlo高精度解，要借助适当方法选择适合样本。当Monte Carlo用于风力机叶片强度可靠性分析，考虑到风力机叶片弯矩失效事件的失效率偏低，模拟次数约100万次，为减少工程量，可在Monte Carlo方法上开发减方差方法——子集模拟法[2]。

2 风力机类型及其叶片

2.1 风力机类型

以结构为依据对风力机分类，一般而言，风力机由叶片、转子、齿轮箱、定子、变桨系统和发电机等组成，在组成机构的协作下实现空气动能向机械能的转化，其中，叶片获取风能，并向转子机构传力[3]。齿轮箱连接低速轴和高速轴，通过转速切换驱动发电机工作。

2.2 叶片状态

风力机叶片是风轮的重要部件，叶片工作强度、工作稳定性影响风力机性能，当叶片可靠性得到保证，则风力机故障率会大大降低，进而实现风力机常态化运转[4]。由于风力机大多处于野外区域、沿海区域，风力较大、风速较快，极易导致叶片受损、失效，所以要增强叶片抗失效能力，确保叶片强度，使其达到安全状态。叶片强度、叶片应力属于叶片结构分析变量，用Xi表示，则Z是Xi函数，通过特定概率模型进行变量表达，叶片结构失效概率用Pf表示，公式如下

Pf=P（Z<0） 。 （3）

叶片可靠度指既定时间内和已有条件下，完成预定功能的概率，用1-Pf表示。针对风力机叶片状态判断的过程，即叶片强度可靠性分析的过程。

2.3 叶片参数

风力机叶片数量受风机转速、风轮尖速比2个因素影响，一般情况下，水平轴向风力机处于高速状态，尖速比在5～15之间，叶片数目2～4或1～2片。

叶轮平面直径（D）用公式（4）计算

P=·η1·η2=0.49VDCp η η，（4）

式中：P为输出功率，V1为设计风速，ρ为设计风速，η、η分别代表发电机效率和传动效率，Cp表示风能利用系数。

叶尖速比（λ0）用公式（5）表示

λ0= ， （5）

式中：ω、R分别表示风力机叶轮旋转角速度和叶轮圆平面半径，V1代表叶轮设计风速。

3 风力机叶片建模分析

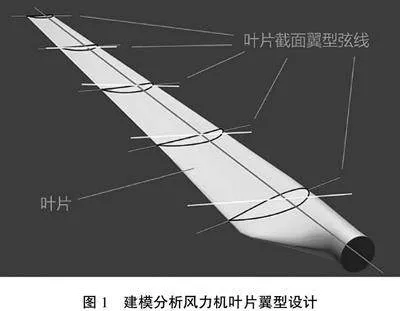
借助ANSYS有限元分析软件对风力机叶片构建有限元模型，假设某风力机额定功率为600 kW，叶片设计风速13 m/s，风能利用系数0.4，风力机效率0.79，空气密度1.225 kg/m3。由公式（1）—（4）转化求叶轮直径（D），结果为43 m。根据风力机类型、叶片大小等参数，最终确定尖速比为6。风力机叶片翼型整体式设计保证（图1），保证叶片结构简单。

建模过程中，以上述参数为依据，并借助SHELL99单元划分网格。其中，所选定单元的节点数量有8个，单个节点自由度有6个。考虑到叶片结构分层性，通过构建有限元几何模型直观呈现叶片应力信息。以叶片简化设计为原则，保证风力机减负运行，针对叶片主梁结构夹芯处理，其中芯料采用轻木和PVC，实现降本、提质、减重、高强。

4 风力机叶片载荷及强度分析

4.1 叶片载荷

风力机叶片承受空气动力、离心力及重力，分别在3种力的作用下，使叶片承受弯曲与扭转、拉伸、拉压。对于空气动力载荷，需掌握叶片平面内（外）单位长度受力与叶片半径的关系情况：轮毂周围风力机叶片单位长度的平面外空气载荷与叶片半径大小呈正比例相关，考虑到叶尖损耗的存在，随着叶片运行时间的延长，则叶尖损耗加剧，一般而言，20 m半径单位长度的平面外空气载荷会逐渐减小。风轮平面内空气载荷在叶片半径周围分布较均匀，不会因半径增加而加大。对于离心力载荷，叶片离心力拉力影响因素主要有2个，分别是轮毂附近叶素微元质量、微元距离轮毂，确切而言，受微元线速度影响，拉力随着叶片径向延长而增大;受叶素微元质量影响下，拉力随着叶片径向延长而减小。对于重力载荷，来自重力的剪力、压力受叶素微元质量影响，主要呈递减趋势。

4.2 叶片强度

借助有限元模型分析风力机叶片强度，对此明确边界条件，将叶片简化为悬臂梁，叶片根部指围绕根部截面完全约束。接下来分析有限元数值，围绕单个叶片模拟，针对微元的空气动力、离心力、重力映射到模型节点，为叶片应力分析做准备，真正掌握叶片强度。随着叶片运行，记录运转方向的变形位移情况，并重点标记，相对而言，叶尖位置的变形、位置幅度较大，叶根处变形、位移幅度相对较小，运转及承载保持同向，变形及位移最大。风力机叶片的材料为玻璃纤维/环氧，基于各向异性表现，所以对叶片强度校核，全面掌握层合板结构状态，真实得知叶片应力情况。风力机叶片蒙皮结构为3层合板结构，基于Hill-蔡强度理论获取材料的强度校核数值，将其与1对比，如果数值小于1，说明叶片强度处于安全状态。强度校核结果显示，第一n8RUFP5Kc5tqP57AIvHZ7bHzdzHk7YNxBbZTFKD+4dA=层合板结构的强度校核数值为0.368 4，第二层和第三层的强度校核数值分别是0.425 6和0.826 5，说明三层合板结构安全，风机叶片未破坏。

从图1内容可知，层板铺设纤维材料的颜色发生变化，颜色渐变的过程，即层板强度增强的过程。

5 基于Monte Carlo的风力机叶片可靠性分析

5.1 需求分析

叶片在风力机建造中的占比达到18%左右，叶片质量关乎到风力机运行效果。由于风力机运行环境恶劣，意味着叶片运行期间承受较多载荷，一旦载荷超过叶片承受范围，极易导致风力机出现故障，因风力机停运造成严重的经济损失[5]。基于此，要对叶片可靠性展开分析。在需求导向下，合理选择叶片可靠性分析方法——Monte Carlo法，这一方法在传统计算方法的基础上升级而来，满足高维计算、便捷计算的需求。如今Monte Carlo法细分多种，其中，子集模拟法具有误差小、效率高、精度高、适用性强的优点，将其用于风力机叶片可靠性分析具有可行性。

5.2 翼型参数

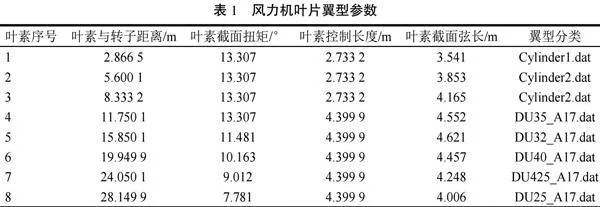
风力机叶片翼型的参数见表1，取1—8叶素序号。

叶片距根部约18%处达到最大弦长4.5 m，转子高度处平均额定风速为11.14 m/s，额定转速为12.09 rpm，风机的切入风速2.8 m/s，切出风速为23.9 m/s。

风力机翼型叶片在工作中一直处于转动状态，考虑到失速现象的存在，针对翼型升力系数、阻力系数修正，获得相对真实的翼型启动特性，为叶片可靠性分析做准备。建模分析过程中，针对叶片根部弯矩重点分析，目的是减少计算量、缩短计算时间，基于梁单元有限元模型获知叶片叶素的气动力，并显现于模型节点，具体掌握弯矩情况，针对叶片根部进行加固处理，保证叶片可靠性。

5.3 环境模拟

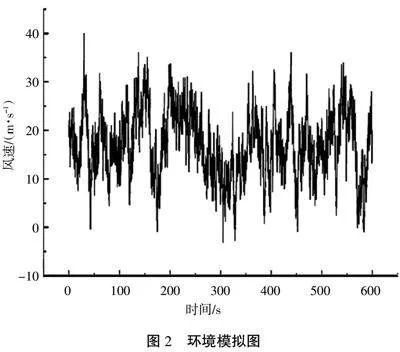
要想掌握风力机叶片的工作状态和强度情况，应首先模拟风场环境，根据风的形成原理，以及脉动风特征、参数，计算得知风载荷。风场环境模拟的过程中，选择谐波合成法，充分利用计算机快速计算、准确计算的优势完成模拟，顺风向风速与时间的关系情况如图2所示。模拟过程中，每间隔10 min对不同叶片方向进行风速记录，如果实际运行时间为580 s，前1 min排除瞬态响应的干扰，后520 s为采样时间，时间步长0.1 s。

5.4 Monte Carlo——子集模拟

Monte Carlo用于分析风力机叶片强度可靠性，随着叶片强度要求、可靠度要求提高，加之，风力机叶片失效概率低，Monte Carlo中子集模拟方法更具适用性。下面围绕子集模拟的应用原理、应用过程、计算分析具体探究。

5.4.1 应用原理

子集模拟是围绕每一阶段条件失效事件来代表最终小概率失效事件。实践过程中，基于马尔科夫链原理形成达标的新样本，并构建真实样本空间，面向失效概率空间高效计算、高效模拟。

5.4.2 应用过程

第一，确定建议概率密度函数。基于高斯概率分布函数，以及0～2π随机相位角序列形成新随机相位角序列，根据平稳随机过程模拟结果得知高斯分布标准差值。第二，先后进行Monte Carlo计算、生成N个马尔科夫链样本、所要求失效概率达标。上述是通过马尔科夫链蒙特卡罗法产生符合条件的样本的过程。

5.4.3 计算分析

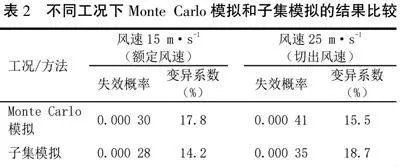
经工况模拟求得计算结果，工况一：风速15 m/s（额定风速）;工况二：风速25 m/s（切出风速）。分别进行Monte Carlo模拟（数据集10万个）和子集模拟（数据集1 000个）。Monte Carlo模拟需CJpPMAE9YPPb86SMslLRuA==要的样本数目较多，不同风速下的叶片失效概率、变异系数存在差异，风速15 m/s时，失效概率为0.000 30，变异系数为17.8%;风速25 m/s时，失效概率为0.000 41，变异系数为15.5%。子集模拟所需的样本数目较少，风速15 m/s时，失效概率为0.000 28，变异系数为14.2%;风速25 m/s时，失效概率为0.000 35，变异系数为18.7%。见表2。

比较发现，子集模拟的计算结果相对较小，风速15m/s时，失效概率为0.000 28，小于Monte Carlo模拟失效概率的0.000 30;风速25 m/s时，失效概率为0.000 35，小于Monte Carlo模拟失效概率的0.000 41。子集模拟在额定风速下变异系数14.2%小于Monte Carlo模拟变异系数17.8%，说明子集模拟计算精度较高。综合来看，子集模拟的样本量较少，且失效概率偏低，计算精度偏高，适用于风力机叶片强度可靠性分析，真实反映叶片工作状态，为叶片高强度、可靠性工作提供依据，实现风力机的常态运行。

6 结论

综上所述，风力机在风能向机械能转化方面发挥重要作用，风力机叶片是重要部件，其强度及可靠性影响风力机工作效率。通过Monte Carlo中的子集模拟法展开分析，发现额定风速工况下叶片失效概率偏低，且精度较高，能够以安全状态服务于风力机运行。

参考文献：

[1] 鞠浩，王旭东，陆佳红.神经网络正逆预测结合的风力机叶片强度可靠性研究[J].太阳能学报，2024，45（1）：291-298.

[2] 潘月月，李正农，张雨坤，等.基于实测风场的沿海风力机叶片流固耦合特性分析[J].太阳能学报，2023，44（12）：330-340.

[3] 赵清鑫，张兰挺.基于径向基神经网络的风力机叶片铺层优化[J].太阳能学报，2020，41（4）：229-234.

[4] 刁晓航，孙鹏文，马志坤，等.基于相变量的风力机叶片宏观拓扑优化设计[J].太阳能学报，2023，44（3）：198-203.

[5] 马航，毕俊喜，葛新宇，等.基于优化等寿命疲劳极限模型的风力机叶片寿命预测[J].太阳能学报，2023（10）：362-369.

基金项目：自治区直属高校基本科研业务费项目（JY20220305）;内蒙古自治区研究生科研创新项目（S20231130Z）;内蒙古科技计划项目（2022YFHH0055）

第一作者简介：王国富（1996-），男，硕士研究生。研究方向为复杂系统的可靠性。

*通信作者：毕俊喜（1974-），男，工学博士，教授，博士研究生导师。研究方向为复杂机电装备可靠性设计，制造、优化与控制。