基于神经网络与早至波的波方程反演

摘 要：针对传统波方程全波形反演步骤繁琐、计算量大和难度高等问题，提出一种基于全连接神经网络的早至波反演方法。实验结果表明，所提方法在早至波反演中交并比IoU（Intersection over Union）和平均精度均值mAP（mean Average Precision）分别达到74.01%和73.72%，可对速度模型进行有效重构。

关键词：波方程;早至波;神经网络;反演;交并比;平均精度均值

中图分类号：P631.4 文献标志码：A 文章编号：2095-2945（2024）30-0040-04

Abstract： Aiming at the problems of tedious steps， large amount of calculation and high difficulty in the full waveform inversion of traditional wave equation， a method for early-arrival wave inversion based on fully connected neural network is proposed. Experimental results show that the proposed method achieves 74.01% and 73.72% in the Intersection over Union（IoU） and mean Average Precision（mAP） of early-arrival wave inversion， which can effectively reconstruct the velocity model.

Keywords： wave equation; early arrival wave; neural network; inversion; Intersection over Urion; mean Average Precision

波方程主要描述自然界中的各种波动现象，求解一维波动方程的一般步骤是将其转化为一个简单的常微分方程或特殊的偏微分方程，然后通过求解该方程得到波动解析表达式。我们通过有限差分法求解以下波动方程[1]进行数值正演得到仿真波形数据集

▽P=-ρ

P=-ρc2▽u+Src（z，t） ， （1）

式中：z代表竖直方向的一维空间变量，t为时间项，P=P（z，t）为压强，作为常规空间梯度算子，u（z，t）代表竖直方向上的位移，ρ=ρ（z）为压强场密度分布，c=c（z）代表速度场，Src代表激发振动源项。

相较于正演，传统波方程反演的具体公式较为复杂，其本质框架是对以下残差平方和目标函数J的优化[2]

J=||dcalc-dobs||2 ， （2）

式中：dcalc代表通过反演计算得到的速度场数据，dobs代表原始速度场数据。搭建神经网络实现反演，意义在于使用神经网络去替代反演的过程，减少计算难度和时间。

1 方法

训练神经网络反演波方程一般根据早至波或初至走时，张利振等[3]提出的根据初至走时反演地层速度求解非线性地震走时问题以及Tarantola[4]提出的基于最小二乘法的全波形反演理论对波形反演起到了很大的推进作用，通过早至波进行反演也已经拥有了一定研究基础[5]。甚至也有相关研究[6]将早至波和初至走时联合反演。本文将利用早至波信息，完成基于早至波的波形反演。

近年来，深度学习在图像识别、语音处理等领域得到成功应用，为地震速度建模提供了新的方法[7-11]，例如U-Net神经网络、生成对抗神经网络和全卷积神经网络等都对该领域的研究提供便利。然而，当前可获取地震数据集较少，构建丰富且具有复杂特征的地震速度模型是当前深度学习速度建模的一大挑战。本文使用已搭建好的地震波仿真器依据一定的速度场计算得出地震早至波的早至压强，避免真实数据中噪声对神经网络训练的干扰，使训练更加理想化。

神经网络的具体优化方式为反向传播，是训练神经网络最有效且最常用的方法[12-14]：训练过程中神经网络的输出结果与实际结果会产生误差，计算过程输出与实际输出之间的误差，并将该误差从输出层向隐藏层直至输入层反向传播[15]

wl→wl-η∑x δl（al-1）T

bl→bl-η∑x δl， （3）

式中：wl表示第l层权重，al-1表示第l-1层输出，δl表示第l层误差，bl表示第l层偏置，η表示学习率，“→”表示对内部参数的更新。

本文计算不同速度场的波方程得出纵深-时间的时空压强场数组，对于速度场而言：由长度为2 000 ft的纵深上的速度值构成速度场;对于压强场而言：每一列代表纵轴上某一个接收器在不同时间上的压强大小，共有30列，每一行代表某个时间点上不同接收点处的压强大小，根据波传导到最深处的时间行数会有所变化，约在1 000行以内，且早至拾取完毕的时刻也会根据速度场的变化而变化，假定每0.01 s进行一次压强快照，接收点获取一次压强值。

神经网络模型以地震早至波的早至压强作为输入标签，速度场作为输出标签，通过两层隐藏层将地震数据由（z，t）域映射到速度模型（z，c）域，并在训练过程中不断更新隐藏层的权重w和偏置b，以达到使反演速度场贴近于真实速度场的目的。该过程可以用如下公式表示

θ（w，b）=argmin[θ（d）-v] ， （4）

式中：θ表示神经网络计算，w表示神经网络训练过程中的权重，b表示神经网络训练过程中的偏置，d表示地震早至波数据，θ（d）表示预测速度场，v表示真实速度场。

使用网格搜索的方式进行超参数调优，在训练过程中不断优化得到适合该网络模型的超参数：学习率为0.01，迭代次数为256次，每批次加载64组数据。输入层神经元数量为30，代表由30个接收器接收到的早至波压强，两层隐藏神经元数量分别为300和1 000，输出层神经元数量为2 000，代表波传导的深度为2 000 ft。使用FCN神经网络处理回归问题最常用的ReLU函数作为激活函数，用于引入非线性因素，使得神经网络能够拟合复杂的非线性关系。损失函数则使用普适的均方差损失函数。

具体方法的流程如图1所示。

数据选取：计算不同速度场的波方程得出纵深-时间的时空数组，拾取每一列上的早至压强数据。

输入层：输入层神经元数量为30，代表由30个接收器接收到的早至波压强，将64批次的早至波向量构成的混淆矩阵作为神经网络的输入。

隐藏层：设置两层隐藏层神经元，数量分别为300和1 000，可以有效且平稳地从输入层30个神经元传播到输出层2 000个神经元。在训练过程中不断计算梯度和更新神经元层之间的偏置与权重，实现误差的反向传播。

输出层：输出层神经元数量为2 000，代表波传导的深度为2 000 ft，以64批次的真实速度场作为输出。

反演对比：将神经网络反演出的速度场与真实速度场进行对比，观察神经网络是否能准确反演波方程。

2 数据来源和选取

有限差分法有计算迅速、精度较高、易在计算机上实现的优点，故使用此方法求解波方程，对速度场进行正演，得到其数值解，使用传统STA/LTA方法拾取早至波压强，在理想的低信噪比环境下快速且简易[16]，最终将早至波压强场与真实速度场构成的数据对作为神经网络的训练标签，划分80%的训练标签用于训练，20%的训练标签用于测试。

神经网络的训练结果很大程度上依赖数据集规模，不合适的数据集往往会造成以下问题。

当数据量过多，模型可能会过度拟合训练数据，过度学习训练数据中的噪声和特定的样本特征，而忽略了一般化的模式。这导致模型在未见过的数据上表现不佳。

过少的数据集模型可能无法捕捉到数据的复杂结构和泛化模式，导致模型在训练数据和测试数据上都表现不佳，从而无法在真实反演中推广到新数据上。

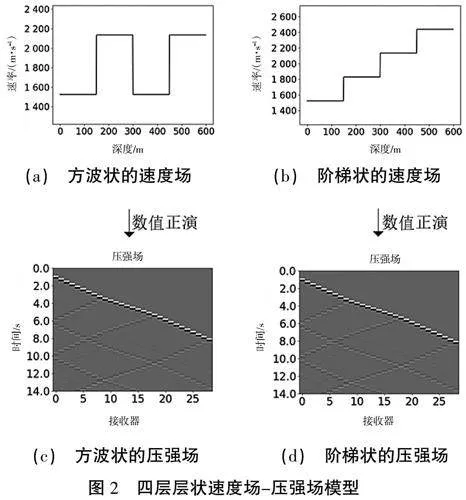
不合理的数据集需要更多的计算资源进行训练，包括更多的内存、更长的训练时间和更高的计算成本。本文通过多次实验，最终选定数据集大小为1 280组，其次限制所有类型速度场的范围为[1 219.2 m/s，2 743.2 m/s]，速度场层数为4层。本文仿真了上述速度场类型，在此基础上对速度场求解波方程的到压强场。图2展示了其中2种速度场类型对应的压强场的求取过程。

3 结果

3.1 神经网络训练结果与分析

如图3所示，可以看到通过输入早至波反演出速度场，将真实速度场与反演速度场进行对比，显示了该方法可以精细刻画层状速度场，整体而言较为接近真实速度场，反演效果较好，但加入小范围凹陷后，其并不能有效刻画凹陷处速度场，KnI/SPfLCXzvEwHxSknstA==对于凹陷处速度场反演并不够充分，精确度有待提高。

3.2 模型评估

使用常见回归模型评价指标，包括交并比IoU（Intersection over Union）、平均精度AP（Average Precision）和平均精度均值mAP（mean Average Precision）。这些指标统称为测试误差，是测试集的预测值和真实值的统计量通过多方位标准评估该神经网络的泛化能力和预测高效性。将速度场与x轴形成的区域视为待预测物体，可得出本模型训练集平均IoU约为0.98，测试集平均IoU约为0.74，故将IoU阈值设定为0.8，IoU≥0.8的测试用例视为正确预测，将模型转换为分类任务，画出精准率-召回率PR（Precision-Recall）曲线、计算方波状速度场和阶梯状速度场情况下的AP和总的mAP。

PR曲线与坐标轴围成的面积是用于评估分类模型优劣的常用方法，图4表明本模型PR曲线较为理想，且表1中2种分类AP值波动不大且得出平均值mAP符合预期，这说明本文神经网络具有一定泛化能力，在测试范围内预测精确性较高。

但是本模型依然存在一定的局限性：在选取数据集时，选定速度场为层状速度场，且规定速度场的层数和范围，这使本神经网络反演其他类型的速度场时效果不佳。其次，对于现实世界中的地震波而言，速度场不可避免会存在一定塌陷[17]，即小范围孤立异常体，在后续神经网络的优化中，可针对这一问题进行进一步研究。

4 结论

本文通过神经网络研究了面向早至波的波方程反演方法。神经网络训练结果显示，早至波神经网络反演方法可以精确地刻画层状速度场，具有一定反演精度。随机训练过程对相同层状速度模型的建模结果显示，模型预测精度不具有随机性，是比较稳定的，并且花费较少的时间成本和运算成本[18]。但在现实世界的地震波或者其他应用场景中，需要获取足够数量且具有不同特征的数据集，以提高神经网络的的泛化能力和应用范围。

参考文献：

[1] 斯小琴，陈大伟.一维波动方程的计算模拟[J].淮北师范大学学报（自然科学版），2022，43（3）：22-25.

[2] 崔丛越，王彦宾.一维速度结构的地震波全波形反演理论测试[J].北京大学学报自然科学版，2019，55（2）：246-252.

[3] 张利振，孙成禹，王志农，等.面波信息约束的初至波走时层析反演方法[J].物探与化探，2023，47（5）：1198-1205.

[4] TARANTOLA A. Inversion seismi reflection data in the acoustic approximation[J].Geophysics，1984，49（8）：1259-1266.

[5] 孙明皓，余瀚，陈雨青，等.基于U形多层感知机网络的地震波初至拾取与反演[J/OL].计算机应用：1-11[2024-04-15].http：//kns.cnki.net/kcms/detail/51.1307.TP.20230828.1444.011.html.

[6] 许祥，邹志辉，韩明亮，等.联合地震初至走时与早至波形的深度学习速度建模[J].地球物理学报，2023，66（12）：5107-5122.

[7] 许祥，邹志辉.地震早至波深度学习速度建模[C]//中国地球物理学会油气地球物理专业委员会.第五届油气地球物理学术年会论文集.中国海洋大学海洋地球科学学院海底科学与探测技术教育部重点实验室深海圈层与地球系统教育部前沿科学中心;青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室，2023：5.

[8] ARAYA-POLO M， JENNINGS J， ADLER A， et al. Deep-learning tomography[J].The Leading Edge，2018，37（1）：58-66.

[9] MOSSER L， KIMMAN W， DRAMSCH J， et al. Rapid seismic domain transfer： Seismic velocity inversion and modeling using deep generative neural networks[C]//80th eage conference and exhibition. EAGE Publications BV，2018：1-5.

[10] YANG F， MA J. Deep-learning inversion： a next generation seismic velocity-model building method[J]. Geophysics，2019，84（4）：583-599.

[11] 廖成旺，庞聪，江勇，等.基于多层全连接神经网络的6C地震波极化向量识别研究[J/OL].大地测量与地球动力学，1-11[2024-02-05].https：//doi.org/10.14075/j.jgg.2023.06.158.

[12] 马雄，申天赐，李国发，等.重构震源振幅谱一致性的吸收参数反演方法[J].石油地球物理勘探，2024，59（1）：122-132.

[13] 胡豹，高永卫，昔华倩.基于误差反向传播神经网络的机弹分离轨迹预测研究[J].气动研究与试验，2024，2（2）：59-65.

[14] 刘浩民，杨洪才，刘战，等.基于粒子群优化算法的电弧增材制造焊道尺寸反向传播神经网络预测模型[J].机械工程材料，2024，48（2）：97-102.

[15] 张驰，郭媛，黎明.人工神经网络模型发展及应用综述[J].计算机工程与应用，2021，57（11）：57-69.

[16] 谭玉阳，于静，冯刚，等.微地震事件初至拾取SLPEA算法[J].地球物理学报，2016，59（1）：185-196.

[17] 赵俐红，刘欣悦，支鹏遥，等.南海东北陆缘的地壳速度结构及其构造意义：来自广角地震剖面的约束[J].地质学报，2023， 97（6）：1766-1779.

[18] 马月宁，郑晶. 基于深度神经网络的地震速度模型反演[C]//中国地球科学联合学术年会.2021年中国地球科学联合学术年会论文集（三十六）-专题一百零六 地球科学大数据与人工智能、专题一百零七 地球生物学与天体生物学、专题一百零八 古脊椎动物学最新进展.北京伯通电子出版社，2021：4.

基金项目：江苏省大学生创新创业训练计划项目（202310293095Y，202210293098Y）

*通信作者：余瀚（1984-），男，博士，副教授。研究方向为反演成像、机器学习。