有关两类特殊三角形问题的解法

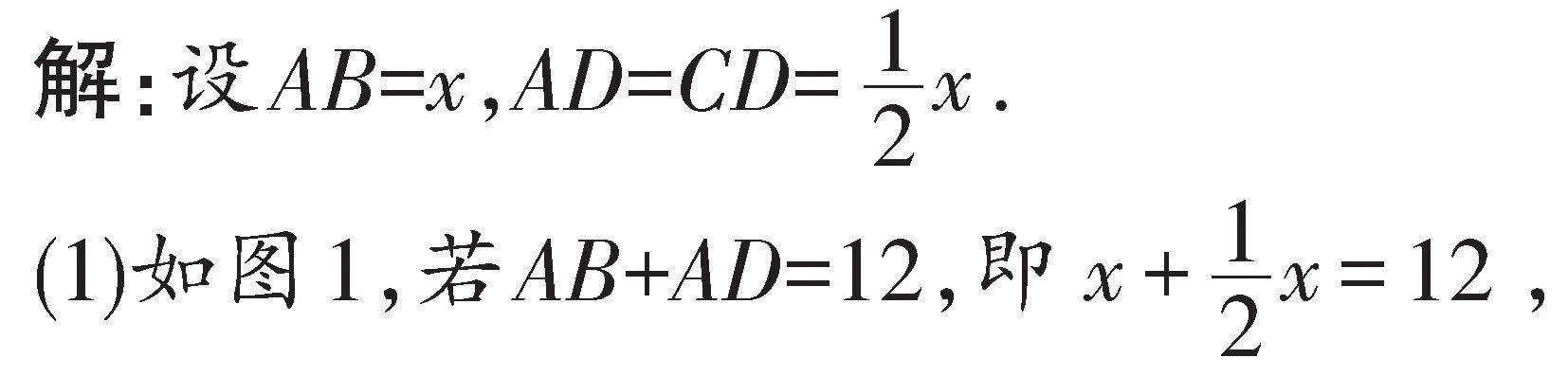
三角形按边分类主要可以分为三边不相等的三角形、等腰三角形、等边三角形.其中等腰三角形、等边三角形比较特殊，它们具有独特的性质，还有一些相关的重要定理.有关等腰三角形、等边三角形的问题比较常见，下面主要探讨一下这两类问题的解法.

一、等腰三角形问题

有两条边相等的三角形叫做等腰三角形，相等的两边都叫做腰.常见的等腰三角形问题有：（1）求等腰三角形的边长；（2）求等腰三角形的一个内角；（3）判断三角形的三边关系能否构成等腰三角形；（4）求等腰三角形的周长；（5）求等腰三角形的面积.在解答等腰三角形问题时，要先明确三角形的哪条边是底边，哪两条边为腰，然后根据三角形的内角和定理以及等腰三角形的性质来解题.若等腰三角形的顶角、底角是未知的或不确定的，腰或底是不确定的，则需运用分类讨论思想，讨论三角形的三条边、角以及三角形的存在性.

①当腰长为2时，三角形的三边分别为2、2、3，能组成三角形，则三角形的周长为2+ 2+3=7；

②当底边长为2时，三角形的三边分别为2、3、3，能组成三角形，三角形的周长为2+ 3+3=8，

所以该等腰三角形的周长为7或8.故本题选D项.

说明：我们HSgMObwfQDOOOzX1Y492NwvvsqIneLCbjMi79vnuVGI=需先根据非负数的性质列出方程组，通过解方程组求出a、b的值；再将a

的值视为腰长或底边长两种情况来进行讨论、求解.

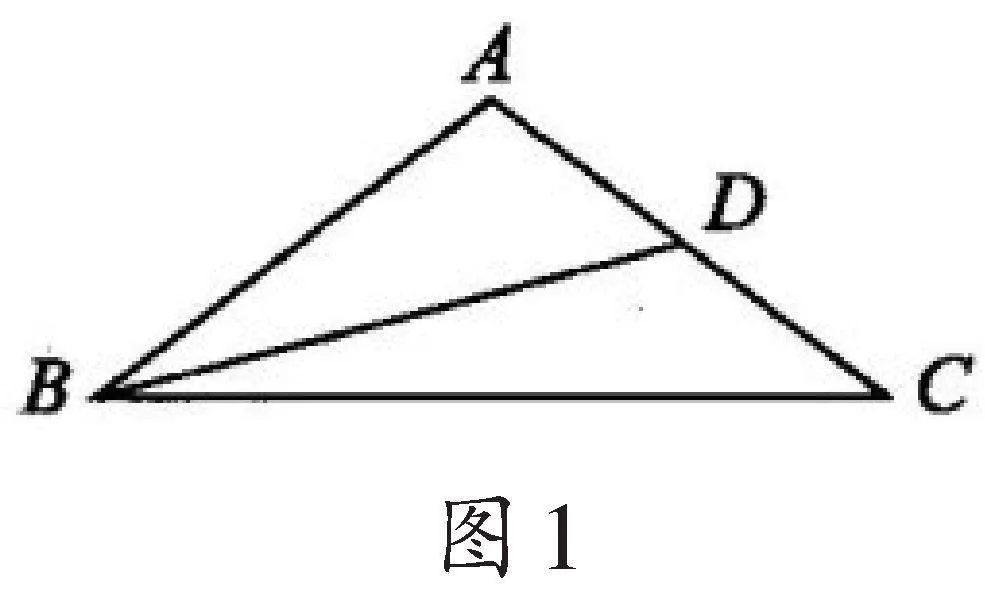
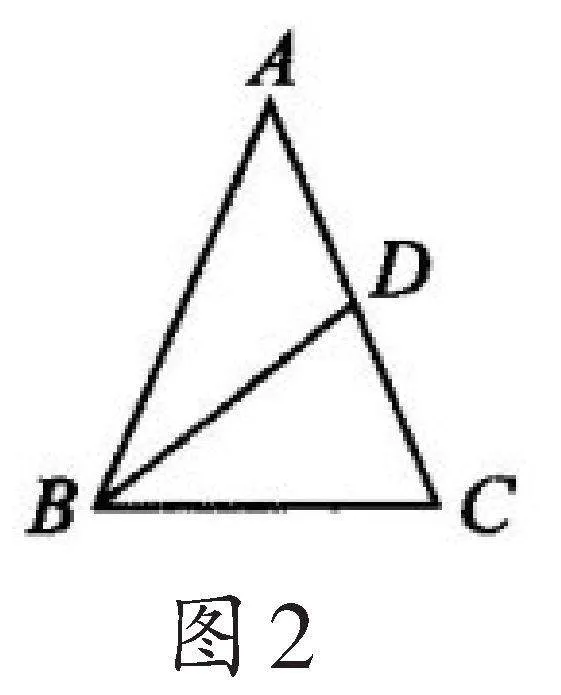
例2在△ABC中，AB=AC，AC边上的中线BD把△ABC的周长分为12cm和15cm两部分，求三角形的各边长.

解得x=8，

即AB=AC=8，则CD=4.故BC=15-4=11.

此时AB+AC>BC，所以三角形的三边长为8，8，11.

解得x=10.

即AB=AC=10，则CD=5.故BC=12-5=7.

此时AB+AC>BC，所以三角形的三边长为10，10，7.

综上所述，此三角形的三边长分别为8， 8，11或10，10，7.

说明：BD把△ABC的周长分为12cm和15cm两部分，哪部分是12cm，哪部分是15cm， 需进行分类讨论.

二、等边三角形问题

三边都相等的三角形为等边三角形.等边三角形是三边都相等的特殊等腰三角形，又叫正三角形.其三个内角都相等，都等于60°；三角形中所有边上的高、中线与所有角平分线都相等.常见的等边三角形问题主要有求等边三角形的边长、高线长、面积.解答等边三角形问题，需根据三角形的三角、三边

都相等的性质来求解.

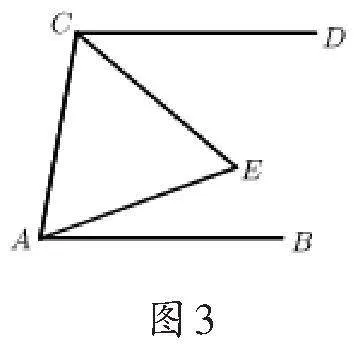
例3如图3，已知AB∥CD，△ACE为等边三角形，∠DCE=40°，则∠EAB等于（）.

A.40° B.30 C.20°D.15°

解：∵△ACE为等边三角形，

∴∠ECA=∠EAC=60°，

∵AB∥CD，∴∠DCA+∠BAC=180°，

∴∠DCE+∠ECA+∠EAC+∠EAB=180°，

∵∠DCE=40°，

∴40°+60°+60°+∠EAB=180°，

解得∠EAB=20°，∴本题选C项.

说明：先根据等边三角形的性质可得∠ECA=∠EAC=60°，再根据平行线的性质可得∠DCA+∠BAC=180°，然后根据角的和差关系建立关系式即可解题.

可见，解答等腰三角形问题和等边三角形问题，关键是要灵活运用这两种三角形的性质来建立边角关系.此外，还需要注意以下两点：（1）三角形的内角和为180°；（2）三角形任意两边的和大于第三边，三角形任意两边的差小于第三边.这是判断三条线段能否组成三角形的关键.