由一道题谈“三垂直全等模型”在解题中的应用

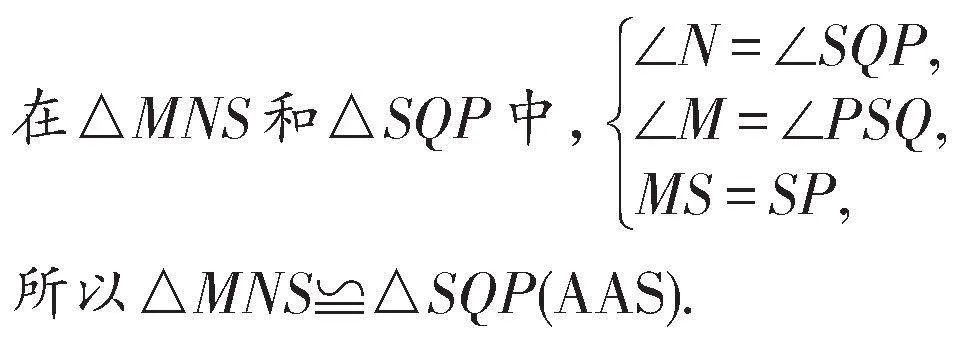
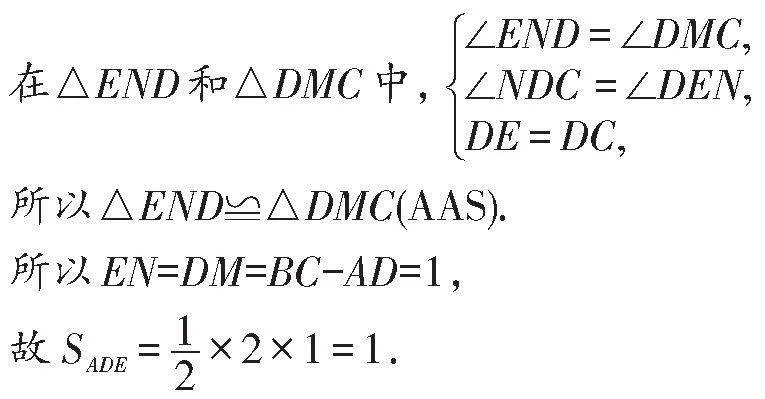
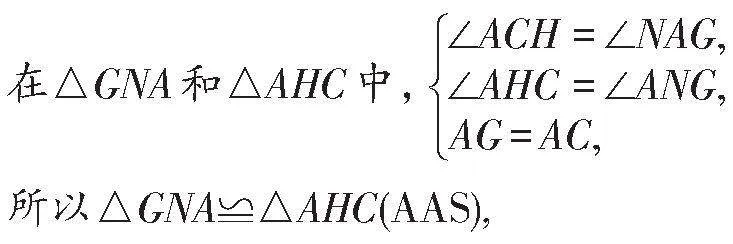
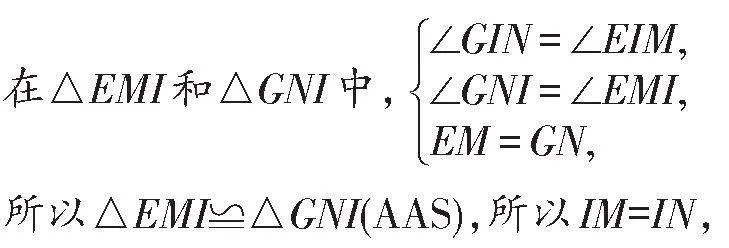
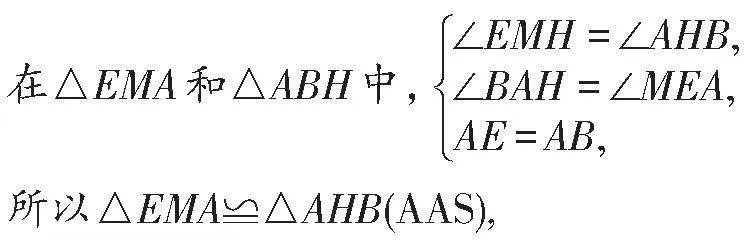
在解几何题时，几何模型能够引领我们找到解题的思路，是解答几何问题的利器.本文对苏科版八年级上册教材第35页的一道习题所蕴含的思想方法进行了提炼，深入解读了“三垂直全等模型”，并结合实例探究了该模型在解题中的具体应用方法.希望同学们今后在解题中能灵活运用该模型解题.

苏科版八年级上册教材第35页第5题：

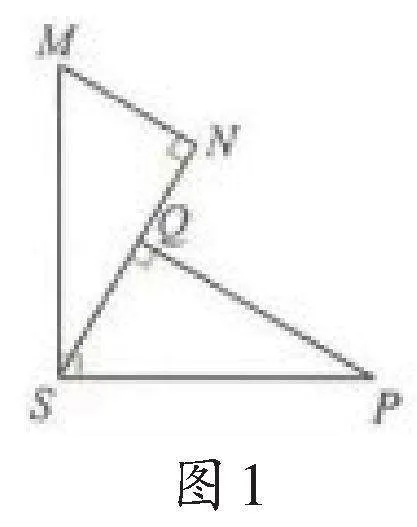
如图1，已知MS⊥PS，MN⊥SN，PQ⊥SN，垂足分别为S，N，Q，且MS=PS.求证：△MNS≌△SQP.

证明：因为MS⊥PS，MN⊥SN，PQ⊥SN，

所以∠MSP=∠N=∠SQP=90°，

所以∠M+∠MSN=∠MSN+∠PSQ=90°，

所以∠M=∠PSQ.

所以△MNS≌△SQP（AAS）.

说明：我们直接根据角之间的互余关系证明∠M=∠PSQ，即可根据三角形全等的判定定理AAS证明△MNS≌△SQP.

一、对“三垂直全等模型”的解读

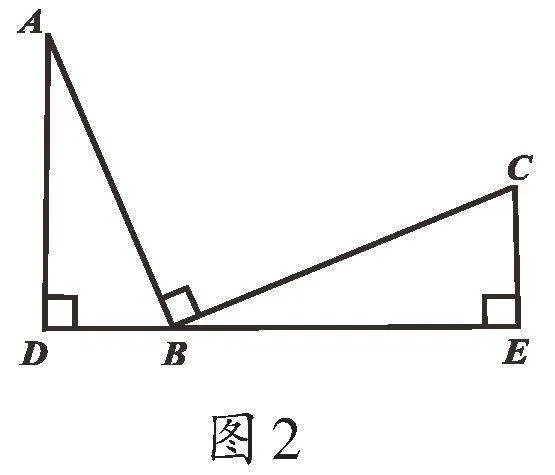
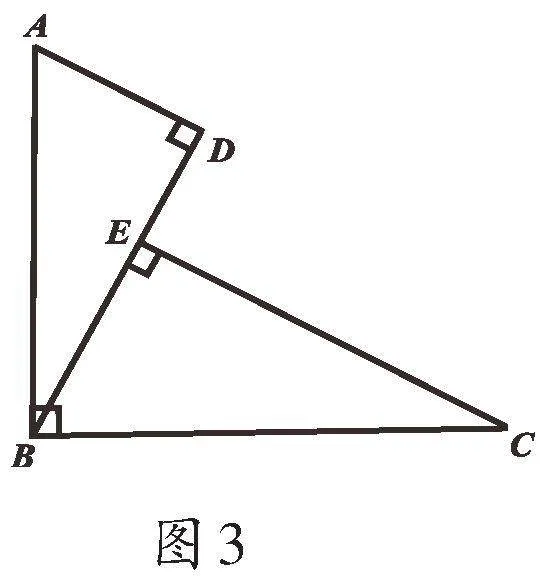
上述习题中出现三组垂直关系：MS⊥PS，MN⊥SN，PQ⊥SN，且两个直角三角形全等，我们称这种模型为“三垂直全等模型”.在解题中，我们经常会遇到这种模型，如图2、3，∠ABC=∠ADB=∠BEC=90°，直角顶点D、B、E三点在同一条直线上，且BC=AC，这样的模型都可以称为“三垂直全等模型”.

在该模型中，△ABC为等腰直角三角形，从两个底角顶点向过直角顶点B的一条直线作垂线段，即可得到两个全等直角三角形△ADB、△BEC，由此可得到有关边的等量关系，即：AD=BE，BD=CE，DE=BD+BE（图2）， DE=BD-BE（图3）.

二、“三垂直全等模型”在解题中的应用

尽管“三垂直全等模型”在几何图形中有较高的识别度，但有的题目综合性强，图形复杂，涉及的知识点比较丰富，如函数、直角坐标系，三角形、四边形等，此时要构造“三垂直全等模型”就要抓住几个关键点：三个直角、两个相邻的锐角互余、一个等腰直角三角形， 然后据此建立边角关系来证明两个三角形全等，从而获得更多的边角等量关系.如果题目所提供的图形中隐藏了部分直角，模型呈现不完整，还需要添补辅助线补全模型.

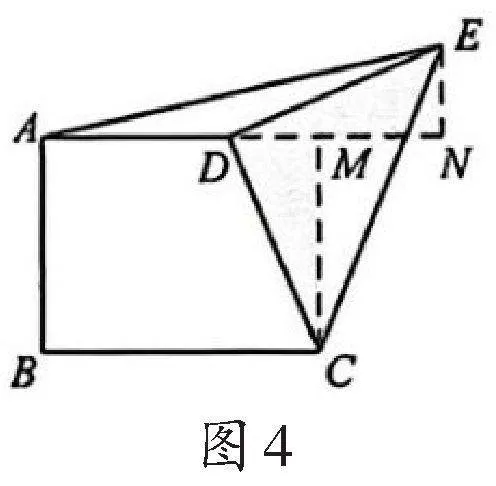
例1如图4，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=2，BC=3，将腰CD以D为中心逆时针旋转90°至ED，连接AE、CE，求

△ADE的面积.

解：如图4，过点E作EN⊥AD，交AD的延长线于点N，过点C作CM⊥DN，交DN于M点.

因为腰CD以D为中心逆时针旋转90°至ED，

所以∠EDC=90°，

因为EN⊥AD，CM⊥DN，

所以∠END=∠DMC=90°，

所以∠DEN+∠NDE=∠NDE+∠NDC=90°，

所以∠NDC=∠DEN.

所以△END≌△DMC（AAS）.

所以EN=DM=BC-AD=1，

说明：本题中ED⊥DC，作辅助线EN⊥AD、CM⊥DN，即可构造出“三垂直全等模型”，然后根据角之间的互余关系、等腰直角三角形的性质建立等量关系式，即可根据三角形全等的判定定理AAS证明△END、△DMC全等，从而获得问题的答案.

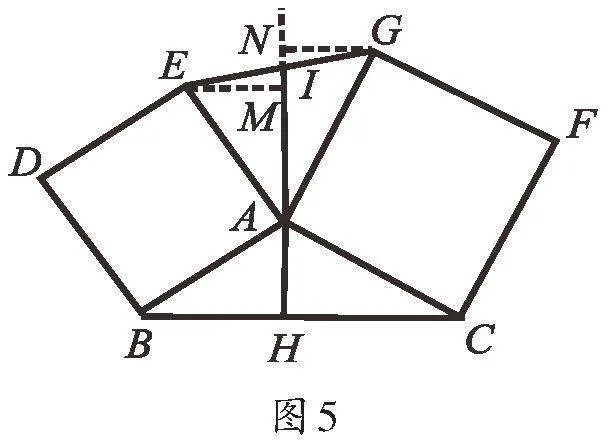
例2如图5，向△ABC的外侧作正方形ABDE、正方形ACFG，过点A作AH⊥BC于H，AH的反向延长线与EG交于点I.求证：BC=2AI.

证明：如图5，过E作EM⊥HI于M，GN⊥HI的延长线于N，所以∠EMI=∠GNI=90°.

因为ABDE为正方形，

所以∠EAB=90°，AE=AB，

因为AH⊥BC，所以∠AHB=90°

所以∠EAM+∠BAH=∠EAM+∠MEA=90°，

所以∠BAH=∠MEA.

所以△EMA≌△AHB（AAS），

则AM=BH，EM=AH.

因为ACFG为正方形，

所以∠GAC=90°，AG=AC，

因为AH⊥BC，所以∠AHC=90°

所以∠HAC+∠ACH=∠HAC+∠NAG=90°，

所以∠ACH=∠NAG.

所以△GNA≌△AHC（AAS），

则AN=CH，AH=GN.

所以△EMI≌△GNI（AAS），所以IM=IN，

所以BC=BH+CH=AM+AN=AM+AI+IN=AM+IM+AI=AI+AI=2AI.

说明：解答本题，需根据正方形的性质找出直角、等边、等角，然后作出垂线，构造出“三垂直全等模型”，据此找到两组全等三角形：△EMA≌△AHB、△GNA≌△AHC，从而得到一些边角的等量关系；再根据△EMI≌△GNI建立边之间的等量关系，进而证明BC=2AI.

虽然以上两例涉及到的知识点有所不同，例1涉及了直角梯形和旋转相关的知识，例2是以正方形为背景的，但解题的核心都是运用建模思想，构造了“三垂直全等模型”.初中几何涉及了众多的模型，对于一些常见的几何模型，同学们要对其进行深入的探究，总结出规律，达到“通一题会一类题”的效果，从而掌握问题的本质，提高解题能力.