谈谈与双角平分线模型有关的结论的应用

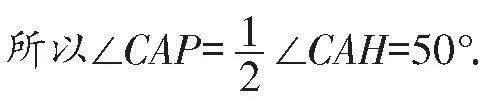
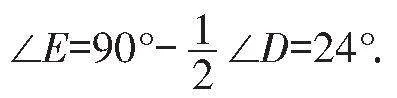
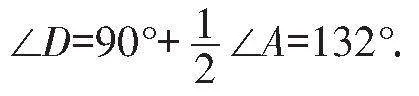
角平分线以其独特的性质在三角形中占有重要的地位.围绕三角形的内角和外角的角平分线建构的几何模型对解答相关的几何问题有着重要的意义.本文对三角形的双角平分线的经典模型的构造、论证进行了归纳与总结，并探讨了它们在解几何题中的一些应用.

一、双内角平分线模型

从这一结论可以看出，三角形中两内角平分线所成的角的大小仅与第三个内角的大小有关，与两内角无关.因此，只要第三个内角恒定不变，无论这两个内角如何变化，它们的角平分线所成的角的大小不变.抓住这一不变量往往能为我们顺利找到解答问题的突破口.

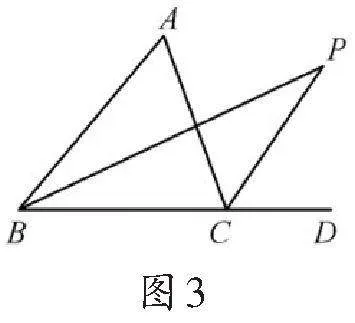
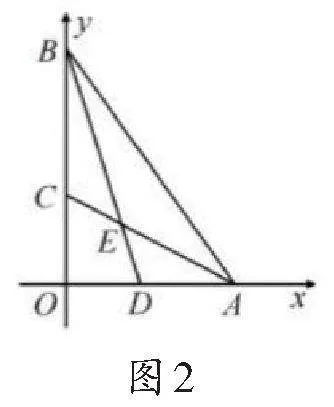
例1在平面直角坐标系中，△AOB的顶点A、B分别为x轴，y轴上的动点，点E是△ABO的两条角平分线的交点，如图2，在点A、B的运动过程中，∠BEC的大小是否发生变化？请给予判断，并说明理由.

解：∠BEC的大小不会发生变化，理由如下：

在∠AOB中，因为BE，AE分别为∠ABO和∠OAB平分线，

所以∠BEC=180°-∠AEB=45°，

即∠BEC的大小不会发生变化，恒为45°.

评注：随着点A，B的运动变化，两个内角∠ABO，∠BAO的度数也会发生改变，但是∠AOB=904701c1f14da6c6d9e9b319991cae6461cde43cd3cfe71b31224b6504e5bc3248°始终不变，而∠AEB的大小仅与∠AOB相关，所以∠AEB不会变化，从而判断∠BEC不变.解答这类动点问题时，以静制动，借助模型寻求图形运动变化中的变量与不变量的关系，才能找准切入点，明确解题思路.

二、内外角平分线模型

从这一结论可以看出，一个内角和一个外角平分线所形成的夹角的大小仅由第三个内角的大小决定，且仅为该角的一半.在解题中，我们要分清哪个角是由内外角平分线所构成的角，并与第三个内角建立对应关系是解题的关键.当题目所给条件不足时，需要添加辅助线让这一模型显性化.

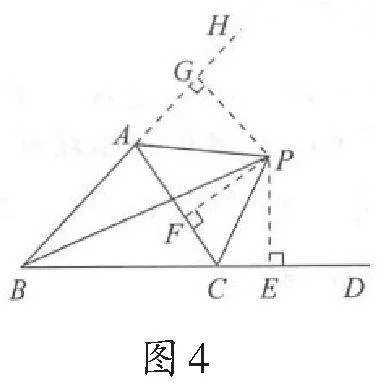
例2如图4，△ABC的外角∠ACD的平分线CP与内角∠ABC的平分线BP交于点P，若∠BPC=40°，则∠CAP=（ ）.

解：本题中的内角∠ABC的平分线与外角∠ACD的平分线交于点P，且∠BPC=40°，

由内外角平分线模型可知，∠BAC=80°，

所以∠BAC的外角为180°-80°=100°.

如图4，延长BA，过点P分别作PE⊥BD于点E，作PF⊥AC于点F，作PG⊥BA于点G，

因为BP平分∠ABC，所以PE=PG，

同理PF=PE，PG=PF，

所以AP为∠CAH的角平分线，

评注：本题中的内外角平分线模型是显而易见的.但是要求∠CAP，需要进一步证明AP是外角平分线，所以通过作垂线，利用角平分线的判定定理予以证明.由本题可以得到的结论是三角形的一条内角平分线与其他两个角的外角平分线交于一点.

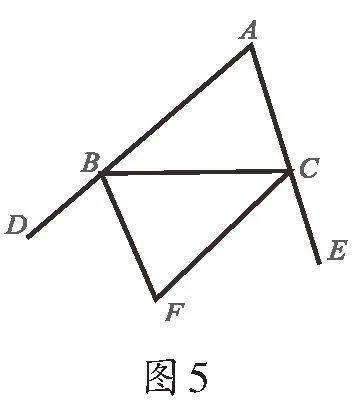
三、双外角平分线模型

由这一结论可知，两外角平分线所构成的角仅与第三个内角的大小有关.当题中出现这一模型时充分利用这一结论，可以省去利用内外角定理进行推导的过程，起到事半功倍的效果.

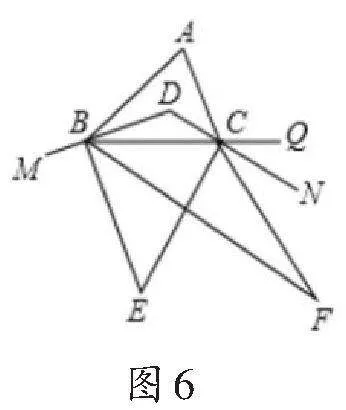
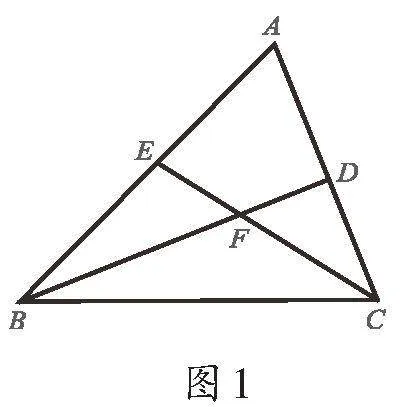
例3如图6，在△ABC中，∠A=84°，BD、CD分别平分∠ABC、∠ACB，M，N，Q分别在DB、DC、BC的延长线上，BE、CE分别平分∠MBC、∠BCN，BF、CF 分别平分∠EBC，∠ECQ，则∠F=________.

解析：在△ABC中，BD、CD为∠ABC、∠ACB的平分线，

由双内角平分线模型可知，

在△BCD中，BE、CE分别平分∠MBC、∠BCN，

由双外角平分线模型可知，

在△BCE中，BF、CF分别平分∠EBC，∠ECQ，

评注：本题构图复杂，多次出现角平分线，需要明确这些角平分线与哪个三角形有关，且是双内角平分线还是双外角平分线，或是一内一外角平分线.如果直接利用三角形内角和定理和外角性质推导计算较为繁琐，那么，通过三次运用角平分线模型则能轻松求解.

总之，围绕三角形的内外角平分线所建构的几何模型，是对双角平分线所构成的角与三角形的另一个内角之间关系的探索.无论三角形的形状如何变化，它们之间的关系始终确定不变.因此，同学们只要把握模型的实质，抓住基本特征，就能在解题中运用自如.