无人机航迹规划算法研究进展

摘 要：目前，无人机技术的发展已取得了明显的突破，无人机的应用领域从军事扩展到了商业、科研、娱乐等多个领域。文章以无人机航迹规划算法为研究对象，首先，根据航迹规划算法的原理与特点，将其分为全局规划算法和局部规划算法两大类，其中全局规划算法又可分为图搜索算法和智能仿生算法。其次，对算法的原理、工作流程、优缺点进行了深入分析，并介绍了相应的改进方法，结合算法自身特点阐述其在相应领域的应用；最后，探讨上述算法在实际应用中的限制与挑战，并对未来航迹规划技术的发展趋势进行了展望，为无人机航迹规划算法的研究指出了方向。

关键词：无人机；航迹规划；全局规划算法；局部规划算法；图搜索算法；智能仿生算法

中图分类号：TP301；V279 文献标识码：A 文章编号：2096-4706（2024）17-0049-07

0 引 言

无人机航迹规划的优劣决定着无人机是否能实现自主飞行，并独立完成任务。航迹规划的本质是在满足任务要求的前提下寻找从起始点到目标点的最优航迹。在缉毒侦察、军事行动[1-2]等领域中，飞手操作无人机只能进行一些简单的避障操作，利用无人机进行动态瞄准等高难度操作则难以实现，若无人机可以实现自主飞行，将能够改善无人机在任务执行时遇到的一系列问题，同时还可节省人力资源。在满足任务需求的前提下，使得效率最大化的同时，将损耗降到最低，这其中飞行时间和距离往往被考虑为航迹优化过程中的关键因素，避免碰撞是该过程需要解决的关键问题。航迹规划算法的研究起源于复杂科学问题的求解，逐渐发展成为一门交叉科学，涵盖了计算机科学、人工智能、运筹学、控制理论等多个领域。随着计算能力和算法理论的发展，无人机航迹规划算法从最初的格点法、人工势场法到后来的启发式与进化算法，计算效率与航迹质量都得到了质的提升。本文对常见的航迹规划算法进行分类，探讨其基本原理、实现方式以及优缺点，最后对该领域的研究状态、挑战和未来趋势进行了探讨。

1 无人机航迹规划算法分类

算法是航迹规划的核心，目前有诸多方法对无人机航迹规划算法进行分类，其中最常见的是基于对环境信息的掌握程度进行的分类，分别为全局航迹规划算法与局部航迹规划算法。全局航迹规划算法需要掌握并根据环境地图的所有信息进行航迹规划，这将导致不能应对出现在环境中的未知障碍物；而局部航迹规划算法可以实时采集环境信息，根据已知的环境信息确定出所在位置及障碍物分布情况，从而进行航迹规划。

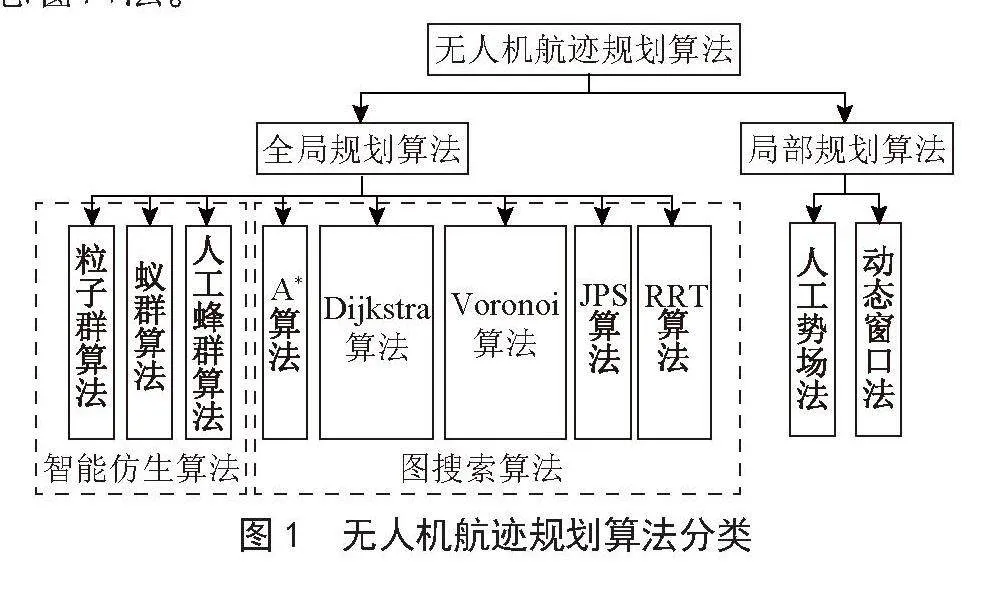
全局航迹规划算法可分为图搜索算法和智能仿生算法，如图1所示。图搜索算法主要包括A*算法、Dijkstra算法、Voronoi图法、JPS算法、RRT算法，智能仿生算法主要有粒子群算法、蚁群算法、人工蜂群算法。局部航迹规划算法主要包含人工势场法和动态窗口法。

2 图搜索算法

图搜索算法是一种基于图数据结构搜索航迹的算法。其基本思想是从某个节点出发，沿着边连接的其他节点，最后到达目标节点，节点表示在空间中的位置，边则代表位置之间的连接通路。在无人机航迹规划中，无人机所处的环境可以被建模为一个图形，图中的节点是无人机可能出现的飞行位置，边则代表无人机可以飞行的航迹，图搜索算法可以有效地找出从起点到终点的最优航迹。

Dijkstra算法不使用任何启发式信息，只是简单的探索所有航迹直到找到目标点，因此只适用于环境相对简单的场景。A*算法将Dijkstra算法确保最短航迹的特点与贪心算法的高效搜索相结合，通过启发式函数优化航迹，使得无人机能在复杂环境中快速找到目标点。Voronoi图法通过对空间的有效分割，为无人机提供了避免障碍物和处理开放空间的能力，这对于城市和崎岖地形的飞行尤为重要。JPS算法作为A*的一种优化，通过跳过不必要的节点来加快网格地图中的搜索速度，提高了在标准化环境中的航迹规划效率。而RRT算法以其随机化的探索方式，特别适合于复杂和动态变化的飞行环境，如林区或急剧变化的城市景观。

将这些算法综合应用于无人机航迹规划，可以实现一种既灵活又高效的航迹规划策略，能够在确保安全和效率的同时，优化航迹并缩短飞行时间。本章将着重介绍目前应用较多的A*算法和RRT算法。

2.1 A*算法

A*算法是1968年由Hart[3]提出的一种启发式搜索算法，常用于计算两点之间的最短航迹。该算法在搜索过程中引入了启发式函数，即预估从当前节点至目标节点的最小代价。通过这种方式，在搜索范围较大的情况下A*算法仍能保持较高的搜索效率。其基本原理是每次从待搜索的节点中选择一个“最有希望”（即预计总代价最小）的节点进行搜索，直到找到目标为止。这种算法的特点是它可以找到一条最短航迹（前提是启发式函数不大于实际代价）。

A*算法是一种很有效的寻路算法，它能保证在有解的情况下一定能找到最优解，为了进一步提高航迹搜索的方向性和减少无效探索，Chen等[4]通过比较当前节点到目标节点的航迹与最优直线航迹之间的角度，来判断节点是否有利于朝目标方向前进。并有针对性地设计了

新的评估函数H1（n）=H（n）-wcosθ，其中H（n）为以往的评估函数，w为一个权重参数。这个新评估函数减少了对无用节点的探索，提高了运行效率和航迹质量。

针对传统A*算法在无人机航迹规划中效率低下、航迹点过多且航迹转折频繁的问题，唐嘉宁等[5]引入了双向搜索机制，分别以起点和终点为对向搜索的起点，基于起点和终点所处的象限进行双向定向搜索，通过双向搜索获得的初始航迹进行平滑处理，以减少冗余航迹点和转折点。Zhang等[6]在此基础上提出了一种双向多层A*搜索方法，以提高搜索三维空间的效率。这种方法通过在起点和目的地之间同时进行正反向的搜索，并在两个OPEN列表的轨迹点相遇时停止搜索。通过在特定角度扇区内进行多层可变步长搜索的策略，以进一步提高搜索效率，并在雷达威胁较大时调整搜索步长，在保证了航迹全局优化的同时，确保了航迹的安全性。

2.2 RRT算法

RRT（快速随机探索树）算法是由LaValle[7]提出的一种航迹规划算法。该算法在无人机航迹规划中主要用于在未知环境中寻找从起点到终点的最优航迹，该算法适用于包含障碍物和差分运动约束的场景。然而，由于其搜索过程中的随机性，生成的航迹可能并非最优，而且可能存在大量冗余航点。针对这一问题，研究人员提出了例如调整步长或者结合启发式步长调整策略对初步生成的航迹进行修剪处理，以缩短航迹长度等多种改进策略来优化RRT算法。

顾子侣等[8]在随机树待扩展节点的选取上引入目标启发信息，在新节点生成和添加过程中融入无人机动力学约束，在确保生成航路符合实际飞行的可行性的基础上，针对突发威胁情况，提出一种动态扩展随机树方法，该方法可以对原有随机树进行剪枝和重构，以快速避开威胁并生成一条安全航路。

为了能让算法在有障碍物的环境中更高效地进行航迹规划，俞宬等[9]提出一种基于向量场直方图算法启发的改进B-RRT*无人机往返航迹规划算法。采用直角直方图网格对工作空间中的障碍进行统计表示，引入目标扇区和可通行扇区的概念，使用成本函数来引导无人机的运动，最后提出了一个航迹修剪操作，通过碰撞检测来剔除无效节点，并进一步修剪航路点，以得到一条更优的航迹路线。

3 智能仿生算法

智能仿生算法是一种模拟自然界生物行为和思维规律的优化算法，其运行原理主要基于神经网络规划、模糊逻辑规划以及基于仿生的行为模型。智能仿生算法可以在短时间内对复杂的连续问题和离散的非确定性多项式问题（Nondeterministic Polynomially， NP）组合优化找到可行的解决方案。智能仿生算法常具有以下共同特点：操作都是在每一代的个体上进行的；搜索是基于迭代进化的；多种群方案的并行执行是一种简便方法；这些方案通常能找到比较接近最佳的较优解；但由于迭代过程具有一定的随机性，无法保证每次得到完全相同的解。可以通过统一抽象问题变量，使用适应度函数来表示目标，随后利用每次迭代操作和进化来修改解空间中的种群。该算法主要基于种群迭代模式，通过操作每一代中的个体，获取解决方案空间中的有益信息，并逐步找到更优的位置。在无人机航迹规划中，智能仿生算法能够为无人机快速找到一组具备适应性和良好鲁棒性的可行解。

3.1 粒子群算法

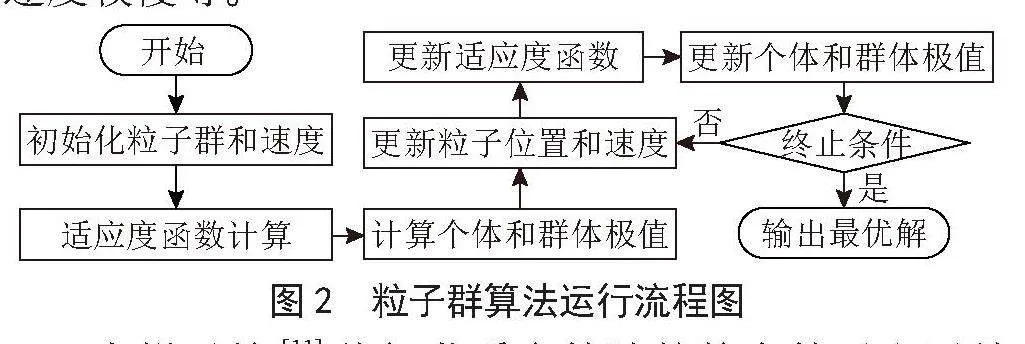
粒子群优化（Particle Swarm Optimization， PSO）是一种通过模拟鸟群觅食行为来进行全局优化的方法，由Kennedy等[10]于1995年首次提出。粒子群算法是一种用于解决连续空间优化问题的启发式算法，并且可以轻易地扩展到解决离散空间的优化问题。PSO算法的基本思想是：在搜索空间中随机生成一群粒子，每个粒子都有一个“个体最优解”（pBest）记录自己历史上的最佳位置，同时群体中的所有粒子共同分享一个“全局最优解”（gBest）记录整个群体历史上的最佳位置，在每一次迭代中，粒子会根据个体最优解和全局最优解来更新自己的速度和位置，如图2所示。PSO算法的优势在于它的简单性和易于实现，同时它也已经被成功应用于许多优化问题中。然而，PSO算法也有其局限性，例如可能会陷入局部最优解，或者在高维复杂的搜索空间中收敛速度较慢等。

李锐君等[11]将细菌觅食算法的趋向算子和迁徙算子结合至基础粒子群算法中，趋向算子有效提高了算法的局部搜索性能，解决了因粒子速度过快而错过最优解的问题。迁徙算子则扩大了寻优范围，并有助于避免算法陷入局部最优解。

吴钧皓等[12]提出了一个新的多无人机航迹规划问题（MUAVPP）的数学模型，设计了带交叉策略的粒子群算法（PSO-X）以解决此问题。将粒子群分为优势子群和普通子群，由此提高了粒子群对全局和局部的搜索能力。优势子群通过加入一种交叉策略进行更新，普通子群则使用样例学习策略进行更新并开发了一套编解码策略，使得算法能够有效地处理无人机航迹规划的决策变量，考虑到MUAVPP中存在续航约束，在适应度函数中加入惩罚系数，可以处理不可行解的同时引导算法向可行解收敛，确保算法能够更快找到可行解。

针对复杂和危险环境下的无人机航迹规划，智瀚宇等[13]提出了一种基于粒子群优化（PSO）算法和灰狼优化（GWO）算法的复合算法，称为PSO-GWO复合算法。该算法利用了非线性控制参数和加权自适应的个体位置更新策略来加快算法的收敛速度和提高算法解的最优性；采用随机指导策略来增加算法解的多样性，以此来提高算法的全局搜索能力，有助于避免陷入局部最优解。此外，使用了B样条曲线来平滑航迹，使得其更符合无人机的飞行姿态，进一步节省无人机的耗能。

3.2 蚁群算法

蚁群算法是一种模拟自然界蚁群觅食行为的计算机算法，由Dorigo[14]等人于20世纪90年代初提出。这种算法主要应用于求解组合优化问题。在搜寻食物时，蚂蚁会在其走过的道路上释放一种被称作信息素的标记物质，并依据这种物质的浓度来决定其移动的方向。蚂蚁倾向于向信息素浓度较高的地方移动，当大量蚂蚁一起寻找食物时，它们的行为就能产生一种正向的信息素反馈机制。蚂蚁觅食的运行轨迹模式如图3所示。

除以上通过蚂蚁利用信息素进行相互通信之外，常见的人工蚂蚁搜索还会建立禁忌表，即一只蚂蚁搜索过的航迹在下次搜索时就不再被该蚂蚁选择，并通过蚂蚁的集群活动使得算法更加智能化。通过这种方式，蚁群能够在一定程度上找到问题的最优解或者近似最优解。蚁群算法为解决处理复杂的组合优化问题提供了新的思路，并且由于蚁群算法的求解结果不依赖于初始路线的选择，而且在搜索过程中不需要进行人工调整，因此蚁群算法具有较强的鲁棒性。对于大规模问题，即使每只蚂蚁的探索过程相对独立，仅通过信息素交流，可以在问题空间的多个地点同时开始独立搜索，但是在大规模问题下算法的计算效率仍会无法满足实际需求，且常会陷入局部最优解。因此，在实际应用中通常需要引进新的改进策略来优化蚁群算法。

针对基本蚁群算法在解决TSP时遇到的停滞和早熟问题，赵鑫等[15]提出了一种带有遗忘因子的蚁群优化算法（FFACO）。通过在人工蚂蚁中加入遗忘因子，建立了一个新的状态转移公式，并修改了信息素更新策略。通过新的状态转移公式与当前解的误差率组合调整了对应的状态转移方程，以期降低最优值的误差和其追踪能力。修改后的航迹模型可以计算每条航迹到当前最优解的概率，此种算法优化不仅能缩短耗时，还能提供更好的航迹寻优结果。

于全友等[16]构建了一个带续航约束的无人机全覆盖航迹规划的数学模型，并提出了无人机返航时机判断机制和返航点计算方法，特别是设计了距离矩阵动态更新机制以处理返航点导致的节点拓扑结构的动态变化问题，并设计了滚动权值加权和信息素更新机制来兼顾全局启发性和局部启发性信息，提高了蚁群算法的搜索能力，基于改进蚁群算法优化了有续航约束条件的无人机全覆盖航迹规划。

孔维立等[17]引入避障策略并改进了人工势场法加入到启发函数中，使得蚂蚁在启发过程中不仅避开障碍物而且受到人工势场的引导，增强了搜索过程中的方向性。并通过设置信息素挥发因子的动态随机更新机制，算法在增加局部搜索能力的同时，避免了过早陷入局部最优。并结合了改进人工势能法进行预搜索的信息素初始化，增加预搜索后蚂蚁的局部搜索能力，加快了算法的收敛速度。

3.3 人工蜂群算法

人工蜂群算法（Artificial Bee Colony， ABC）由Karaboga[18]在2005年提出，主要用于解决实值函数优化问题。这个算法主要是模拟蜜蜂觅食过程中的信息交流和搜索行为。在蜜蜂群体中，蜜蜂可以被划分为三类：工蜂、观察蜂和侦查蜂。

工蜂负责搜索食物源，随后返回巢穴，通过舞蹈来传达搜索到的食物源；观察蜂在巢穴内部等候，观察工蜂的舞蹈以获取食物源信息，并根据这些信息决定去哪个食物源采集食物；当食物源被采集完或者长时间找不到新的食物源时，侦查蜂就会随机搜索新的食物源。

人工蜂群算法是以自然现象为原理得出的，具有良好的动态响应性。在ABC算法中，食物源对应于问题的解，而食物源的质量则对应于解的优越程度。工蜂和观察蜂通过搜索和学习食物源（解）来寻找最优解，侦查蜂则通过随机搜索来保持算法的多样性，避免算法过早陷入局部最优。ABC算法的主要步骤包括初始化、工蜂阶段、观察蜂阶段和侦查蜂阶段。在每个阶段，蜜蜂会根据预定的搜索策略更新当前的解，并通过贪心选择规则选择一个更优的解。

Akay等[19]检验了人工蜂群算法（ABC）在无约束大规模基准问题上的性能。研究发现ABC算法在大规模无约束优化问题上优于差分算法（DE）和粒子群优化算法（PSO）。这种优越的性能归功于ABC算法有效平衡探索和开发过程的能力，因为它使用了贪婪的选择、概率选择、随机选择这三种不同的选择算子。

Gao等[20]将多群体技术（Multipopulation Technique）与两种搜索机制结合到人工蜂群算法（ABC）中。多群体技术通过将整个种群P基于个体的空间位置划分为多个子群体，从而促进邻域的利用，而不会损失种群多样性。这种划分方式可以使算法将个体分配到不同的子区域，从而在每个子群体中通过ABC生成候选个体。并提出了两种搜索机制用作雇佣蜂和观察蜂的搜索方程，来促进每个子群体内部以及不同子群体之间的信息交流，并使得更优个体具有指导搜索方向的潜力。这种改进能使其更好地利用邻近个体信息，并通过新的搜索方程来获得更优解。

伍鹏飞等[21]围绕无人战斗机（UCAV）的航迹规划问题展开研究，构建了Zaslavskii混沌序列与蜂群算法相结合的方法，优化了蜜源的选择和搜索策略，加快了收敛速度，提高了算法的优化精度。

3.4 算法对比

在实际应用中，需要根据无人机的具体任务和实战环境选择合适的算法或将多种算法结合起来，不同的算法有着不同的特点，根据以上对全局航迹规划算法的探讨，对于这些算法的总结如表1所示。

4 局部规划算法

局部规划算法是指在已知环境中，通过分析当前所处位置的局部信息来进行航迹规划的方法。局部规划算法因其较高的适应性，常被用于解决动态环境变化下的避障问题。

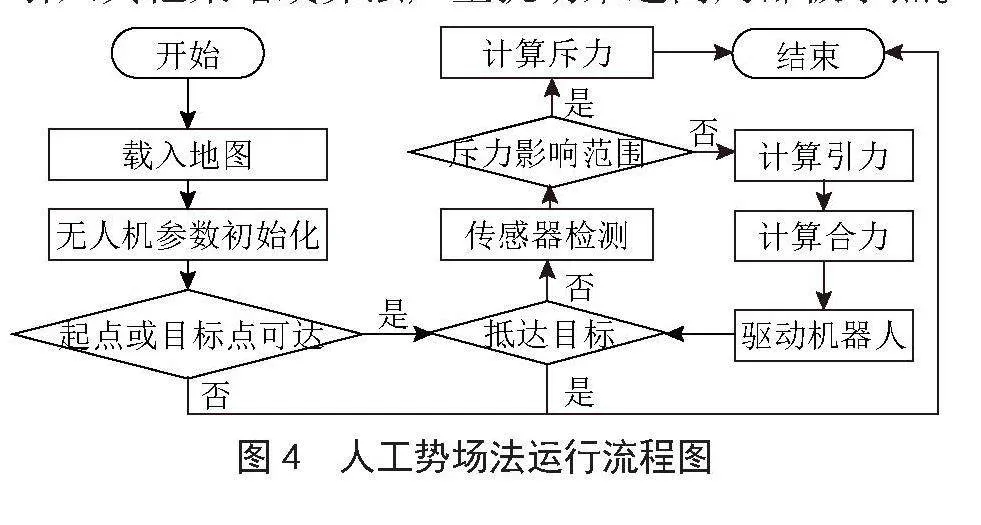
人工势场法是一种常见的局部规划算法，最早由Khatib[22]在1985提出。它通过构建一个虚拟的力场来引导无人机沿着期望的航迹移动。当无人机接近障碍物时，斥力对其作用使之改变方向，反之，引力的作用会使其向目标点靠近。通过调整斥力和引力的大小和方向，可以使无人机在复杂环境中实现稳定、平滑的航迹规划，如图4所示。人工势场法所具备的实时性好以及计算简便等特点，使其在简单障碍物环境下的实时航迹规划中具有良好的适应性。但易陷入局部极小值，难以处理复杂环境中的航迹规划，可以选择引入其他策略或算法产生扰动来逃离局部极小点。

动态窗口法是另一种适用于无人机航迹规划的局部规划算法，最早由Fox[23]在1997年提出。它通过将无人机的运动范围划分为多个小区域，并为每个区域分配一个权重值，以表示该区域对无人机运动的影响程度。在规划过程中，无人机会根据当前位置和目标位置选择具有最大权重的区域作为下一个运动目标。动态窗口法具有较强的适应性和实时性，能够在不断变化的环境中为无人机提供合适的移动策略，但搜索空间受到速度空间采样的限制，可能无法找到最优解，可以通过调整窗口大小、采样密度或结合其他航迹规划算法来改善性能。

当目标引力与障碍物斥力大小相等且方向相反时，无人机由于对周围环境的感知存在局限性，容易在传统的人工势场法作用下陷入局部极小点，卢艳军等[24]提出了“选择穿越法”以解决此种情况。当无人机飞到一个局部极小点且无法继续前进时，则激活选择穿越行为。局部极小点的特点是无人机悬停，且两边紧邻障碍物。此时判断无人机在航迹规划上的下一个位置是否能更接近目标点，如果不能，就激活选择穿越行为。使用传感器来获取两个障碍物之间的距离，判断它们之间的距离是否满足安全的穿越条件，如果满足，则提高引力函数中的引力系数。通过加大目标点对无人机的吸引力，使无人机能够跳出局部极小点并继续向目标前进。如果不满足，则调整合斥力的作用方向，将其沿逆时针增加π/2 rad，以此来使无人机改变运动方向，逃离局部极小点。

涂柯等[25]在无人机陷入局部极小时引入调控力，帮助无人机逃离陷阱。此外，由于障碍物的影响可能导致无人机躲避障碍物时偏离原有航迹，使得航迹过长。故作者引入了一个检测因子，该因子确保在障碍物产生斥力为有效斥力时，无人机能够检测并避开障碍物，而当斥力被视为无效时，则无人机将不会改变其航迹以躲避障碍物，该改进方法可以在不牺牲安全性的情况下减小航迹长度，从而优化避障航迹。

Wu等[26]提出了旋转人工势场法（R-APF）。它针对传统的APF算法进行了改良，使其适应三维空间的应用，R-APF增加了目标点对无人机的吸引力，并赋予了无人机一种逃逸力，使得无人机在遇到局部最小点时能够“逃离”，并将应用范围拓宽到了三维空间。还结合了优化的VINS-Mono障碍物检测算法来感知周围环境，并创建环境中障碍物的栅格化地图，进一步利用R-APF进行航迹规划以实现避障。R-APF有效提高了无人机避障航迹规划的稳定性和成功率，在无人机障碍物避让和大范围区域操作方面表现优越，这些改进使得算法在实际应用场景的可靠性和适用性方面得到了提升。

5 存在的问题与建议

不同的航迹规划算法有着不同的特点，国内外学者对于算法改进也做出了大量的研究，但仍存在几方面的难题亟待解决，如未知环境下无人机环境感知问题，多无人机航迹协同问题等，具体如下：

1）在航迹规划算法中，常将飞行距离和飞行时间作为规划的重点条件，诸如燃料损耗、飞行转角等因素往往没有被充分考虑，如在固定翼无人机航迹规划中需考虑dubins转角；多旋翼无人机若转角航迹不够平滑，速度损耗过大，将会导致飞行时间过长等问题。

2）对于无人机在未知环境内进行航迹规划，无人机必须利用传感器实时探测环境数据，传统的算法可能无法处理庞大的计算量，导致航迹生成效率偏低。

3）多无人机航迹协同存在着信息共享方面的问题，并且需权衡单架无人机的航迹优化和整个无人机群的任务分配，需做到航迹最短、能耗最小、任务完成时间最短等要求，单个简单的算法面对这种问题往往显得捉襟见肘，需融合多个算法进行处理。

针对上述问题与无人机航迹规划算法的发展，建议如下：

1）可通过在航迹规划算法中引入额外代价来优化大转角，或者以使转角变化最小化为目标进行算法设计，这样可以在平滑航迹的同时，减少因转向而产生的额外损耗；还可以通过将无人机的飞行动力学模型整合到航迹规划中，辅助生成符合飞行性能限制的航迹以确保其可飞性，还可使用如贝塞尔曲线、B样条或者样条插值等样条曲线来平滑航迹。

2）未知环境下的无人机航迹规划可在RRT算法基础上进行改进，如融合A*算法将航迹规划分为高层和底层决策，其中高层负责生成大致方向和目标点，低层负责处理具体的避障和航迹细节，以实现快速寻找合理航迹并在环境变化下实时更新的目的；还可使用训练好的神经网络来快速预估最佳航迹或行动方案，以期减少实时规划的计算量。

3）处理多无人机航迹协同问题的关键是将多种算法和优化策略有效融合，并确保各个算法在特定情境下能使效果最优化，具体可以使用粒子群算法等智能仿生算法来优化整个无人机群的航迹配置，并采用动态窗口法、人工势场法等进行无人机的实时避障来保证飞行安全，使无人机群体适应性策略能够应对环境变化和每架无人机的实时动态变化。

6 结 论

本文在无人机航迹规划算法方面进行了详细概括，并给出了相应的结论与评价。全局规划算法在动态环境中存在变化不够灵活的弊端，但优势在于可结合全局特点规划出最优航迹；相反地，局部航迹规划算法虽动态适应性较强，但在全局状态下无法保障解的最优性。尽管当前的航迹规划算法已经取得了巨大进展，但在如何更好地应对无人机在不断变化的任务需求下的实际运作状况方面仍有很大的发展空间。因此，算法的实时执行性能、对环境变化的响应速度以及对计算资源的有效利用能力将成为未来航迹规划算法的重要评价指标。同时，目前在已知环境下存在简单障碍物的静态航迹规划算法已经非常成熟，未来的研究应着力于算法的融合与优化，结合全局规划的优势和局部规划的灵活性，针对多无人机问题以及动态变化的复杂环境提出更加高效和准确的混合型航迹规划算法，为实现更加智能、高效的无人机自主飞行打开新的篇章。

参考文献：

[1] 金泉，高显忠，郭正，等.无人机集群在机场封控作战中的应用研究 [J].飞航导弹，2021（10）：52-58.

[2] 王辰.多旋翼无人机在军事后勤领域中的应用及发展趋势分析 [J].飞航导弹，2021（8）：56-60.

[3] HART P E，NILSSON N J，RAPHAEL B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths [J].IEEE Transactions on Systems Science and Cybernetics，1968，4（2）：100-107.

[4] CHEN J C，LI M Y，YUAN Z Y，et al. An Improved A* Algorithm for UAV Path Planning Problems [C]//2020 IEEE 4th Information Technology，Networking，Electronic and Automation Control Conference （ITNEC）.Chongqing：IEEE，2020，1：958-962.

[5] 唐嘉宁，彭志祥，李孟霜，等.基于改进A*算法的无人机路径规划研究 [J].电子测量技术，2023，46（8）：99-104.

[6] ZHANG Z，WU J，DAI J Y，et al. Optimal Path Planning with Modified A-Star Algorithm for Stealth Unmanned Aerial Vehicles in 3D Network Radar Environment [J].Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering，2022，236（1）：72-81.

[7] LAVALLE S M. Rapidly-exploring Random Trees： A New Tool for Path Planning [R].Ames：Iowa State University，1998.

[8] 顾子侣，刘宇，孙文邦，等.基于RRT的无人机动态航路规划算法 [J].计算机科学，2023，50（S1）：65-69.

[9] 俞宬，陈谋，雍可南.基于改进RRT*算法的无人机往返航迹规划 [J].中国科学：技术科学，2023，53（11）：1911-1921.

[10] KENNEDY J，EBERHART R. Particle Swarm Optimization [C]//Proceedings of ICNN'95 International Conference on Neural Networks.Perth：IEEE，1995：1942-1948.

[11] 李锐君，董素鸽.基于粒子群算法的无人机灭火路径规划仿真 [J].计算机仿真，2023，40（9）：43-48.

[12] 吴钧皓，戚远航，罗浩宇，等.带交叉策略的粒子群算法求解多无人机路径规划问题 [J].工业控制计算机，2023，36（10）：94-95+168.

[13] 智瀚宇，贾新春，张学立.无人机路径规划：一种粒子群和灰狼复合算法 [J/OL].控制工程，2023：1-8（2023-11-28）.https：//doi.org/10.14107/j.cnki.kzgc.20221058.

[14] DORIGO M，MANIEZZO V，COLORNI A. Ant System： Optimization by A Colony of Cooperating Agents [J].IEEE Transactions on Systems， Man and Cybernetics， Part B （Cybernetics），1996，26（1）：29-41.

[15] 赵鑫，杨雄飞，钱育蓉.改进的蚁群优化算法求解旅行商问题 [J].计算机工程与设计，2022，43（4）：962-968.

[16] 于全友，徐止政，段纳，等.基于改进ACO的带续航约束无人机全覆盖作业路径规划 [J].航空学报，2023，44（12）：303-315.

[17] 孔维立，王峰，周平华，等.改进蚁群算法的无人机三维路径规划 [J].电光与控制，2023，30（3）：63-69.

[18] KARABOGA D. An Idea Based on Honey Bee Swarm for Numerical Optimization [R].Technical Report TR06.Kayseri：Erciyes University，2005.

[19] AKAY B，KARABOGA D. Artificial Bee Colony Algorithm for Large-scale Problems and Engineering Design Optimization [J].Journal of Intelligent Manufacturing，2012，23（4）：1001-1014.

[20] GAO W F，HUANG L L，LIU S Y，et al. Artificial Bee Colony Algorithm Based on Information Learning [J].IEEE Transactions on Cybernetics，2015，45（12）：2827-2839.

[21] 伍鹏飞，李涛，曹广旭，等.基于改进混沌蜂群算法的无人战斗机路径规划 [J].中国科技论文，2021，16（3）：301-306.

[22] KHATIB O. Real-time Obstacle Avoidance for Manipulators and Mobile Robots [C]//1985 IEEE International Conference on Robotics and Automation.Saint Louis：IEEE，1985：500-505.

[23] FOX D，BURGARD W，THRUN S. The Dynamic Window Approach to Collision Avoidance [J].IEEE Robotics & Automation Magazine，1997，4（1）：23-33.

[24] 卢艳军，李月茹.基于改进人工势场法的四旋翼飞行器航迹规划 [J].火力与指挥控制，2018，43（11）：119-122+127.

[25] 涂柯，侯宏录，苏炜.改进人工势场法的无人机避障路径规划 [J].西安工业大学学报，2022，42（2）：170-177.

[26] WU Z Y ，DONG S P，YUAN M，et al. Rotate Artificial Potential Field Algorithm Toward 3D Real-time path Planning for Unmanned Aerial Vehicle [J].Proceedings of the Institution of Mechanical Engineers， Part G： Journal of Aerospace Engineering，2023，237（4）：940-955.

DOI：10.19850/j.cnki.2096-4706.2024.17.010

作者简介：张琪（2001—），男，汉族，天津人，硕士在读，研究方向：无人机航迹规划；通信作者：张志学（1982—），男，汉族，河北沧州人，讲师，博士，研究方向：无人机警务应用。

收稿日期：2024-03-13

基金项目：公安部理论与软科学项目（2022LL56）；河北省省级科技计划（20375601D）；警察大学学生科技创新计划项目（yjskc22035）

Research Progress on UAV Trajectory Planning Algorithm

ZHANG Qi1， REN Yuchen1， GU Tengda1， JI Jinqi2， ZHANG Zhixue3

（1.Graduate School， China People's Police University， Langfang 065000， China;

2.School of Chemistry and Chemical Engineering， Tianjin University of Technology， Tianjin 300384， China;

3.School of Policing Command， China People's Police University， Guangzhou 510663， China）

Abstract： At present， the development of UAV technology has made obvious breakthroughs， and the application fields of UAV have expanded from military to commerce， scientific research， entertainment and other fields. This paper takes the UAV trajectory planning algorithm as the research object. Firstly， according to the principle and characteristics of the trajectory planning algorithm， this paper divides it into two categories of global planning algorithm and local planning algorithm， among which the global planning algorithm can be divided into the graph search6exMr82U53J61mdrAS4ZRw== algorithm and intelligent bionic algorithm. Secondly， the principles， workflow， advantages and disadvantages of the algorithms are analyzed in depth， the corresponding improvement methods are introduced， and their applications in the corresponding fields are elaborated in combination with the characteristics of the algorithms. Finally， it discusses the limitations and challenges of the above algorithms in the practical application， looks forward to the development trend of the future trajectory planning technology， and points out the direction for the research of UAV trajectory planning algorithm.

Keywords： UAV; trajectory planning; global planning algorithm; local planning algorithm; graph search algorithm; intelligent bionic algorithm