基于改进幂次趋近律的机械臂终端滑模轨迹跟踪控制

摘 要：针对传统终端滑模在机械臂轨迹跟踪控制中存在抖振、收敛速度缓慢及奇异性问题，提出了一种基于改进幂次趋近律的有限时间非奇异终端滑模控制策略。首先，设计了一种既能快速收敛又能消除系统初始抖振的改进幂次趋近律，分析证明了其有限时间收敛特性。然后，提出了一种快速非奇异终端滑模面，使系统误差能在有限时间内收敛到零，在此基础上，设计了基于改进幂次趋近律的机械臂快速非奇异终端滑模轨迹跟踪控制器，并进行Lyapunov稳定性分析。仿真结果表明：该控制器能准确跟踪期望轨迹，跟踪误差能在有限时间内快速收敛到平衡点，有效削弱了系统抖振，与快速幂次趋近律的普通非奇异终端滑模控制相比，具有更快的收敛速度和更好的控制效果。

关键词：机械臂；终端滑模；改进幂次趋近律；轨迹跟踪；抖振

中图分类号：TP242 文献标识码：A 文章编号：2096-4706（2024）17-0173-06

0 引 言

机器人实现某种作业实际上是使机器人跟踪期望轨迹的控制问题。因此，研究具有较高跟踪精度的控制策略，一直都是机器人控制研究领域中的重点与热点问题，典型的控制算法有PID控制[1]、自适应控制[2-3]、滑模变结构控制[4-6]及神经网络控制[7-8]等，以上各种控制策略各有所长，也存在不足。其中，由于滑模控制可以使系统按照设计的滑动模态运动，与系统参数摄动和外界干扰完全无关，具有很强的鲁棒性，可以削弱负载变化或干扰对系统性能产生的影响，特别适合机器人控制。

普通线性滑模在到达滑动模态后，跟踪误差不能在有限时间内收敛至零。1988年，Zak提出终端吸引子概念，产生了终端滑模控制策略。终端滑模在滑动超平面的设计中引入非线性函数，使跟踪误差能在有限时间内收敛到平衡点。如文献[9]提出了一种机械手有限时间收敛的全局非奇异终端滑模控制器，通过设计非奇异终端滑模面，消除传统终端滑模控制的奇异性问题。文献[10]针对不确定机器人设计了一种全局有限时间终端滑模控制方法，为了消除奇异性，提出了一种新型积分滑模面，证明了系统的有限时间收敛特性。文献[11]提出了一种新型包含反正切函数的非奇异终端滑模面，设计了具有鲁棒性的快速非奇异终端滑模控制律，以确保系统状态在有限时间内全局收敛到原点。终端滑模和线性滑模均存在抖振问题，控制的不连续性是抖振产生的根本原因。为使滑模变结构控制在各领域更好地发展和应用，很多专家学者提出了各种方法来抑制抖振，主要有边界层法[12-13]、趋近律法[14-15]、高阶滑模控制[16]等。

本文在以上文献分析的基础上，提出了一种基于改进幂次趋近律的机械臂快速非奇异终端滑模轨迹跟踪控制策略，在降低系统抖振的同时保证具有较快的收敛速度和较高的控制精度，从而实现机械臂的精确位置跟踪。

1 改进幂次趋近律及其特性分析

1.1 改进幂次趋近律设计

滑模控制的到达条件虽然能确保系统状态到达滑模面，但不能反映它是如何趋近滑模面的，因此，可利用趋近律来保证正常运动阶段的品质。高为炳提出了三种常用趋近律：等速趋近律、指数趋近律和幂次趋近律。其中，等速趋近律速度恒定不能灵活调整；指数趋近律趋近速度快，但在接近滑动模态时抖振较大；幂次趋近律虽然能削弱系统初始抖振，但趋近速度过小。因此，为改善传统趋近律的不足，研究人员提出了一些改进趋近律，如快速幂次趋近律、双幂次趋近律、多幂次趋近律等。

本文在分析常用趋近律基础上，提出了一种改进的幂次趋近律：

（1）

式中，k1，k2，k3＞0，a＞0，0＜ρ＜1，e-at为指数函数。

当系统状态远离滑模面（|s|＞1）时，-k1s-k3|s|3sgn（s）项起主要作用。而当系统接近滑模面（|s|＜1）时，-k1s-k2|s|ρe-atsgn（s）项起主导作用，衰减因子eat的作用是在系统趋近滑模面（s=0）的过程中减小-k2|s|ρsgn（s）项的趋近速度，实现滑模面的平滑过渡。式（1）中的后两项，相当于对系统采用了分段控制，利用-k1s项来平滑分段的不连续性。此外，由式（1）知，当s→0+或s→0-时，ṡ=0，表明改进幂次趋近律在趋近滑模面时不会产生抖振现象。

1.2 改进幂次趋近律有限时间收敛特性分析

定理1 对于系统（1），s和ṡ将在有限时间Tr内收敛到平衡点，即当t＞Tr时，，其中：

（2）

式中，s0为s的初始值。

证明：根据滑模到达条件，由（1）式得：

因此，改进幂次趋近律满足滑模到达条件。

假设s0＞1，分两个阶段计算有限时间Tr：

1）系统从s0到达s=1，所用时间为t1。

当s0＞1时，趋近律中-k1s-k3|s|3sgn（s）起主要作用，即：

（3）

对其变形，可得：

（4）

令y=s-2，则，式（4）变为：

（5）

式（5）的通解为：

（6）

式（6）可化简为：

（7）

根据条件：

（8）

解得：

（9）

2）系统从s=1到达s=0，所用时间为t2。

当0＜s＜1时，趋近律-k1s-k2|s|ρe-atsgn（s）起主导作用，即：

（10）

具体推导过程同第一阶段，可求得：

（11）

同理，当s0＜-1时，计算过程与计算结果同s0＞1。

综上所述，由于计算系统收敛时间时忽略了次要因素的影响；因此，系统总的收敛时间：

（12）

至此，定理1得以证明。

由式（9）、式（12）可知，收敛时间Tr受系统初始状态s0的影响，s0越大，收敛时间越长。

2 非奇异终端滑模轨迹跟踪控制器设计

2.1 机械臂动力学模型

n关节机械臂的动力学模型为：

（13）

式中，q，，分别为机械臂各关节的位置，速度和加速度向量；M（q）为对称惯性矩阵；为离心力和哥氏力矢量；G（q）为重力向量；τ为广义力矩向量；f为建模误差和外部扰动，假设f有界，即：

，λ0，λ1，λ2＞0。

2.2 快速非奇异终端滑模面设计

引入关节位置误差：

e=q-qd （14）

式中，e=（e1，…，en）T，q为各关节实际角度，qd为各关节的期望关节角度。

普通非奇异终端滑模面（NTSM）为：

（15）

式中，s=（s1，…，sn）T，β=diag（β1，…，βn），βi＞0，p，q为正奇数，且1＜p/q＜2。

由式（15）可知：当 时， ，导致滑模面不稳定；因此，设计快速非奇异终端滑模面（FNTSM）为：

（16）

式中，α=diag（α1，…，αn），αi＞1，其他参数的定义同式（15）。

定理2：当系统到达式（16）表示的滑模面后，对于任意ei（Tr）≠0，系统稳定并将在有限时间Ts内收敛到零，且收敛时间小于式（15）表示的滑模面。

证明：取Lyapunov函数

对上式求导，在系统到达滑模面后，si=0，结合式（16）可得：

当且仅当时，。

设系统到达滑模面后，从ei（Tr）≠0到ei（T）=0所用时间为Ts。当时，由式（16）得：

（17）

对式（17）两边积分，可得：

（18）

当时，可得到相同的结果。

同理，当，求得式（15）滑模面的收敛时间为：

（19）

对比式（18）和式（19），由于0＜αi-q/p＜1，故Ts<Ts′，即快速非奇终端滑模面式（16）的收敛时间小于式（15）表示的滑模面。

2.3 轨迹跟踪控制器设计

基于改进幂次趋近律的机械臂终端滑模轨迹跟踪控制器结构框图如图1所示。

控制器包括两部分：由系统状态参数和终端滑模面所决定的等效控制项τeq和根据改进幂次趋近律得到的切换控制项τsw，即：τ=τeq+τsw。

当系统到达滑模面时，即：，求得等效控制τeq，对式（16）取导，联合式（13），可得：

（20）

结合式（1），令系统的改进幂次趋近律为：

（21）

式中，sig（s）ρ=[|s|ρ，…，|sn|ρsgn（sn）]T，K1=diag（k11，…，k1n），K2=diag（k21，…，k2n），K3=diag（k31，…，k3n），k1i＞0，k2i＞0，k3i＞0，sig（s）3定义同sig（s）ρ。

切换控制τsw可设计为：

（22）

由此求得基于改进幂次趋近律的机械臂快速非奇异终端滑模轨迹跟踪控制律：

（23）

定理3 对于n关节机械臂（13），选取式（23）表示的控制律，则机械臂闭环控制系统稳定。

证明：取Lyapunov函数。则：

将式（22）代入上式，得：

令：，γi≥0，则上式可变为：

满足李雅普诺夫稳定性定理。

3 仿真实验分析

以二关节机械臂作为仿真实验对象，动力学模型采用式（13）。其中：

式中，r1=1 m，r2=0.8 m，J1=J2=5 kgm，m1=0.5 kg，m2=1.5 kg。

机械臂关节空间期望轨迹取摆线运动方程：

，

。

设系统初始状态为：q1（0）=0.5，q2（0）=-0.5， ，。系统建模误差和外部扰动参数取为：λ0=0.1，λ1=0.2，λ2=0.3，滑模控制参数取：a=0.2，ρ=1/3，p/q=5/3，，，。

采用Simulink搭建仿真模型，利用S函数描述被控对象和控制器。为验证本文提出的轨迹跟踪控制器性能的优越性，将其与基于快速幂次趋近律的普通非奇异终端滑模控制器进行比较。快速幂次趋近律表达式为：

基于快速幂次趋近律的普通非奇异终端滑模轨迹跟踪控制律可设计为：

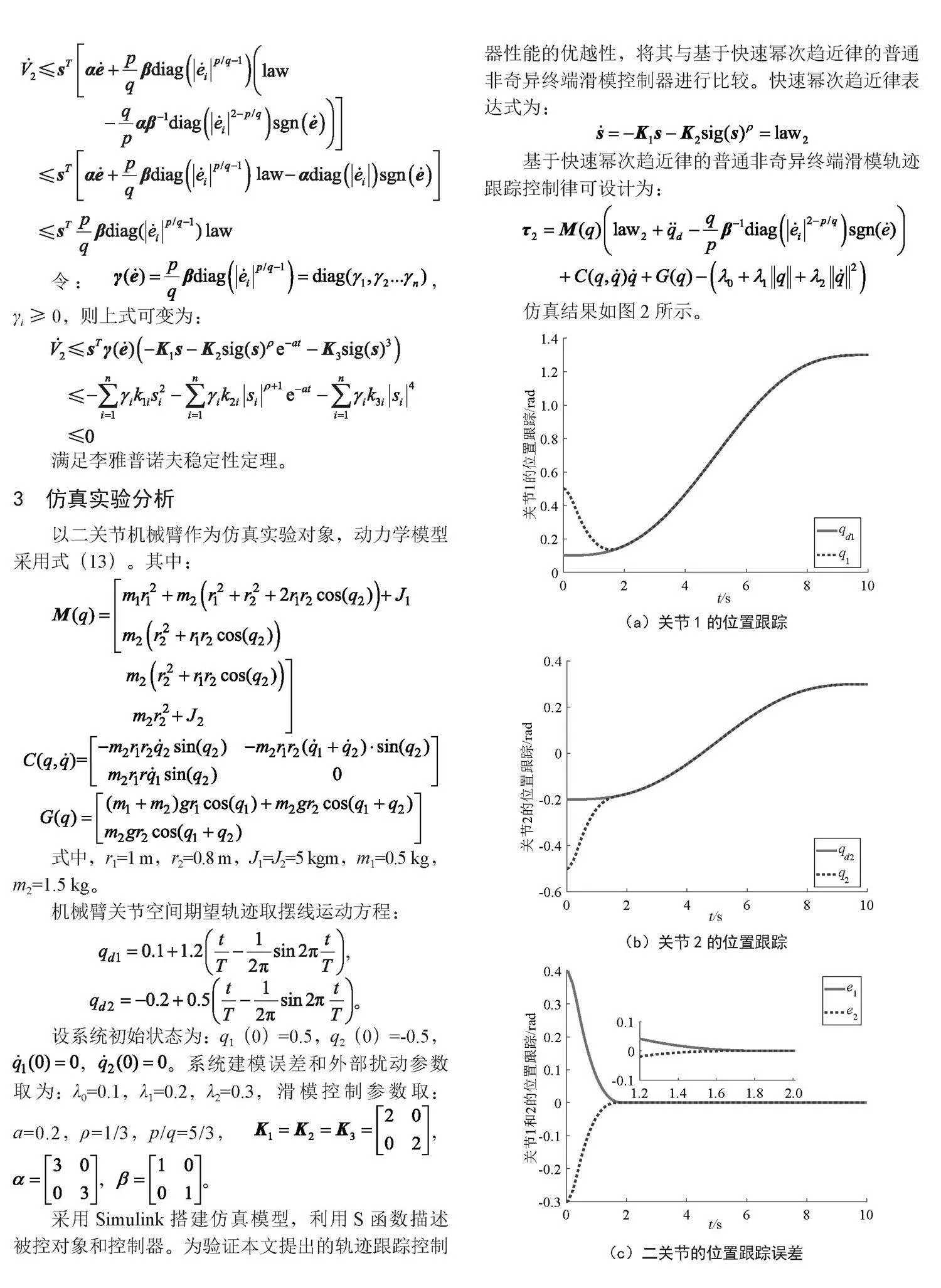
仿真结果如图2所示。

（a）关节1的位置跟踪

（b）关节2的位置跟踪

（c）二关节的位置跟踪误差

（d）控制输入

由图2可知：关节1和关节2能快速跟踪期望轨迹，跟踪误差的收敛时间分别为1.76 s和1.56 s。由于控制器中存在开关函数sign，使得关节1和关节2的控制输入有抖动，因此，为削弱系统抖动，将式（16）、式（21）、式（23）中的开关函数替换成饱和函数，也称边界层法，即在边界层外采用正常的滑模控制，在边界层内为连续控制。饱和函数表示为：

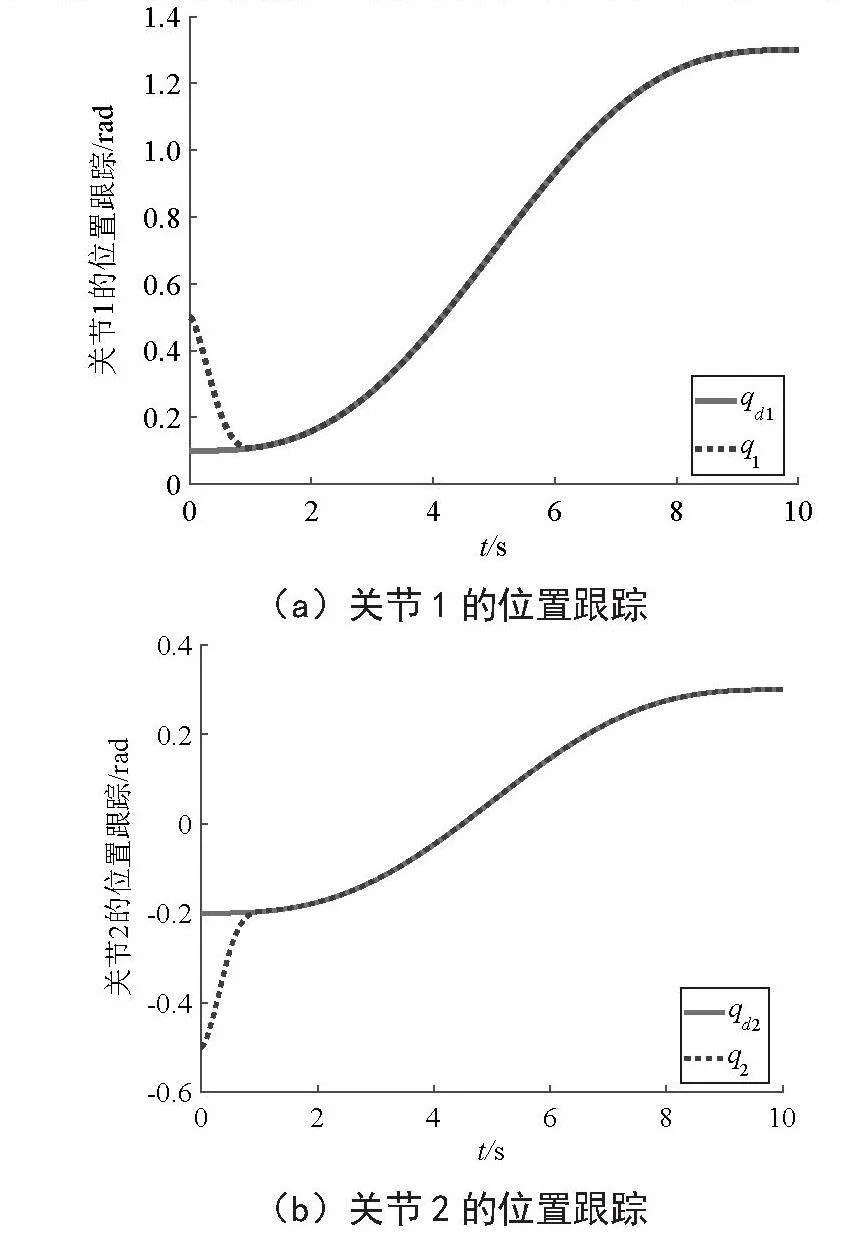
式中，δ为边界层厚度，δ越小，控制精度越高，但会使控制增益变大，抖振增强；反之，δ越大，抖振越小，但会使控制精度变差，为平衡系统控制精度和抖振，取δ=0.02。基于改进幂次趋近律的机械臂快速非奇异终端滑模控制的仿真结果如图3所示。

（a）关节1的位置跟踪

（b）关节2的位置跟踪

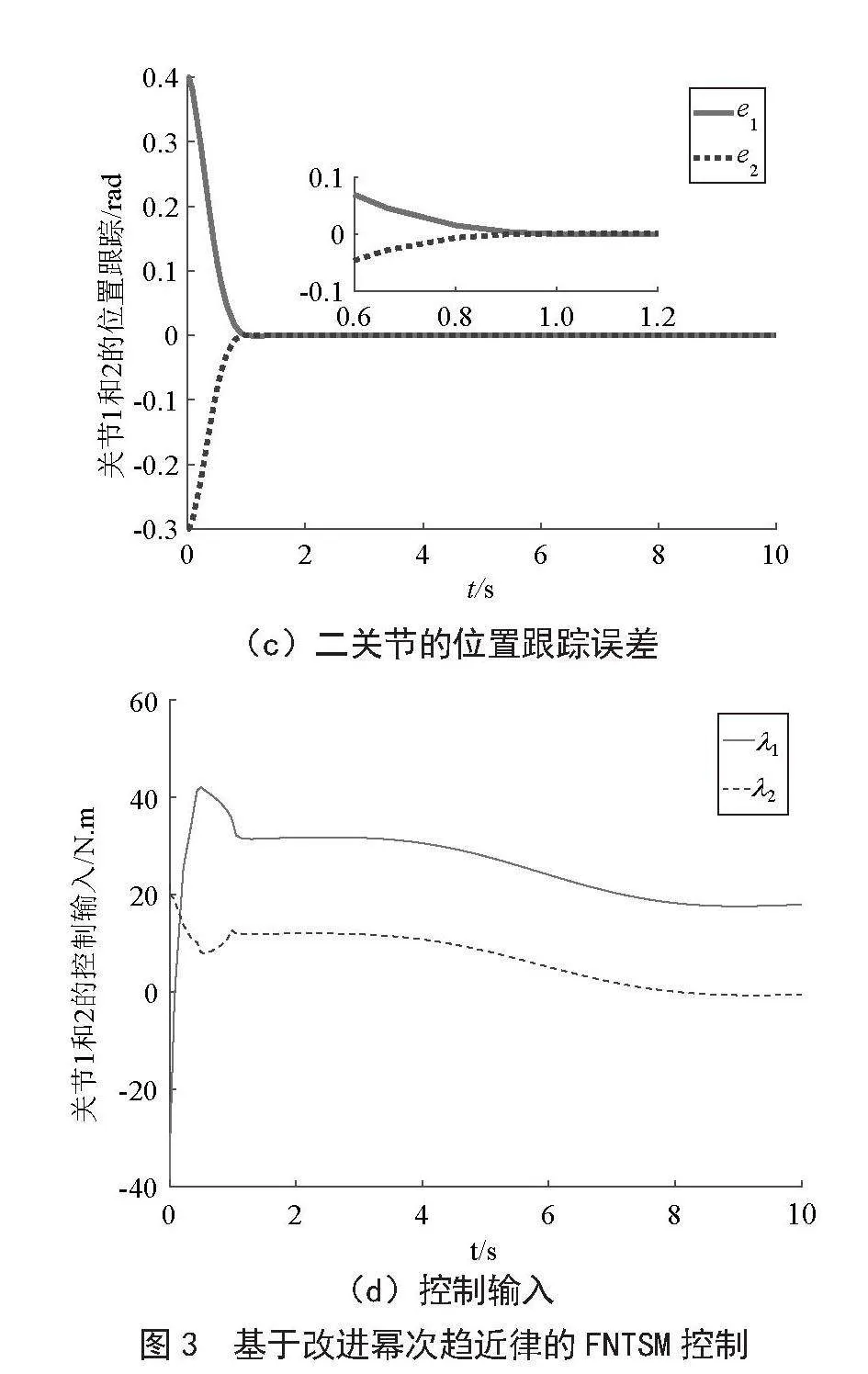
（c）二关节的位置跟踪误差

（d）控制输入

由图3可知：关节1和关节2的误差收敛时间分别为0.95 s和0.90 s，相比快速幂次趋近律的普通终端滑模轨迹跟踪控制器，收敛时间缩短了0.81 s和0.66 s，并且收敛时间与系统初始状态误差有关，初始误差越大，收敛时间越长。同时，对比图2（d）可知，引入饱和函数能有效削弱关节1和关节2的控制输入抖动，使控制输入平滑，表明本文提出的轨迹跟踪控制策略比基于快速幂次趋近律的NTSM控制具有更好的跟踪效果。

4 结 论

为提高系统趋近过程的动态品质，设计了一种有限时间收敛的改进幂次趋近律，在保证快速趋近的同时，不会产生抖振现象。提出的快速非奇异终端滑模面解决了普通终端滑模面的奇异性问题和收敛速度缓慢问题，并使系统跟踪误差能在有限时间内收敛到零。仿真结果表明，本文提出的基于改进幂次趋近律的机械臂快速非奇异终端滑模轨迹跟踪控制器能实现对期望轨迹的快速准确跟踪，并能有效抑制系统抖振现象的产生。在下一步的研究中，针对外部干扰和动力学模型的不确定性，可以利用干扰观测器或神经网络算法，实现对集总干扰的有效估计和控制器的在线补偿，进一步提高系统控制性能。

参考文献：

[1] 黄鹤，李文龙，杨澜，等.ICPA-LQR优化的两轮平衡机器人自稳定与轨迹跟踪PID控制器设计 [J/OL].哈尔滨工业大学学报，2025（5）：1-12（2022-11-09）.http：//kns.cnki.net/kcms/detail/23.1235.T.20221108.1333.002.html.

[2] TAHERI-KALANI J，ZAREI N. An Adaptive Technique for Trajectory Tracking Control of a Wheeled Mobile Robots Without Velocity Measurements [J].Automatic Control and Computer Sciences，2016，50（6）：441-452.

[3] 马淑华，王锦华，马贤春，等.移动机器人自适应轨迹跟踪控制 [J].火力与指挥控制，2022，47（8）：13-17+24.

[4] 陈正升，王雪松，程玉虎.考虑扰动与输入饱和的机械臂连续非奇异快速终端滑模控制 [J].控制与决策，2022，37（4）：903-912.

[5] SACHAN S，SWARNKAR P. Intelligent Fractional Order Sliding Mode Based Control for Surgical Robot Manipulator [J].Electronics （Basel），2023，12（3）：729.

[6] 王雪闯，王会明，赵振华.基于改进型积分终端滑模控制方法的移动机器人轨迹跟踪设计与实验 [J].控制与决策，2023，38（10）：2881-2887.

[7] 叶长龙，张思阳，于苏洋，等.基于神经网络的全方位移动机器人运动稳定性研究 [J].机器人，2019，41（4）：443-451.

[8] SHAO N F，ZHOU Q Y，SHAO C Y，et al. Adaptive Control of Robot Series Elastic Drive Joint Based on Optimized Radial Basis Function Neural Network [J].International Journal of Social Robotics，2021，13（7）：1-10.

[9] FENG Y，YU X H，MAN Z H. Non-singular Terminal Sliding Mode Control of Rigid Manipulators [J].Automatica，2002，38（12）：2159-2167.

[10] SU Y X，ZHENG C H. A New Nonsingular Integral Terminal Sliding Mode Control for Robot Manipulators [J].International Journal of Systems Science，2020，51（8）：1418-1428.

[11] ZHAI J Y，XU G. A Novel Non-Singular Terminal Sliding Mode Trajectory Tracking Control for Robotic Manipulators [J].IEEE Transactions on Circuits and Systems II： Express Briefs，2021，68（1）：391-395.

[12] 张贝贝，赵东亚，高守礼，等.自适应边界层非奇异快速终端滑模控制 [J].控制工程，2019，26（4）：717-723.

[13] MAKRINI I E ，RODRIGUEZ-GUERRERO C ，LEFEBER D，et al. The Variable Boundary Layer Sliding Mode Control： A Safe and Performant Control for Compliant Joint Manipulators [J].IEEE Robotics and Automation Letters，2017，2（1）：187-192

[14] TANG Q R，LI Y H，GUO R Q，et al. Chattering-suppression Sliding Mode Control of an Autonomous Underwater Vehicle Based on Nonlinear Disturbance Observer and Power Function Reaching Law [J].Transactions of the Institute of Measurement and Control，2021，43（9）：2081-2093.

[15] JI P，LI C L，MA F Y. Sliding Mode Control of Manipulator Based on Improved Reaching Law and Sliding Surface [J].Mathematics，2022，10（11）：1935.

[16] 易善超.基于高阶滑模的机械臂轨迹跟踪控制 [D].南京：东南大学，2019.

作者简介：王燕（1981—），女，汉族，河南驻马店人，副教授，博士，研究方向：机器人运动控制技术。

DOI：10.19850/j.cnki.2096-4706.2024.17.034

收稿日期：2024-03-02

基金项目：河南省科技厅科技攻关项目（242102311244）；河南省高等学校重点科研项目计划（23B413002）；河南省高等学校青年骨干教师培养计划（2019GGJS245）

Trajectory Tracking Control of Manipulator Terminal Sliding Mode Based on Improved Power Reaching Law

WANG Yan

（School of Electrical Engineering and Automation， Luoyang Institute of Science and Technology， Luoyang 471023， China）

Abstract： To solve the problems of chattering， slow convergence speed and singularity of the traditional terminal sliding mode in control for manipulator trajectory tracking， a finite-time non-singular terminal sliding mode control strategy based on improved power reaching law is proposed. Firstly， an improved power reaching law is developed， which can converge quickly and eliminate initial system chattering， and its finite-time convergence characteristic is analyzed and verified. Secondly， a fast non-singular terminal sliding mode surface is proposed， which enables the system error to converge to zero in a finite time. On this basis， the fast non-singular terminal sliding mode controller for manipulator trajectory tracking is designed based on improved power reaching law， and it is performed the Lyapunov stability analysis. Simulation results show that the controller can track the expected trajectory precisely and enable the tracking error to converge to the equilibrium point in finite time， which reduces the system chattering effectively. Compared with the ordinary non-singular terminal sliding mode controller with fast power reaching law， it possesses a faster convergence speed and better control effect.

Keywords： manipulator; terminal sliding mode; improved power reaching law; trajectory tracking; chattering