CHAID-RF：基于CHAID决策树的集成学习方法

摘 要：针对卡方自动交互诊断（CHAID）决策树易过拟合的问题，提出CHAID随机森林方法（CHAID Random Forest， CHAID-RF）。该方法采用随机采样、随机选择特征以及集成的策略，将CHAID决策树作为基分类器，形成CHAID-RF。为了验证CHAID-RF的有效性，选取CART、CHAID、SVM、RF作为对比算法，以准确率、加权查准率、加权查全率、加权F值作为分类模型评价指标，以均方根误差作为回归模型评价指标，采用10个分类数据集和7个回归数据集进行验证。实验结果表明CHAID-RF可行有效。

关键词：CHAID；随机森林；CHAID-RF；分类；回归

中图分类号：TP399 文献标志码：A 文章编号：2096-4706（2024）17-0028-09

0 引 言

决策树算法最早于1966年被提出，常用于分类和回归分析。经典的决策树算法有ID3、C4.5、CART、CHAID、Quest，之后的决策树主要关注最佳结点的选择问题进行决策树构造、改进和优化[1-4]。现有决策树算法的最佳结点函数选择，主要偏向于信息熵、统计检验、基尼指数、粗糙集理论四个方面[5-6]。其中，CHAID（Chi-Squared Automatic Interaction Detector）是Kass等人于1980年提出的决策树算法[7]，具有数据类型适用范围广、可建立多叉树、从统计显著性检验角度确定最佳分割变量的优点，已经被广泛用于许多分类和回归应用。却存在容易过拟合的缺点。目前，CHAID方法在社会调查[8]、市场研究[9]、医学[10]等领域广泛应用。车敏诗等[11]提出一种基于混沌特征及优化CHAID决策树的情绪识别方法，优化后的CHAID决策树的情绪识别率和结果置信度等各项指标明显高于优化前的CHAID决策树。高多多等[12]人运用CHAID方法分析某县农村居民生活方式的影响因素。杨友星[13]对CHAID算法进行了改进，提出了一种使自变量间交互作用较为公平的FCHAID算法，并应用在信用风险分析中。

CHAID算法虽然具有诸多优点，但同其他决策树算法一样易过拟合。随机森林作为一种主流的集成学习算法，因其算法简单、泛化能力强、抗过拟合能力强等优点[14]。本文为改进CHAID算法的缺点，提出CHAID随机森林算法（CHAID Random Forest， CHAID-RF）。以CHAID决策树作为随机森林的基分类器，采用随机采样、随机选择特征以及集成的策略，生成CHAID-RF。

1 方法介绍

1.1 CHAID决策树

卡方自动交互诊断[7]（Chi-squared Automatic Interaction Detector， CHAID）是一种基于统计学方法的决策树算法。CHAID算法相当于一个逐步的过程：首先，为每个自变量找到最好的分区。然后，对自变量的卡方检验值（分类问题）或F统计量（回归问题）进行比较，选出最佳分割变量。根据最佳分割变量的新区间，对数据进行细分。每一个新区间都被独立地重新分析，以产生进一步的细分。

CHAID决策树的特点有：一是自变量和因变量均可以是分类型或数值型；二是能够建立多叉树；三是从统计显著性检验角度确定最佳分组变量和分割点，考虑了自变量与因变量之间的相关性。但是，CHAID存在易过拟合的问题。

1.2 随机森林

随机森林（Random Forest， RF）是一种基于Bagging理论的集成算法，2001年由Leo Breiman提出[15]。RF的最大特点在于随机选择样本和随机选择特征。首先，随机森林对原始数据采取有放回随机抽样方法产生k个子训练集；然后，对每个训练子集随机抽取若干个（一般为，M为特征总数）特征；最后，构建k棵决策树形成随机森林。

经典随机森林的基分类器是分类回归树（Classification and Regression Tree， CART），随机选择样本和随机选择特征弥补了单棵决策树不稳定和容易过拟合的2个主要缺点。因此，RF具有预测准确率高、泛化性强、训练速度快等优点。但在处理不平衡数据时，随机森林模型的性能会大幅度下降。

1.3 CHAID-RF模型

1.3.1 CHAID-RF模型理论分析

CART决策树是随机森林最常用的基分类器，分类和回归任务均能实现，是典型的二叉树。在处理二分类问题中，CART决策树具有较好的分类性能，但在处理多分类问题中，CART决策树的结构会变得复杂。因为，CART决策树在每次节点分割时，只能二分化，把多分类问题转化成多个二分类问题解决，树的深度会增大。

CHAID决策树是一种数据应用范围较广的多叉树，与CART算法的显著区别在于，其最佳分组变量的是当前与输出变量相关性最大的输入变量，而不是使输出变量取值的差异性下降最快的变量。CHAID决策树和其他决策树算法一样，存在泛化能力差的缺陷。采用随机采样和随机选择特征的策略，将CHAID决策树作为基分类器，形成CHAID-RF。CHAID-RF方法保留了CHAID决策树的优点，且解决了单棵决策树的缺陷。CHAID-RF算法思想如下：

输入：训练集D，待测样本

输出：待测样本的类别（输出变量是分类型）或拟合值（输出变量是数值型）

1）采用自助抽样法（Bootstrap）从训练集D中随机抽取k个子训练集，并且每个子训练集的样本量需与原始训练集中样本量保持一致。

2）构建每棵树之前随机抽取特征生成特征子集。

3）运用卡方检验（输出变量是分类型）或方差分析的F检验（输出变量是数值型）得出最佳分裂特征，并生长出子节点。

4）递归循环步骤2至步骤3，直到满足停止条件，决策树构建完毕。

5）集成k棵决策树，形成随机森林。

6）对于待测样本，k棵决策树得出k个结果。

7）对k个结果进行投票（输出变量是分类型）或取平均值（输出变量是数值型）得到结果。

1.3.2 CHAID-RF分类模型

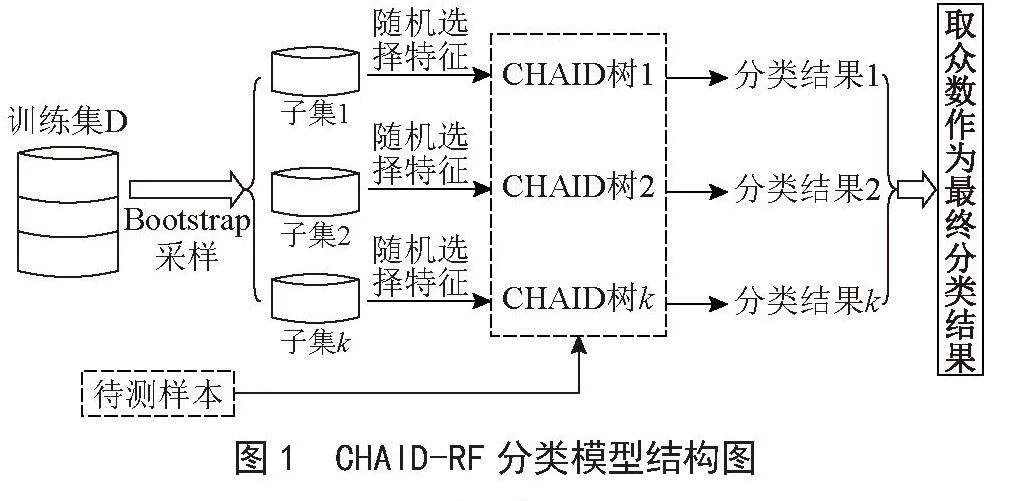
当输出变量是分类型时，CHAID-RF是一个分类模型。分类任务中，每棵CHAID决策树会得到一个分类结果，CHAID-RF将所有决策树分类结果的众数作为待测样本的最终结果。CHAID-RF分类模型结构如图1所示。

1.3.3 CHAID-RF回归模型

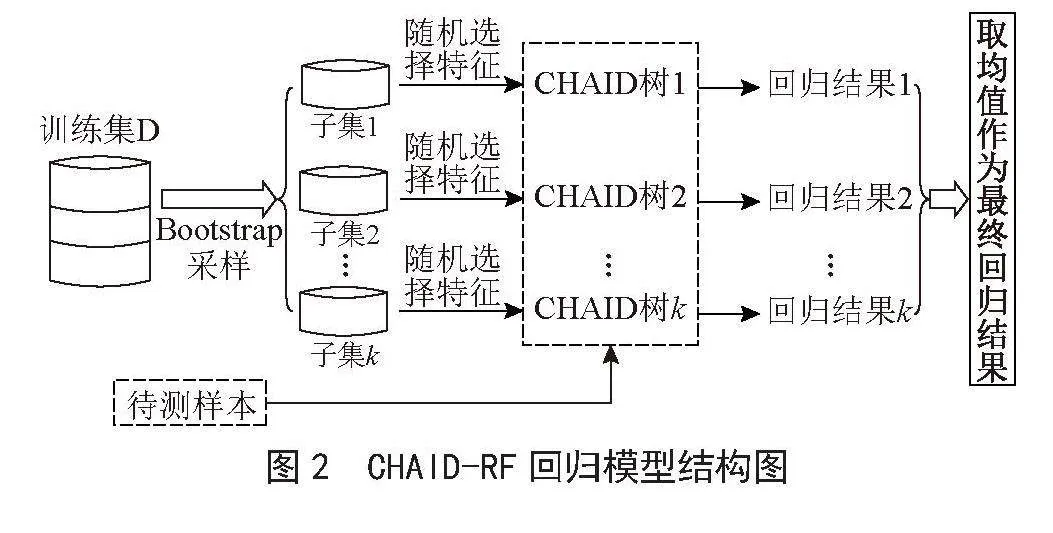
当输出变量是数值型时，CHAID-RF是一个回归模型。回归任务中，每棵CHAID决策树会得到一个回归值，CHAID-RF将所有决策树回归结果取平均作为待测样本的最终结果。CHAID-RF回归模型结构如图2所示。

2 实验结果

2.1 实验数据

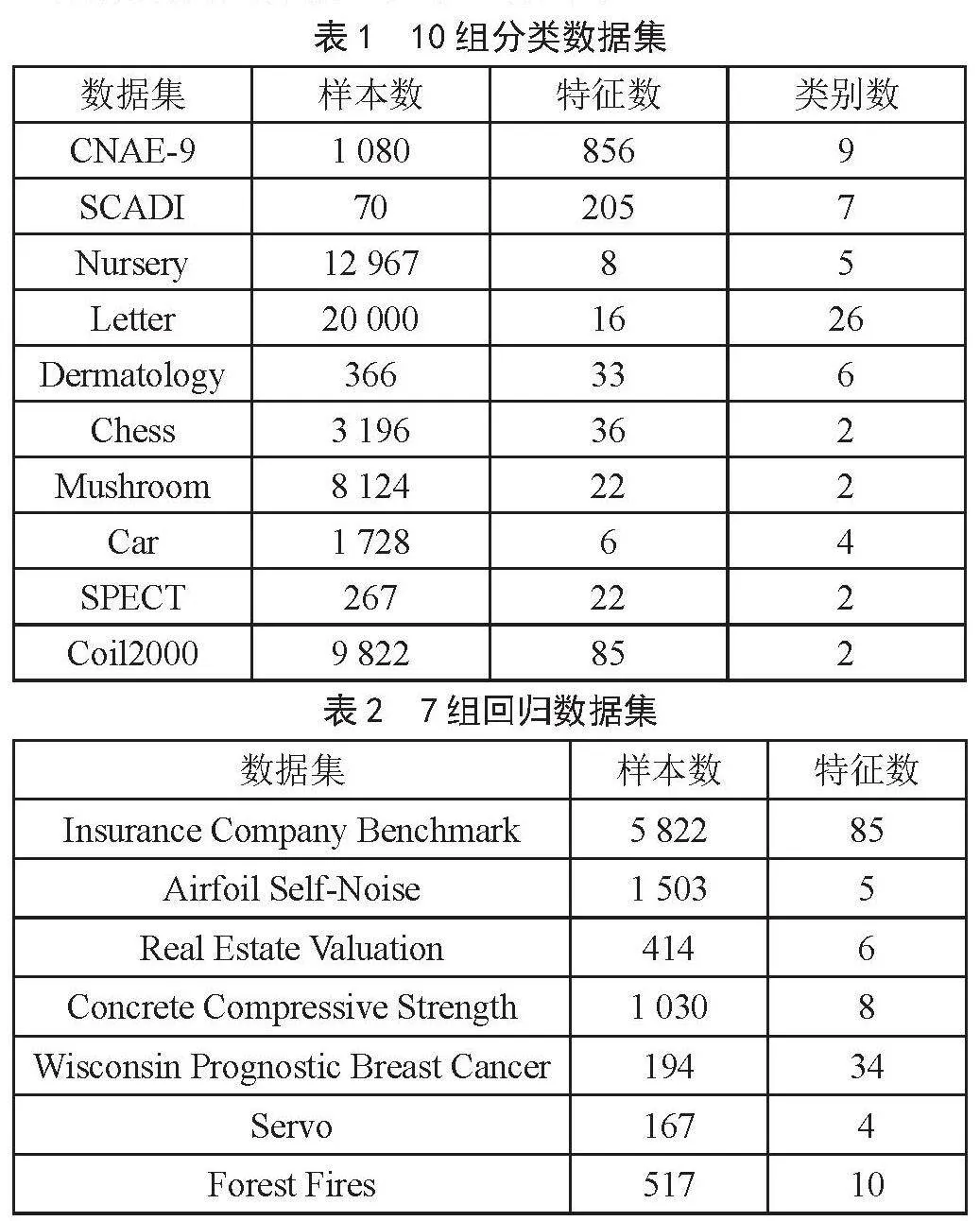
分类任务的10组数据集、回归任务的7组数据集均来自UCI数据库（http：//archive.ics.uci.edu）。10组分类数据集的具体信息如表1所示。回归任务的7组数据集的具体信息如表2所示。

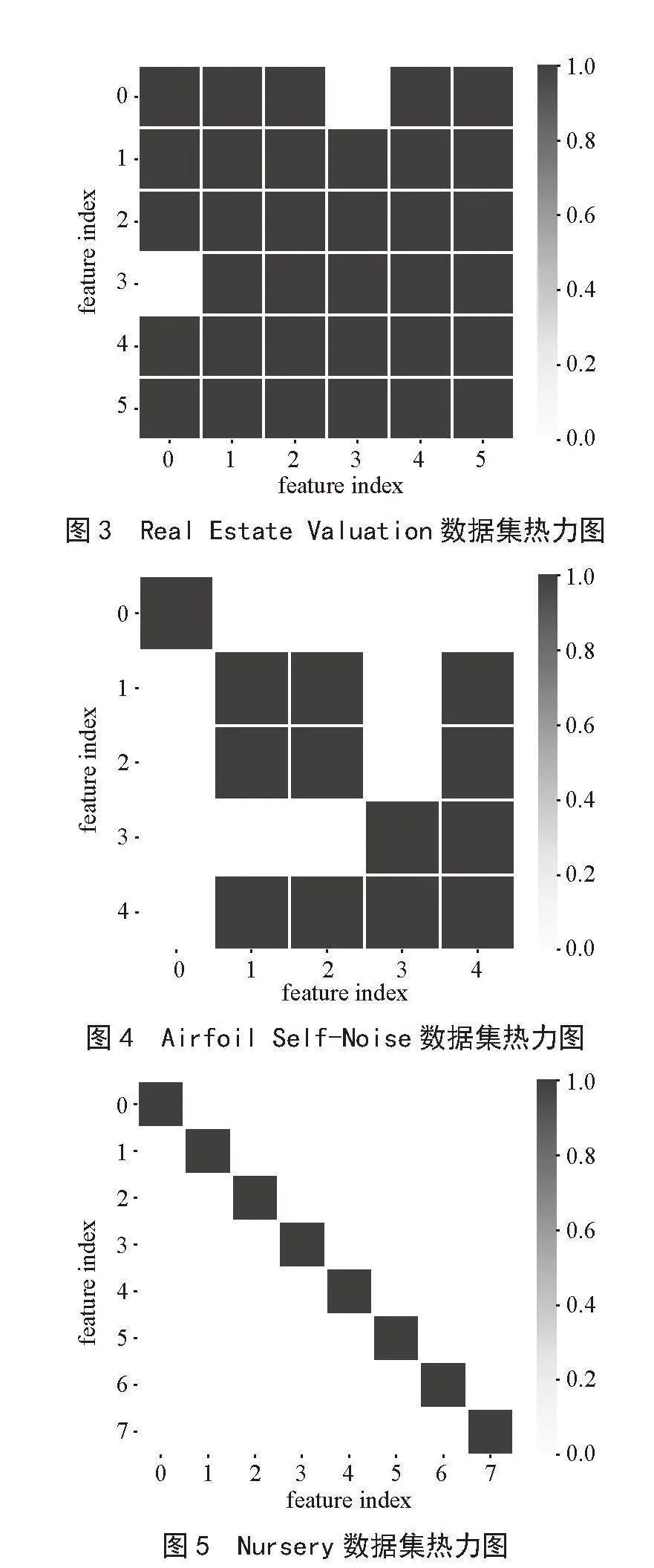
本文通过计算自变量之间的互信息判断其冗余性的大小，并对每个数据集的互信息值做归一化处理，参考相关系数的范围划分，当互信息大于等于0.4时为中度相关或者高度相关，故设互信息阈值为0.4，小于0.4的互信息值以白色覆盖。根据相关结果，将数据分为3类：

1）含有大量冗余变量的数据集：Real Estate Valuation、Concert、Wisconsin Prognostic Breast Cancer、Forest Fires。

2）含有部分冗余变量的数据集：SCADI、Letter、Dermatology、Mushroom、Coil2000、Insurance Company Benchmark、Airfoil Self-Noise。

3）不含或含有极少冗余变量的数据集：CNAE-9、Nursery、Chess、Car、SPECT、Servo。

以下展示了这3类情况中经典数据集归一化后的结果图：其中图3是Real Estate Valuation数据集热力图，图4是Airfoil Self-Noise数据集热力图，图5是Nursery数据集热力图。

2.2 评价指标

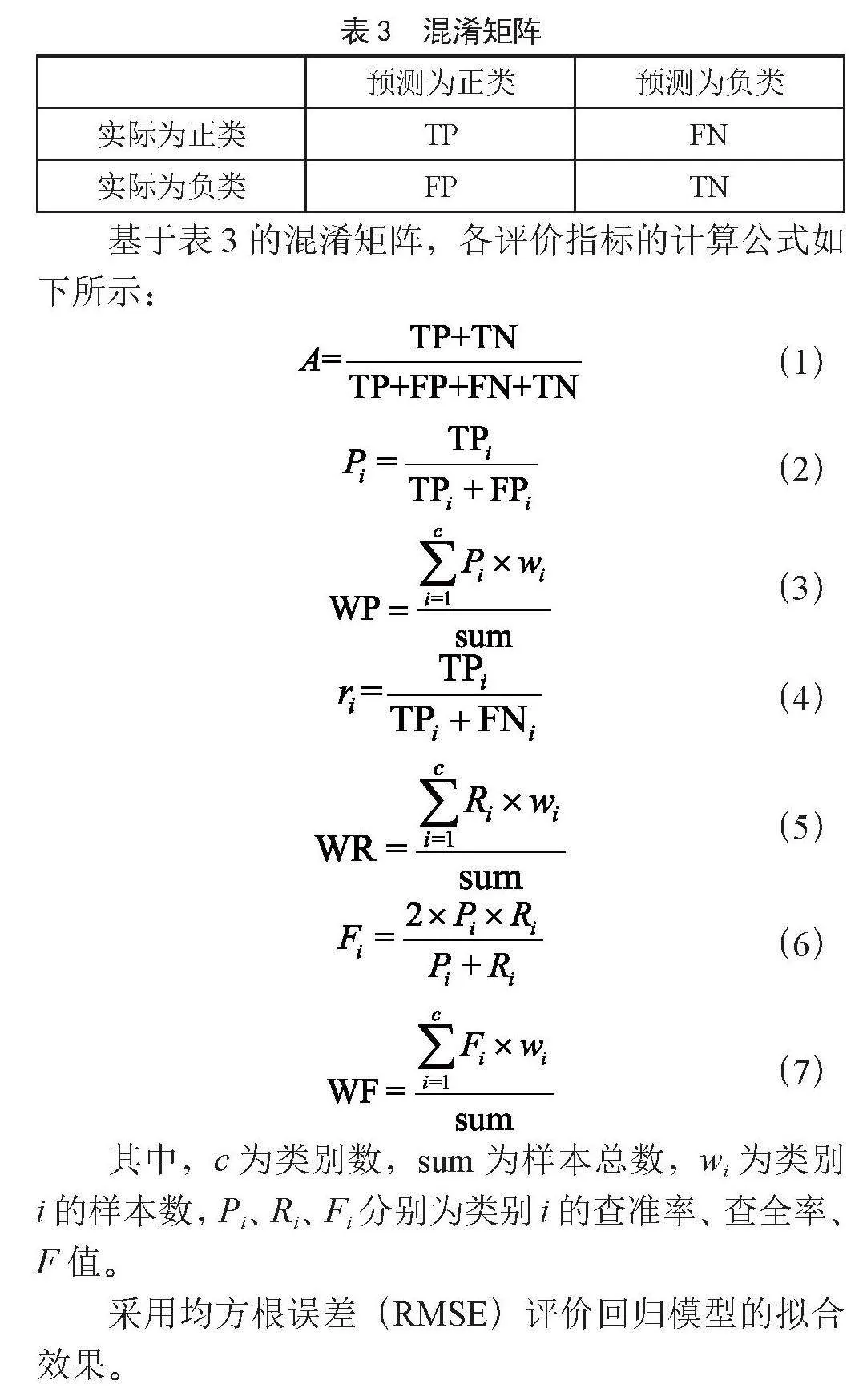
准确率（A）常用于评价分类模型的整体性能，但它在评价不平衡数据集时会对分类结果产生误导。因此，常添加查准率（P）、查全率（R）和F值对算法进行有效验证。然而，查准率、查全率和F值仅适用二分类任务，对多分类任务不再适用，常用的多分类指标有Kappa系数[16]、海明距离[17]、杰卡德相似系数[18]等。为了使评价指标能同时适用于二分类和多分类任务，本文选用加权查准率（Weight Precision， WP）、加权查全率（Weight Recall， WR）和加权F值（Weight F， WF）值将多分类问题转化为多个二分类问题进行评价。为了更直观地给出这些评价指标的计算公式，需要用到的混淆矩阵如表3所示。

基于表3的混淆矩阵，各评价指标的计算公式如下所示：

（1）

（2）

（3）

（4）

（5）

（6）

（7）

其中，c为类别数，sum为样本总数，wi为类别i的样本数，Pi、Ri、Fi分别为类别i的查准率、查全率、F值。

采用均方根误差（RMSE）评价回归模型的拟合效果。

2.3 实验结果和分析

为验证本文提出的CHAID随机森林方法的分类以及回归效果，设置了CART、CHAID、支持向量机（SVM）和随机森林（RF）4种对比算法。本文实验环境为Win 10操作系统（64位）、Intel Core i5-3470 CPU @3.20 GHz、8.00 GB内存，使用Python语言编写算法，IDE为PyCharm 2020.2.3。实验过程中，显著水平a设为0.05，随机抽取的特征数为，父节点样本数最小为2，叶节点样本数最小为1，RF和CHAID-RF中决策树的数量均为100。

2.3.1 分类实验结果与分析

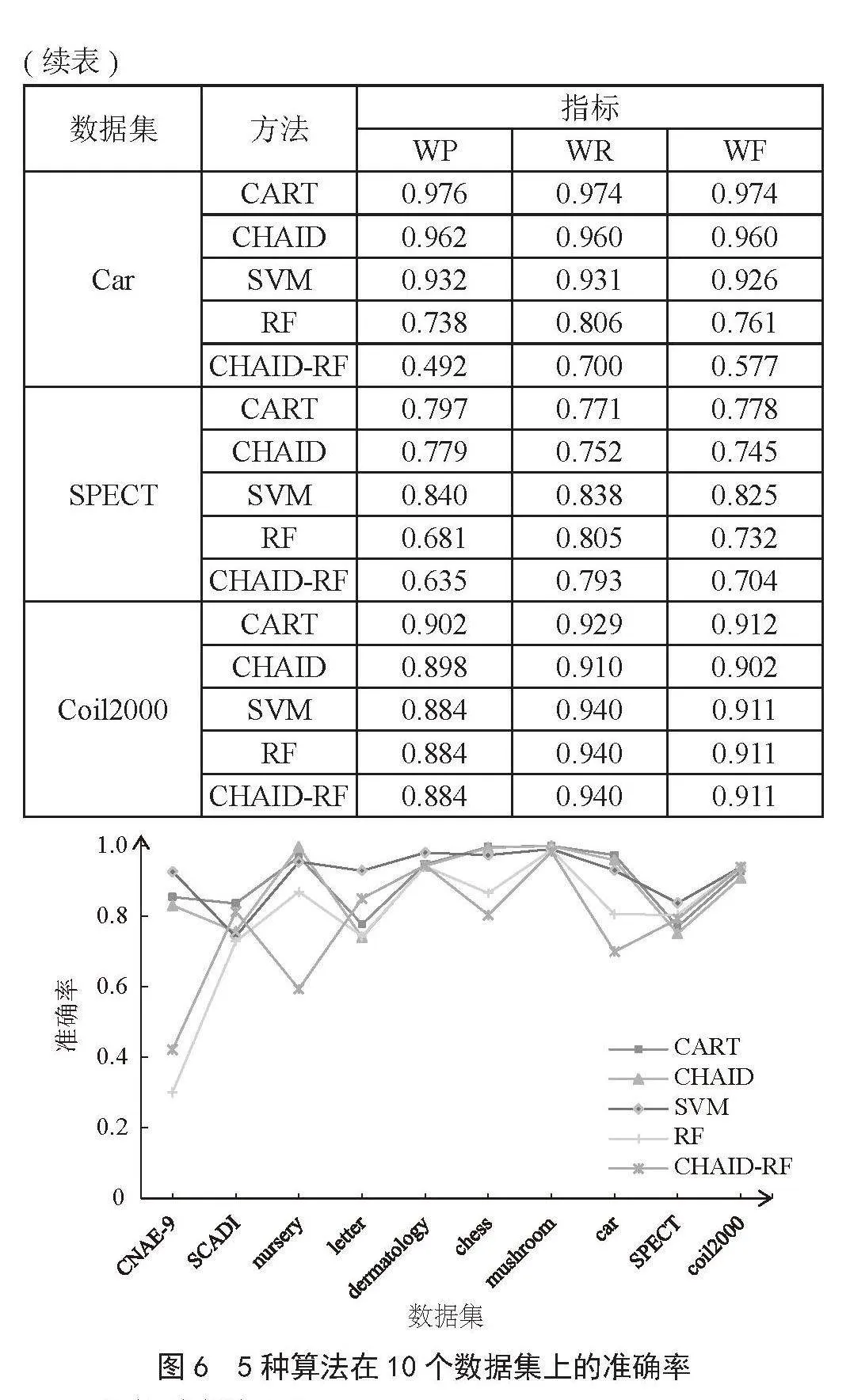
本文通过十组分类数据集，通过十折交叉验证准确率、加权查准率、加权查全率、加权F值，比较CART、CHAID、SVM、RF和CHAID-RF这5种算法的分类性能，实验结果如表4、表5和图6所示。

具体分析如下：

1）5种算法实验结果综合分析。由表4、表5和图6可知：一是Coil2000数据集上，SVM、RF、CHAID-RF这3种方法的4种评价指标结果相同，但加权查准率、加权查全率、加权F值低于CART决策树的结果。Coil2000数据集大类含9 236个样本，小类仅含586个样本，因此，该结果可能是Coil2000数据集类别不平衡导致的。二是SVM算法在数据集CNAE-9、Letter、Dermatology、SPECT的4种评价指标结果均优于其他算法，原因可能是SVM适用于小样本学习，并且它的最终分类结果由少量支持向量决定，对异常值不敏感，具有较好的鲁棒性。三是SCADI、Chess、Car数据集上CART方法的分类效果最佳，Mushroom数据集中CHAID和CART方法的分类准确率都是1，Nursery数据集中CHAID方法分类性能最佳。

2）CHAID-RF与CHAID实验结果分析。由表4、表5和图6可知，CHAID-RF算法在Letter数据集中的分类性能高于CHAID。CHAID-RF和CHAID算法在SCADI、Dermatology、SPECT、Coil2000数据集中分类性能相近。CHAID算法在CNAE-9、Nursery、Chess、Mushroom、Car这5个数据集中分类性能更佳。结合数据集的特点分析发现：当数据集中含有部分或大量冗余变量，且自变量的数量较多时，CHAID-RF算法的分类效果和CHAID算法差不多，甚至优于CHAID算法。

3）CHAID-RF与RF实验结果分析。由表4、表5和图6可知，CHAID-RF算法在数据集CNAE-9、SCADI、Letter的4种评价指标均高于RF算法。CHAID-RF和RF算法在Dermatology、Mushroom、Coil2000中的4种评价指标结果相近。CHAID-RF算法在数据集Nursery、Chess、SPECT的4种评价指标均低于RF算法。

综上所述，本文提出的CHAID-RF算法具有较好的分类效果，CHAID-RF在CNAE-9、SCADI、Letter这3个多分类数据集上分类效果也优于传统随机森林。

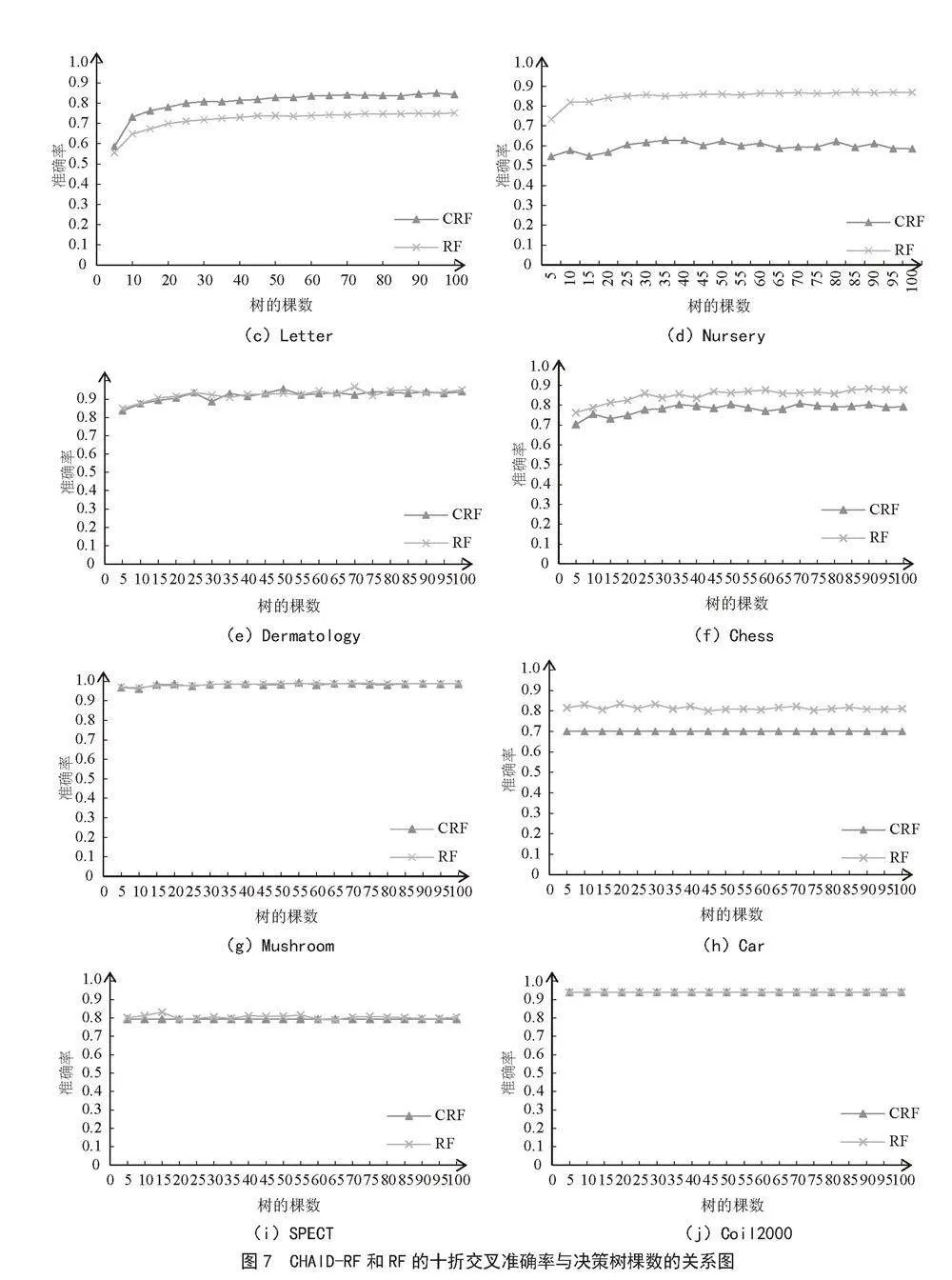
4）稳定性分析。为了探究子决策树规模对CHAID-RF算法性能的影响，进行稳定性对比实验。本文设定森林中初始决策树的棵数为5，步长为5，依次递增直到100棵决策树为止。以十折交叉验证的准确率为评价指标，将本文提出的CHAID-RF算法和RF算法的实验结果进行对比，在10组分类数据集的实验结果如图7所示。

图7中有10张子图，每张子图代表一个数据集的CHAID-RF和RF的十折交叉准确率与决策树棵数的变化关系。其中，横坐标代表树的棵数，纵坐标代表十折交叉准确率。由图7分析可知：

1）随决策树的棵数的增加，CHAID-RF和RF的十折交叉准确率有上升趋势，当树的棵数达100时，10组数据集的十折交叉验证准确率都稳定。

2）在CNAE-9、SCADI、Letter这3个数据集中CHAID-RF算法的分类准确率明显优于RF。

3）CHAID-RF与RF的收敛速度相近。

2.3.2 回归实验结果与分析

本文通过7组回归数据集，通过十折交叉验证RMSE，比较CART、CHAID、SVM、RF和CHAID-RF这5种算法的回归性能，实验结果如表6所示。

具体分析如下：

1）5种算法实验结果综合分析。由表6可知，CHAID-RF在数据集Insurance Company Benchmark、Wisconsin Prognostic Breast Cancer上的均方根误差最小；RF在数据集Real Estate Valuation的均方根误差小于其他算法；SVM在数据集Forest Fires的均方根误差最小；CART在数据集Airfoil Self-Noise、Concrete Compressive Strength、Servo的均方根误差最小。

2）CHAID-RF与CHAID实验结果分析。由表6可知，Insurance Company Benchmark、Airfoil Self-Noise、Real Estate Valuation、Concrete Compressive Strength、Wisconsin Prognostic Breast Cancer、Forest Fires这6个数据集中CHAID-RF的均方根误差小于CHAID。Servo数据集中CHAID的均方根误差小于CHAID-RF，可能是Servo数据集的特征个数太少，造成CHAID-RF的单棵决策树在建立过程中学习内容不足，进而影响CHAID-RF的回归效果。结合数据集的特点分析发现：当数据集中含有部分或大量冗余变量且自变量的数量较多时，CHAID-RF算法的拟合效果优于CHAID算法。

3）CHAID-RF与RF实验结果分析。由表6可知，Insurance Company Benchmark、Wisconsin Prognostic Breast Cancer、Forest Fires这3个数据集中CHAID-RF的均方根误差小于RF。Airfoil Self-Noise、Real Estate Valuation、Concrete Compressive Strength、Servo这4个数据集中RF的均方根误差小于CHAID-RF。实验结果表明，CHAID-RF同RF一样可用于回归分析，并且在某些数据集中CHAID-RF拟合效果优于RF。

综上所述，本文提出的CHAID-RF算法亦可实现回归任务，并且在Insurance Company Benchmark、Wisconsin Prognostic Breast Cancer数据集上拟合效果最优。

4）稳定性分析。为了探究子决策树规模对CHAID-RF算法性能的影响，进行稳定性对比实验。本文设定森林中初始决策树的棵数为5，步长为5，依次递增直到100棵决策树为止。以十折交叉验证的RMSE为评价指标，将本文提出的CHAID-RF算法和RF算法的实验结果进行对比，在7组分类数据集的实验结果如图8所示。

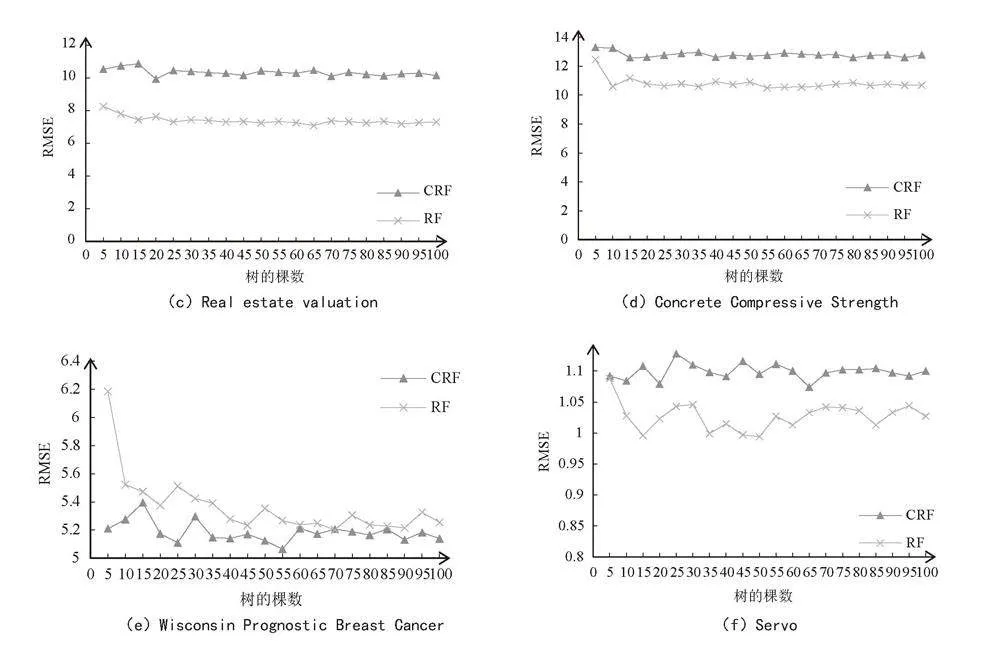
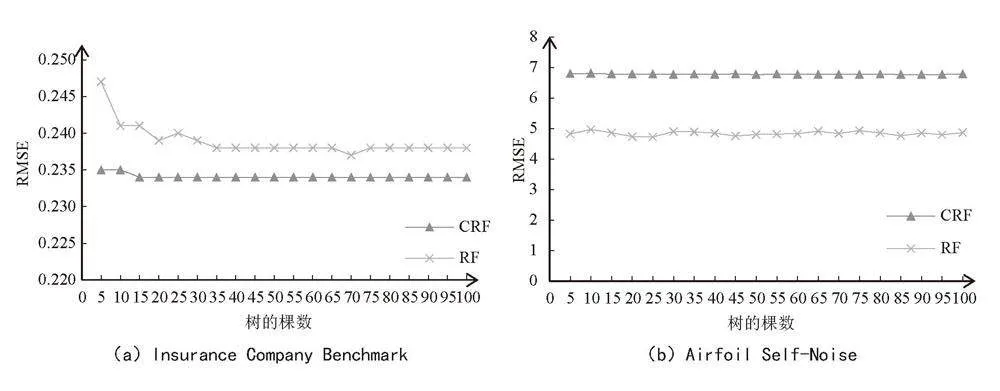
图8中有7张子图，每张子图代表一个数据集的CHAID-RF和RF的十折交叉RMSE与决策树棵数的变化关系。其中，横坐标代表树的棵数，纵坐标代表十折交叉RMSE。图8分析可知：

1）随决策树的棵数的增加，CHAID-RF和RF的十折交叉RMSE有下降趋势，当树的棵数达100时，7组数据集的十折交叉验证RMSE均稳定。

2）在数据集Insurance Company Benchmark、Wisconsin Prognostic Breast Cancer、Forest Fires这3个数据集CHAID-RF算法的拟合效果优于RF。

3）CHAID-RF与RF的收敛速度相近。

3 结 论

针对CHAID算法容易过拟合的缺陷，本文提出CHAID-RF算法。CHAID-RF方法的基分类器是CHAID决策树，当CHAID决策树规模达到一定数量后，CHAID-RF的评价指标保持在稳定的范围内。通过10个分类数据集和7个回归数据集实验，实验结果表明，CHAID随机森林方法具有较好的分类和回归效果。但是，本文提出的CHAID-RF算法在样本不平衡的数据中的结果会偏向于训练集中样本量多的类别，在后期工作中，将进一步深入研究。

参考文献：

[1] LAWRENCE R L，WRIGHT A. Rule-Based Classification Systems Using Classification and Regression Tree （CART） Analysis [J].Photogrammetric Engineering and Remote Sensing，2001，67（10）：1137-1142.

[2] 谢鑫，张贤勇，杨霁琳.融合信息增益与基尼指数的决策树算法 [J].计算机工程与应用，2022，58（10）：139-144.

[3] 王川杭.消除随机一致性的决策树及深度森林方法 [D].太原：山西大学，2021.

[4] HAYES T，USAMI S，JACOBUCCI R，et al. Using Classification and Regression Trees （CART） and Random Forests to Analyze Attrition： Results from Two Simulations [J].Psychology and Aging，2015，30（4）：911-929.

[5] CAMPBELL P R J，FATHULLA H，AHMED F. FuzzyCART： A Novel Fuzzy Logic based Classification & Regression Trees Algorithm [C]//2009 International Conference on Innovations in Information Technology （IIT）.Al Ain：IEEE，2009：175-179.

[6] 姚岳松，张贤勇，陈帅，等.基于属性纯度的决策树归纳算法 [J].计算机工程与设计，2021，42（1）：142-149.

[7] 薛薇，陈欢歌.SPSS Modeler数据挖掘方法及应用：第2版 [M].北京：电子工业出版社，2014.

[8] 程国柱，程瑞，徐亮.公路小半径曲线段外侧车道路侧事故概率预测 [J].哈尔滨工业大学学报，2021，53（3）：178-185.

[9] 程可.基于CHAID模型的P2P网贷平台财务预警研究 [D].太原：山西财经大学，2018.

[10] 赵巧燕，浮志坤，陈健超，等.冠状动脉搭桥术后医院感染风险预测模型构建 [J].中华医院感染学杂志，2021，31（2）：296-300.

[11] 车敏诗，聂春燕，范如俊，等.一种基于混沌特征及优化CHAID决策树的情绪识别方法 [J].计算机应用研究，2020，37（S2）：105-107.

[12] 高多多，张爱莲，任雯娟.基于CHAID模型的某县农村居民生活方式影响因素分析 [J].中国卫生统计，2020，37（5）：659-663.

[13] 杨友星.CHAID算法并行化及其在信用风险分析中的应用 [D].长春：长春工业大学，2016.

[14] 徐精诚，陈学斌，董燕灵，等.融合特征选择的随机森林DDoS攻击检测 [J].计算机应用，2023，43（11）：3497-3503.

[15]陈志添.基于决策树的诊断相关组分类研究 [D].广州：华南理工大学，2018.

[16]徐树良，王俊红.基于Kappa系数的数据流分类算法 [J].计算机科学，2016，43（12）：173-178.

[17]谭吉玉，朱传喜，张小芝，等.基于海明距离和TOPSIS的直觉模糊数排序法 [J].统计与决策，2015（19）：94-96.

[18]于海平，林晓丽.基于增强双边滤波的图像分割模型及应用 [J].计算机工程与设计，2019，40（4）：1064-1069.

作者简介：聂斌（1972—），男，汉族，江西吉安人，教授，研究生导师，CCF会员，博士研究生在读，研究方向：数据挖掘、中医药信息学、中药学；靳海科（1999—），女，汉族，山西晋城人，硕士研究生在读，研究方向：数据挖掘；李欢（1995—），女，汉族，江西萍乡人，助教，硕士研究生，研究方向：数据挖掘；陈裕凤（1996—），女，汉族，江西南昌人，助教，硕士研究生，研究方向：数据挖掘；张玉超（1998—），男，汉族，重庆垫江人，硕士研究生在读，研究方向：数据挖掘；郑学鹏（1997—），男，汉族，广东汕尾人，硕士研究生在读，研究方向：数据挖掘。

收稿日期：2024-03-04

DOI：10.19850/j.cnki.2096-4706.2024.17.007

基金项目：国家自然科学基金项目（82260849，61562045）；江西省教育厅科技计划研究项目（GJJ211256）；江西中医药大学校级科技创新团队发展计划（CXTD22015）

CHAID-RF： Ensemble Learning Method Based on CHAID Decision Tree

NIE Bin， JIN Haike， LI Huan， CHEN Yufeng， ZHANG Yuchao， ZHENG Xuepeng

（College of Computer Science， Jiangxi University of Chinese Medicine， Nanchang 330004， China）

Abstract： Aiming at the problem that CHAID Decision Tree is easy to overfitting， CHAID-RF is proposed. In this method， CHAID Decision Tree is used as the base classification to form CHAID-RF by random sampling， random feature selection and integration strategies. CART， CHAID， SVM， and RF are selected as the comparison algorithm to verify the effectiveness of CHAID-RF， accuracy， Weighted Precision Ratio， Weighted Recall Ratio， and Weighted F-measure are used as evaluation index of classification model， and Root Mean Square Error is used as evaluation index of regression model， 10 classification data sets and 7 regression data sets are used for validation. The experimental results show that CHAID-RF is feasible and effective.

Keywords： CHAID; Random Forest; CHAID-RF; classification; regression