流转约束下的预制构件生产排程优化研究

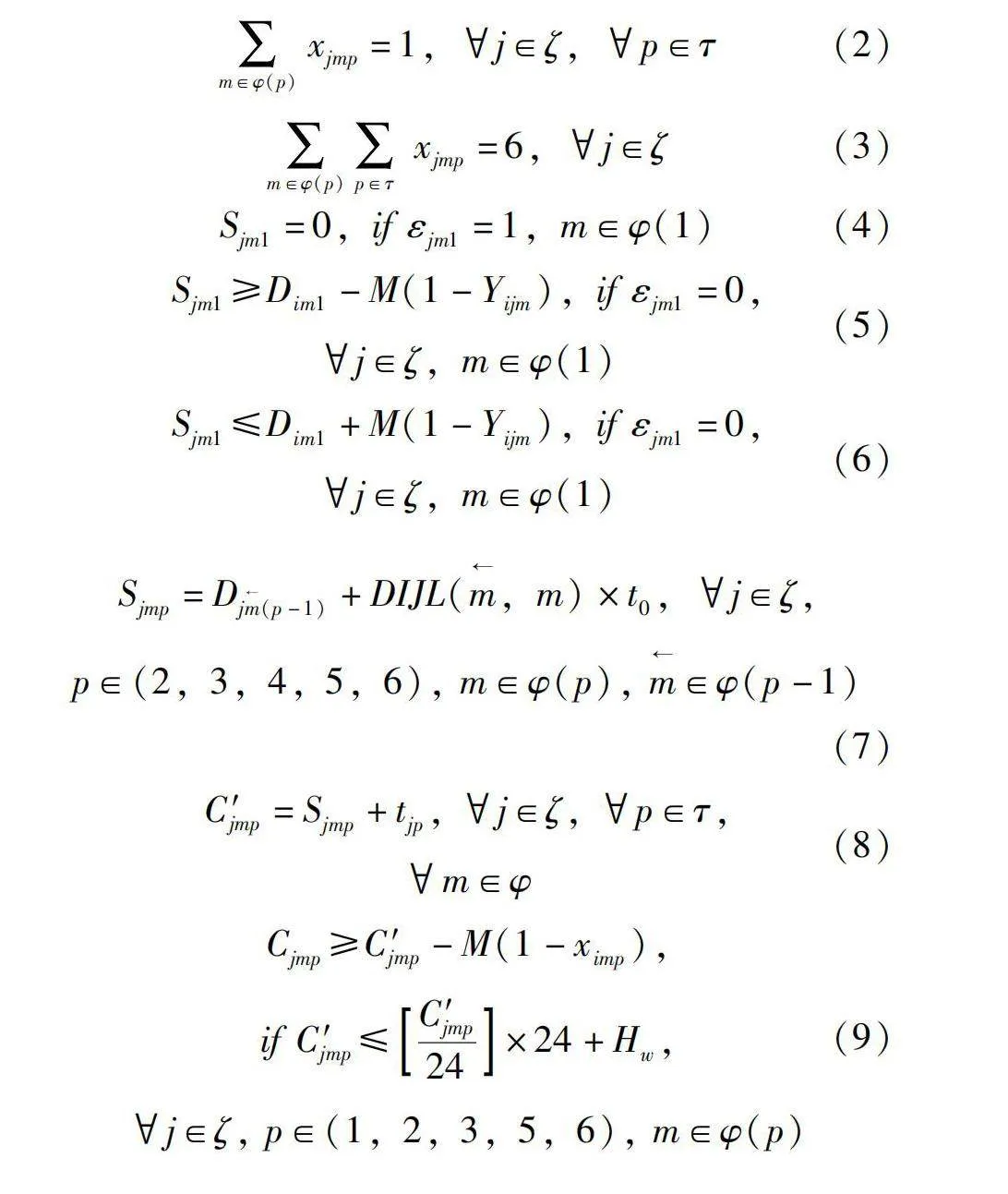
摘要：针对装配式建筑预制构件生产过程中存在的流转约束问题，通过分析梁场生产线布局特点，考虑到工序之间的流转约束及工位资源利用情况，以最小化最大完工时间为目标，建立预制构件生产调度模型，采用遗传算法求解模型得到预制构件最佳生产方案。结果表明，该模型算法得出的生产方案相比传统调度方法的日均生产效率提高15.2%，较大地提高预制构件生产效率和工程进度控制。

关键词：预制构件；生产调度；流转约束；遗传算法

0 引言

与传统现浇筑建筑相比，装配式建筑具有施工效率高、质量稳定及减少环境污染等诸多优点。装配式建筑通过将所需的结构构件统一在预制场中生产并运输到现场中拼装，从而有效地减少了施工现场对空间和时间的要求，提高了工程质量和进度控制的可靠性。在国家政策的大力支持下，《关于推动智能建造与建筑工业化协同发展的指导意见》等文件明确提出了推动建筑业向标准化、工业化和集约化的产业生产模式转型的目标。在此背景下，装配式建筑迅速崛起并得到广泛应用。

然而，预制构件作为装配式建筑的核心组件，其生产调度效率直接影响着装配式建筑的建造进度和成本。传统生产排程通常依赖于人工经验和简单的调度规则，难以获得最优的生产排程计划，容易导致工序相互阻塞，从而造成产能损失。针对这一问题，学者们展开了丰富的研究。徐洁等^[1]基于JIT理论提出了一种多资源、多目标的快速排程算法，通过资源占用判断、冲突处理与自动调整实现了桥梁预制梁场的快速生产排程。秦旋等^[2]考虑了预制构件生产过程中的资源约束，建立了以生产完工时间和惩罚成本为目标的多目标预制构件生产调度模型，并采用改进的共生生物搜索算法进行优化求解。Dan等^[3]从工序约束角度提出了一种预制构件生产调度优化模型，考虑了工艺连接和阻塞。此外，基于预制构件的生产工序及资源约束情况，于淼等^[4]对预制构件生产的鲁棒性调度问题进行了研究，建立了以预制构件生产完工时间最短和鲁棒值最大为目标函数的双层规划模型。同时，部分研究关注于预制构件生产的动态调度，探索了运营不确定性下的调度及由于需求变化而重新调度的问题^[5-6]。Kim等^[7]将建筑施工进度的不确定性纳入预制构件生产调度模型中，提出了一种动态调度模型，能够实时响应到期日期变化，并最大限度地减少延误。类似地，Du等^[8]研究了预制工厂内部因素引起的生产延误和外部因素引起的需求变化下的动态调度。在模型求解算法方面，遗传算法^[9-10]、NSGA-Ⅲ算法^[11]、模拟退火^[12]等启发式算法被广泛使用，以实现多目标优化和高效的求解过程。例如，汪和平等^[13]构建了多流水线构件混合生产的调度模型，综合考虑了车间调度的模具资源配置、构件生产顺序、构件在流水线的变化程度、生产成本、生产工期和生产能耗等多维度的目标优化，并采用改进种群初始化的NSGA-Ⅲ算法对模型进行求解。

然而，以上研究虽考虑了预制构件生成中的资源约束、不确定因素约束等问题，但较少考虑生产线布局带来的流转约束问题，在实际生成中，为了节约用地成本和提高使用效率，预制场被设计成非直线型流水线，其中流转工位可用于加工多个不同工序，实现生产工序路线闭环，从而提高工位的使用效率。然而，这种布局方式也带来了流转约束问题，即当某构件在流转工位长时间加工时，会导致后续构件必须在工位上等待，甚至出现前序构件无法释放当前工位的情况。这种阻塞传递会导致整个预制流水线的生产瓶颈问题，影响整体生产效率和工程进度。

因此，本文基于工位流转约束条件对预制构件生产排程问题进行研究，结合实际生产线布局问题带来的流转约束进行排程模型建模，并采用遗传算法求解，以实现生产排程优化方案切实应用到实际生产线中。

1 流程流转约束下的预制构件生产排程优化模型

1.1 基于流转约束的预制构件生成调度描述

梁场生产线布局如图1所示，其中包含一条环形生产线，由7个工位、6个胎膜架和4个蒸养室组成，工位和蒸养室间铺设有轨道供台车，按照预定的轨迹转移。该生产线生产预制构件的过程包含6道工序，分别是：钢筋绑扎（工序1）、预埋件安装（工序2）、模板安装（工序3）、混凝土浇筑（工序4）、蒸养（工序5）、脱膜修整（工序6），其中工序1是在胎膜架上完成，不参与流水线流转过程，同时由于构件工艺约束，工序4（混凝土浇筑）和工序5（蒸养）之间不允许存在时间间隔，否则会影响混凝土的强度。各工序与工位的对应关系见表1。

生产线存在以下流转约束问题：

（1）1号工位为生产线的核心流转工位。当1号工位被占用时（工序4、6），会存在潜在的冲突问题。一方面，若蒸养室全部占用，蒸养室无法释放已完成蒸养的预制构件，并且完成工序4的构件也无法进入蒸养室，从而可能导致整条流水线的锁死问题；另一方面，不合适的1号工位的工序安排，会影响3、5、6、7号工位的构件工序加工状态，通过逐个工位的传递，造成整个生产线的阻塞蔓延，严重影响生产效率和进度控制。

（2）工序3和6均可选择

多个工位进行加工，但它们并非是并行的过程。例如，若当前构件选择在3号工位进行工序3的加工，则后续构件将无法进入5、6、7号工位进行工序3的加工。这种情况下，未能合理利用其他工位的资源，可能导致某些工位闲置和生产效率下降。

（3）由于工序4和工序5之间存在过程连接，因此从工序3的工位到工序4的工位流转受蒸养室工位占用情况的影响。

1.2 数学模型构建

基于实际非线性生产线布局带来的流转约束进行建模是将调度优化方法应用到实际生产线的关键，但这也增加了建模的复杂性和求解的难度。对此，本文做出以下基本假设：

（1）不考虑台座和施工工人资源数量的限制。

（2）工序按照先到先加工原则进行加工。

（3）初始时刻，所有工作站、设备、工人都处于可用状态。

（4）龙门吊吊装时间计入到工序2中，台座在相邻工位间的移动算一次转移，每次转移时间相同。

（5）一个工作日被划分为正常工作时间、加班时间和非工作时间。

模型使用的符号及其含义见表2。

1.2.1 目标函数

预制构件生成排程优化的目标是提高生产效率，以确保每天生产的预制构件数量最大化。这一目标可以转换为尽可能缩短完成最后一个预制构件的最后一道工序的时间，以提高整个批次的生产效率。对此，本文将最小化预制构件的最大完工时间作为目标函数公式如下

minC=maxD_jm6（1）

1.2.2 约束条件

约束（2）保证预制构件的每道工序只能在一个工位上完成；约束（3）表示预制构件的6道工序均要完成；约束（4）定义当预制梁是加工工序1的工位中的首个加工工件时，则初始化其工序开始时间；约束（5）和（6）确保了在前一工件i完成后，后续工件j在工位m上加工工序1的开始时间；约束（7）为工件j从上一工位m←转移到下一工位m后进行工序p加工的开始时间。其中，

DIJL（m←，m）表示从工位

m←到工位m的转移次数，采用Dijkstra算法计算；约束（8）为工件j在工位m上完成工序p的预计完工时间；约束（9）和（10）为工件j在工位m上完成工序p={1，2，3，4，6}的实际完工时间。若在工作日内完成时，实际完工时间等于预计完工时间；约束（11）和（12）确定了工件j完成可中断工序p={1，2，6}时的实际完工时间。若工序工作无法在工作时间段内完成，则将工件当日未完成的剩余加工工作移至第二天完成；约束（13）和（14）确保了对于不可中断工序p=5，工序加工可以在非工作时间内完成；约束（15）表示工序4和工序5的过程连接约束；约束（16）计算工件j在完成工序p={1，2，5}后的预估离开工位时间，min（DIJT（m，m→））表示从m到下一工位m→）的转移路径畅通的最小时间，由Dijkstra算法计算；约束（17）和（18）表示工序3受工序4的流转约束，min（T_φ（5））表示蒸养室最早空闲开放时间。其中约束（17）表示当构件下一工序4能在加班时间前完成时，工件离开工序3工位的时间不能早于蒸养室最早空闲开放时间、转移路径最早通常时间和工序3实际完工时间。约束（18）考虑当件下一工序4不能在加班时间前完成时，则工件完成工序3后应在工位上停留至第二天工作日后，以保证工序4和工序5的过程连接。

2 遗传算法设计

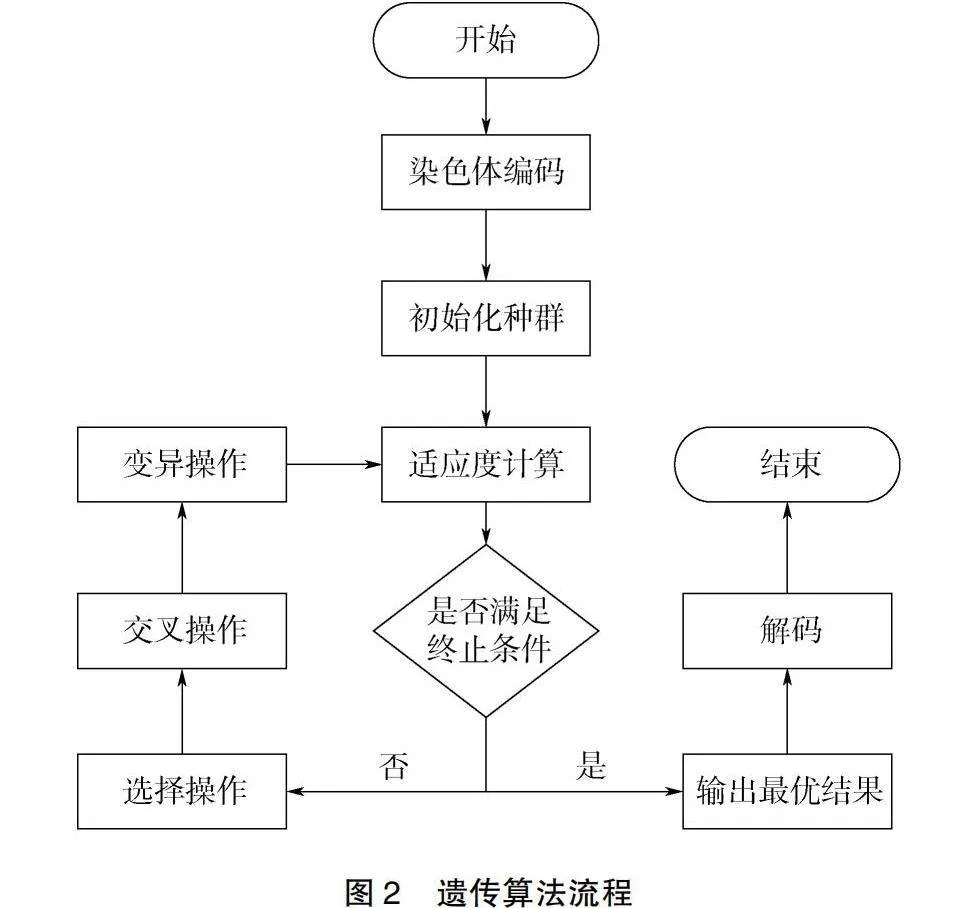
由于梁场为环形单条生产线且相邻工位间不存在缓冲区间，预制构件的加工顺序与进入流水线的次数紧密相关。因此，本文所建立的预制梁生产调度模型在本质上是基于先到先服务（First Come First Service，FCFS）原则进行建模的，即预制梁生产调度优化问题可被视为预制梁生产顺序决策问题，其核心是探索预制梁的最佳生产顺序，以最小化最大完工时间为目标。因此，本文采用改进的遗传算法来优化预制件的生产调度，遗传算法流程如图2示。

2.1 初始种群

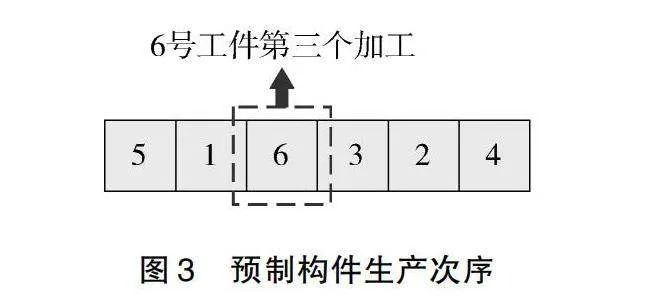
预制构件组生产次序被编码为一个1×n大小的染色体，其中n等于预制构件的总数量。染色体中的每个基因值表示对应的构件索引，而每个基因所在的位置表示对应构件加工的次序。在算法开始时，会随机生成种群数量大小的染色体集合。预制构件生产次序如图3所示。

2.2 计算适应度

采用目标函数（1）的倒数计算染色体的适应度大小。适应度越大的染色体对应的生产序列的最大完工时间越小，因此在后续的迭代进化中，这些染色体越容易被保留下来。

2.3 选择操作

选择操作采用轮盘赌法，从种群中随机选取父染色体，通过后续的交叉和变异操作生成新一代染色体。在轮盘赌法中，染色体所占轮盘的面积与其适应度值成正比，即适应度值越高的染色体在轮盘中被选中的概率越大。

2.4 交叉操作

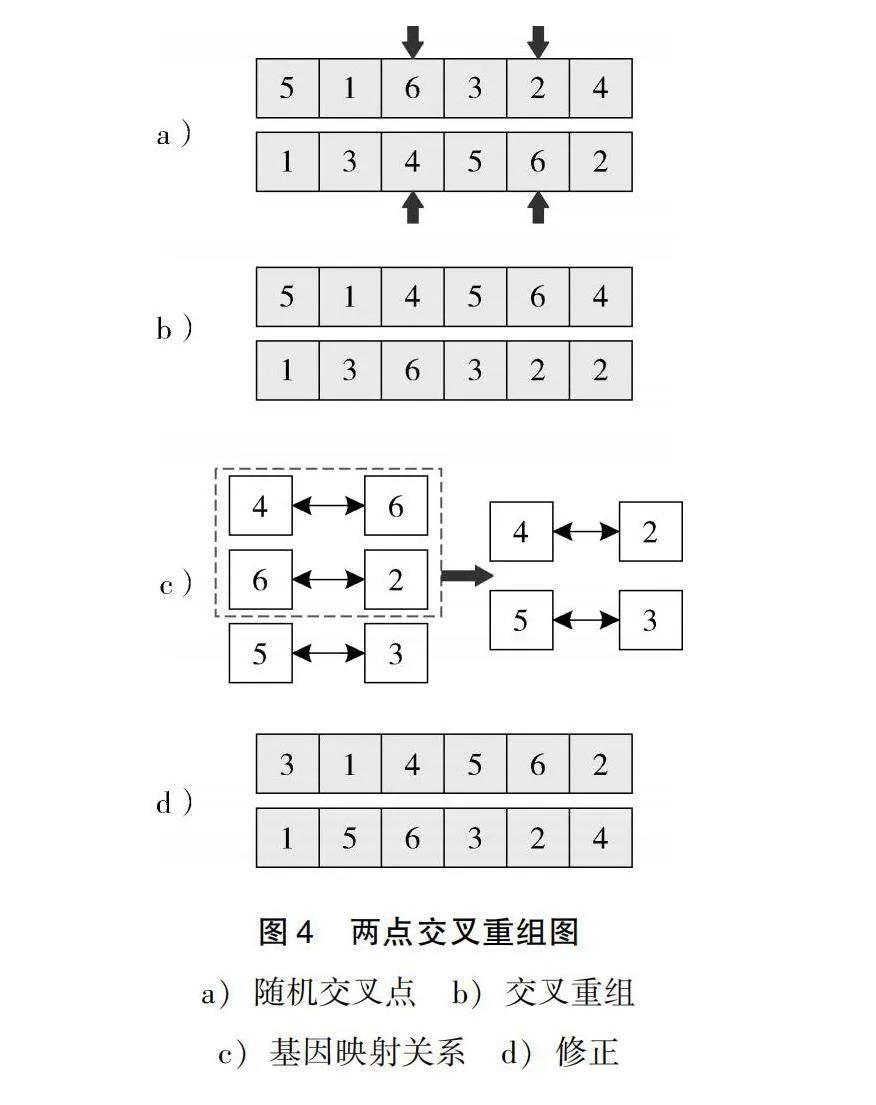
交叉操作通过对选择操作得到的父染色体进行交叉重组，生成新的染色体，以提高算法的搜索能力。本文采用两点交叉法，即随机生成两个小于染色体长度n的随机数k₁和k₂（k₁≤k₂），然后将父染色体在k₁～k₂间的基因进行交叉并重组，两点交叉重组图如图4所示。

然而，通过交叉操作生成的新染色体可能存在基因重复的情况，即生产序列中的部分构件可能替代其他构件进行重复加工，如图4b所示。为解决这一问题，需要将不可行的生产序列修正为可行的生产序列。修正原理是在交叉范围内建立交换基因的映射关系，然后依次对交叉范围外的重复基因进行修正，具体如图4c所示。

2.5 变异操作

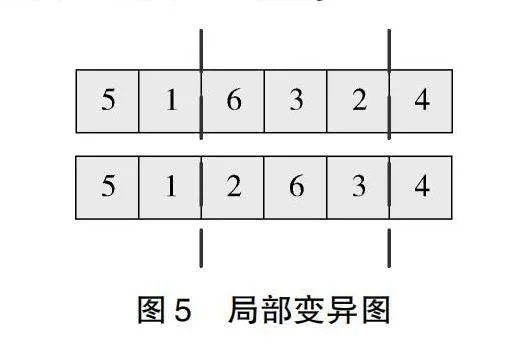
变异操作以较小概率对父染色体的局部基因进行突变，以适当扩大算法搜索空间，从而降低陷入局部最优解的概率。为避免基因重复问题，变异操作采用局部范围变异方法。具体而言，该方法在染色体上随机选择两个点，并将这两点之间的基因重新排列组合。为保证不过度破坏父染色体中的优良基因组合，最多对3个基因进行变异，局部变异图如图5所示。

3 实验分析

3.1 实验准备

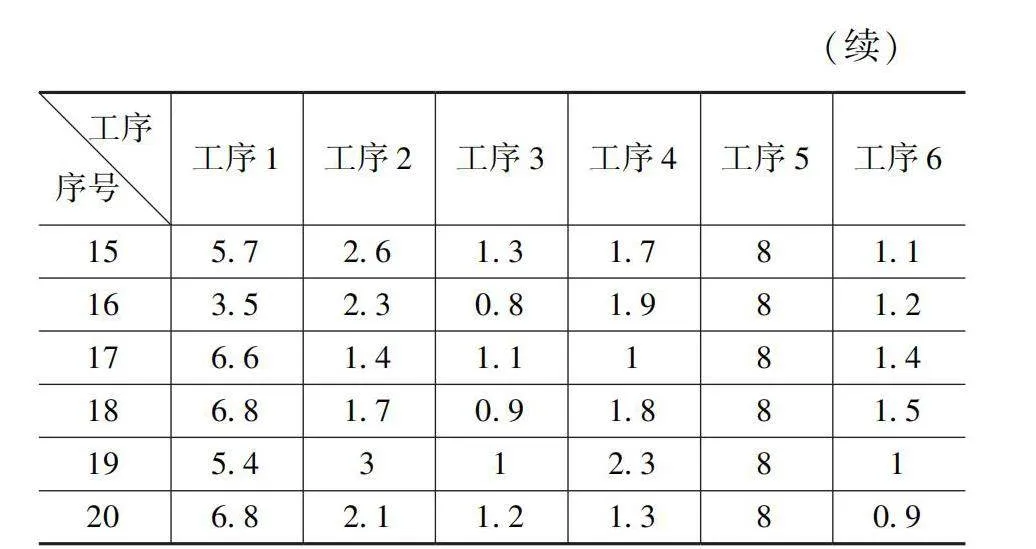
利用实际梁场的实际生产数据对模型和算法进行验证。实验案例共选取20个预制构件，各预制构件的生成信息见表3。正常工作时间为8h/d，允许加班时间为2h，相邻工位转移时间为6min。算法参数设置为：种群规模为50，最大迭代次数为100，交叉概率为0.8，变异概率为0.05。

3.2 仿真分析

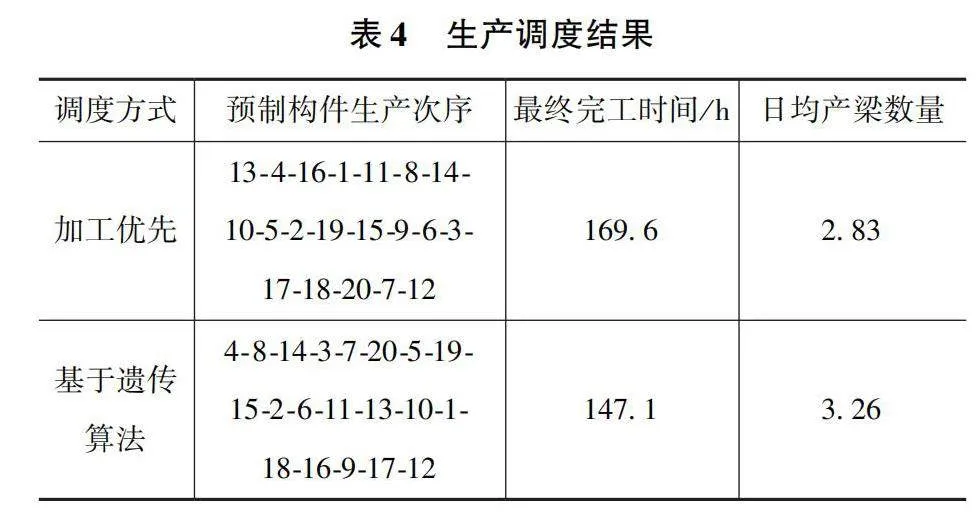
本实验是在pycharm环境中进行的，使用python对数学模型和遗传算法进行编程，得到了20个预制构件的生产调度优化结果，生产调度结果见表4。

通过实验结果可以看出，相较于基于加工优先的传统调度方法，本文所提出的模型和设计算法使得预制构件生产的最大完成时间缩短为147.1h，提前了22.5h，日均生成预制梁的效率提高了15.2%。

为探索不同的预制构件生产顺序对最大完工时间的影响机理，绘制以上两种调度方式的生产甘特图，基于遗传算的调度方案甘特图和基于加工优先原则的调度方案甘特图分别如图6和图7所示。图中，横轴表示时间，初始时间设置为0，粗虚线表示每天正常工作时间范围；细虚线表示每天允许加班时间范围。由纵轴表示1～20构件序号，6个方块表示6道工序加工过程，方块的左端表示工序开始时间，末端表示构件离开工位时间，方块上的数字表示构件所在的工位，其中胎膜架设为零号工位，蒸养室设为八号工位。

由图6和图7可知，基于遗传算法生成的调度方案中，在第一天冷启动过程中，4号和8号工件被合理排序，使得它们都能在第一天完成前5道工序的加工。然而，在基于加工优先原则生成的调度方案中，13号工件第一道工序的启动时间早于4号工件先进入流水线中，由于流转约束，4号工件需要等13号工件的第二道工序加工完成后释放工位才能进入流水线加工第二道工序，从而导致4号工件需要多停留等待2.8h。因此，当天剩余工作时间7.8h只够4号工件完成第二道工序的加工。因此，基于加工优先原则的调度方案在第一天的冷启动阶段整体效率明显低于基于GA生成的调度方案。初期阻塞的影响在后续的加工过程中逐渐传播并积累。第6d（120h～144h），在基于遗传算法生成的调度方案中，除了最后一道工序，剩余构件的其余工序均已完成。而在基于加工优先原则的调度方案中，剩余构件工件7号和12号的浇筑和蒸养等耗时环节尚未开始。直到第7天才对这些工序进行加工，导致整体进程减慢。

4 结语

本文研究了流转约束条件下的预制构件生产调度问题，从生产效率角度考虑，建立了以最小化最大完工时间为目标的生产调度优化模型，并采用遗传算法对模型进行求解。相较于传统调度方法，基于遗传算法得到的优化方案日均生成效率提高了15.2%。同时，通过对比两种调度方案的甘特图，发现基于遗传算法的方案在冷启动条件下的工序安排效率明显优于传统调度方法，有助于更快地达到产能高峰，进而提高整体生产效率。

参考文献

[1]徐洁，章竑骎，刘浩，等.基于JIT理论的桥梁梁场生产排程算法研究[J].建筑经济，2022，43（S2）：239-244.

[2]秦旋，房子涵，张赵鑫.考虑资源约束的预制构件多目标生产调度优化[J].计算机集成制造统，2021，27（8）：2248-2259.

[3]DAN Y R， LIU G W， FU Y. Optimizedflowshop scheduling for precast production considering process connection and blocking[J]. Automatic in Construction， 2021（125）：103575.

[4]于淼， 兰宁， 许音. 不确定环境下预制构件生产鲁棒性调度研究[J]. 沈阳建筑大学学报（社会科学版）， 2024， 26 （1）： 43-49.

[5]WANG Z，HU H，GONG J . Framework for modeling operational uncertainty to optimize offsite production scheduling of precast components[J]. Automatic in Construction， 2018 （86）： 69-80.

[6]LI Z， SHEN G Q.XUE X.Critical review of the research on the management of prefabricated construction[J]. Habitat International， 2014（43）： 240-249.

[7]KIM T，KIM Y，CHO H. Dynamic production scheduling model under due date uncertainty in precast concrete construction[J]. Journal of Cleaner Production， 2020（257）：1-13.

[8] DU J ， DONG P，SUGUMARAN V， et al. Dynamic decision support framework for production scheduling using a combined genetic algorithm and multiagent model[J].Expert System，2020（38）：e12533.

[9]陈继文， 张译匀， 高晓明， 等. 基于改进遗传算法的PC构件生产调度优化[J]. 机械设计与制造工程， 2024， 53 （1）： 95-99.

[10]秦旋，朱倩影，韩家玄.预制构件生产-运输-装配一体化的建造调度优化[J].华侨大学学报（自然科学版），2023，44（3）：366-373.

[11]张瑞雪， 冯雪婷， 马贵仁. 基于NSGA-Ⅲ算法考虑碳排放的预制构件生产调度及运输优化[J]. 工程管理学报， 2023， 37 （2）： 153-158.

[12]熊福力，李琳琳.考虑生产与运输成本的准时制分布式预制构件生产调度[EB/OL].（2023-12-13）[2024-02-10].https：//doi.org/10.13196/j.cims. 2023. 0585.

[13]汪和平，齐欣然，陈梦凯. 基于NSGA-Ⅲ的装配式预制构件流水车间混合生产优化研究[J].管理工程学报， 2022， 36（1）： 240-251.

收稿日期：2024-05-20

作者简介：

杨荣正（通信作者）（1998—），男，工程师，机器学习、深度学习。

徐双双（1989—），男，工程师，机器学习、深度学习。

肖垚（1996—），男，工程师，机器学习、深度学习。

何新军（1996—），男，工程师，路桥施工。

王朝晨（1990—），男，工程师，路桥施工。