感悟基本思想，积累学习经验

2024-10-21朱月红

初中生世界·八年级 2024年10期

几何的魅力之一在于图形的对称之美。“夫美也者，上下、内外、小大、远近皆无害焉，故曰美。”《国语》中的这句名言，所强调的就是对称美。“轴对称图形”是“全等三角形”“轴对称”（小学所学）的发展和延续，也是后续进一步研究中心对称的基础。

整体感悟，形成知识结构

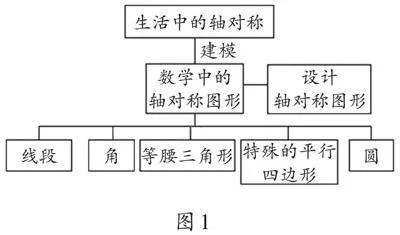
本章的内容包括轴对称与轴对称图形，轴对称的性质，设计轴对称图案，线段、角的轴对称性以及等腰三角形的轴对称性，运用性质作图等。通过对本章知识之间的逻辑关系进行归纳，我们可以得到一幅条理清晰、重点突出、关系严谨的思维导图（如图1）。

同学们，本章学习的基本过程是：概念及其基本性质→特例及其基本性质→数学内部的应用→在现实中的应用（欣赏、设计）。数学知识之间存在着一定的逻辑关系，这种关系体现了知识从哪里来、怎样形成、到哪里去。我们只有明确了知识的来龙去脉，方能从整体上真正理解数学知识。

“轴对称”的核心概念

当一个平面图形沿着直线l折叠后，如果直线l两边的图形能够互相重合，那么这个图形就叫作轴对称图形，而这条直线则被称为对称轴，直线l两边相互叠合的点是对应点，也叫对称点。值得注意的是，对称轴、对应点是两个关键词，由此可以派生出一系列对应几何元素，如对应线段、对应角、对应图形等。这些元素有助于我们探究轴对称图形的性质。

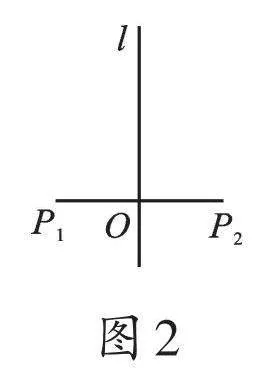
我们知道，确定轴对称变换的要素是对称轴。我们以此为“基准”，将对应元素与变换的要素联系起来，探究其中的不变量和不变关系，这就是研究轴对称基本性质的一般方法。在研究轴对称性质时，同学们要“有逻辑地思考”，可以按照“对应点→对应线段→对应角→对应图形”的层次展开对轴对称性质的研究。

例如，如图2，点P1、P2位于直线l的两侧，所以线段P1P2与直线l必相交，设交点为O。若平面沿直线l折叠后，点P1与点P2重合，则P1O与P2O重合，故P1O=P2O；这时，以O为顶点、l为邻边的两个邻补角也重合，所以直线l⊥P1P2，于是得到轴对称的基本性质：平面内，如果点P1和点P2关于直线l对称，那么线段P1P2被对称轴l垂直平分。

类比这样的探究方法，如果是两个图形关于直线l对称，它们又有怎样的关系呢？同学们可以结合图3，自主研究，并写下你的发现。

推理论证，提升能力

在应用知识的过程中，我们应注重数学规律的揭示，解题策略的优化，在本章利用图形探索和发现解决问题的方法。

例如图4，已知△ABC为等腰三角形。证明：等腰三角形底边上的高线、中线以及顶角平分线重合（三线合一）。

方法1：作AD平分∠BAC，则∠BAD=∠CAD。

在△ABD和△ACD中，

[AB=AC，∠BAD=∠CAD，AD=AD，]

∴△ABD≌△ACD（SAS）。

∴BD=CD，∠ADB=∠ADC=90°。

∴AD是△ABC底边上的高线、中线以及顶角平分线。

方法2：取BC中点D，连接AD。通过“SSS”可证△ABD≌△ACD，从而得到AD⊥BC，AD平分∠BAC。

方法3：作AD⊥BC，通过“HL”可证Rt△ABD≌Rt△ACD，从而得到AD平分∠BAC，BD=CD。