基于支持向量回归的数控加工刀轨自动规划方法

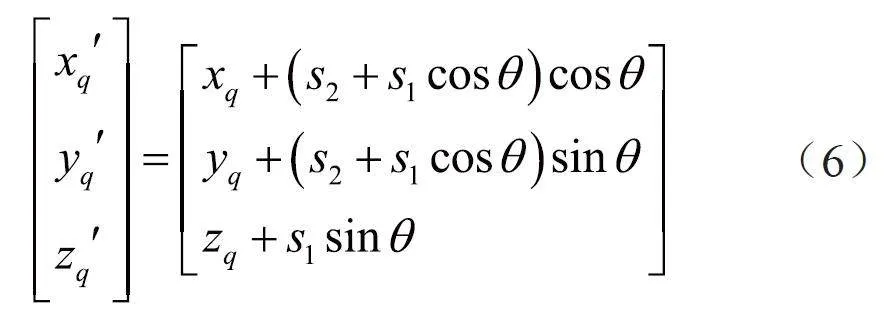
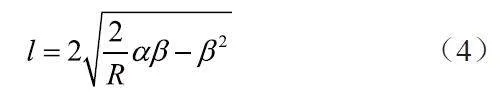
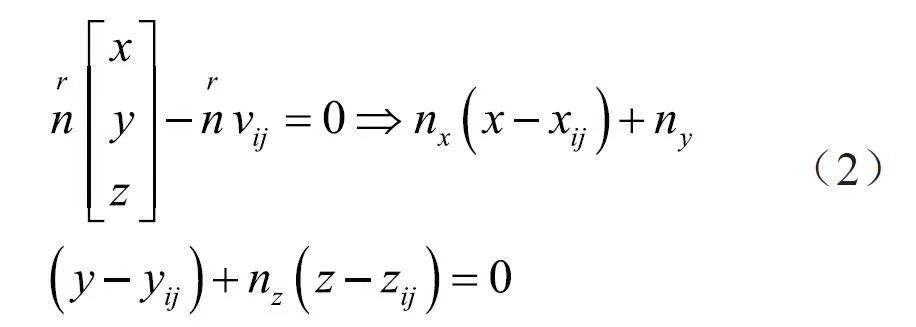
［摘 要］传统的刀轨规划方法基于经验公式和手工计算，效率低下且难以保证加工精度，对此文章提出基于支持向量回归的数控加工刀轨自动规划方法。试验结果表明，基于支持向量回归的数控加工刀轨自动规划方法可提高效率与加工精度，具有较高的实用价值。

［关键词］刀轨自动规划；数控加工；路径规划；支持向量回归

［中图分类号］D26.4 ［文献标志码］A ［文章编号］2095–6487（2024）04–0146–03

1 基于支持向量回归的数控加工刀轨自动规划方法的设计

1.1 提取数控加工刀具特征

在基于支持向量回归（SVR）的数控加工刀轨自动规划方法中，提取刀具特征是关键。这些特征需要根据加工任务、刀具类型和条件选择，可能还需进行降维处理。提取的特征应与刀轨数据相对应，以便训练SVR 模型来建立特征与刀轨参数之间的映射关系。

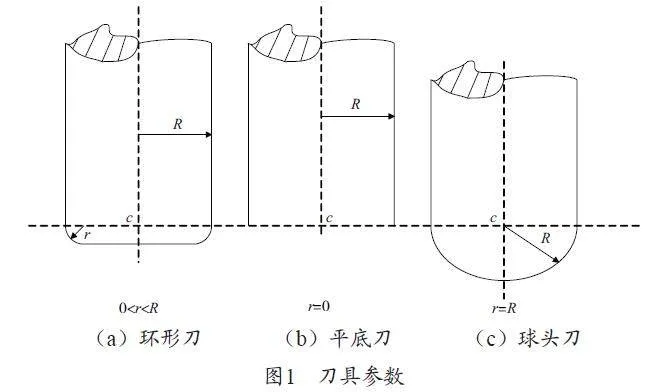
在数控加工中，经常使用的刀具包括平底刀、环形刀、球头刀3 种类型。刀具参数如图1 所示，其中环形刀的半径为R，球头刀与平底刀是环形刀的异形，当r=0 时为平底刀，当r=R 时为球头刀。

计算数控加工代码时，需考虑刀具类型和半径对轨迹的影响。球头刀因球心轨迹沿法矢方向偏移R 的特性，展现出良好的适应性和加工精度，且轨迹计算简便。所以文章选择球头刀进行规划分析，选取待加工的曲面s 等距刀轨半径之间的距离得出一个刀位面s'，其映射计算公式如下：

式中，Q为刀具轨迹所在超平面。

在刀位面上自动规划刀具轨迹，可避免刀具间的相互干扰。刀位点即球头铣刀的球心，位于被加工表面s 的刀位表面上。求解刀轨前需确定被加工面的刀面，并建立刀位面。基本思路为：将曲面上的三角形网格划分为单元，沿面法矢方向求出等距刀轨半径。

设定一三角面片Fi，其3 个顶点为vi=（vi0，vi1，vi2），顶点坐标为vij=（xij，yij，zij）（=0，1，2），该三角面片所在平面的表达式如式（2）所示：

刀具半径为R 时，则顶点vij 所对应的刀位点的表达式如式（3）所示：

vij'=vij+R'n（3）

在提取了刀位面、点等特征之后，刀轨自动规划方法可以利用这些特征来生成最优的刀具轨迹和切削参数，从而实现高效、精确的数控加工。

1.2 基于支持向量回归构建刀轨预测模型

SVR 是一种用于解决回归问题的监督学习算法，对噪声和异常值具有较好的鲁棒性。在数控编程中，刀具路径的生成与规划至关重要。为实现高效、精准的数控加工，需深入研究刀具路径的生成和规划。因此，研究选择SVR 进行数控加工刀轨自动规划设计。

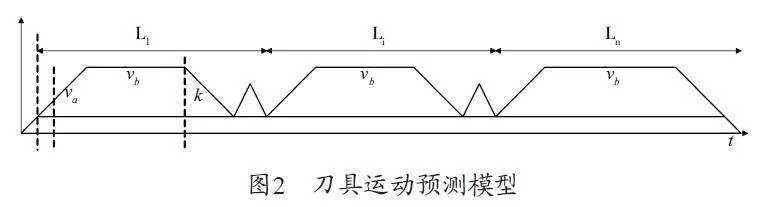
为了提升工作效率，刀具在规整的加工区域通常沿长度方向移动，如在狭长区域沿长轴移动，可显著减少移动时间。SVR 算法的关键在于寻找一个最优超平面，该平面并非直接拟合数据，而是根据数据分布特点反映整体趋势，然而，这一原理在复杂拓扑形状上难以应用。因此，针对数控加工领域，构建一种简化的刀轨预测模型。刀具运动预测模型如图2所示。

在刀具加速阶段va，数控加工能达到最大速度，加速度为k，在匀速切削状态中，走刀速度为vb。

刀具轨迹理论上由刀体与加工表面啮合关系确定，但受数控加工和表面表达方法的制约，通常以短直线段实现。走刀步长影响加工进度和效率：步长太大会降低精度，步长太小则会增加数据量，可能会引起速度波动，延长加工时间，影响效率和品质。因此，选择合适的步长是刀具轨迹规划的关键。

由于缺乏曲面局部区域的几何拓扑信息，在开始计算时难以确定一个满足精度要求的步长。因此，在没有足够的驱动点映射区域几何拓扑信息的情况下，可以先设定一个初始步长l，其数值应小于刀具的直径。满足数控加工精度要求的步长l 的计算公式如下：

式中，R为有效切削刃的刀具半径，α为加工局部区域的曲率半径，β为允许加工误差。

基于上述分析，文章设计的刀轨预测模型的表达式如下：

式中，D为切削间距，θ为刀具移行夹角。

当模型训练完成后，可以将其应用于实际的刀轨预测中。通过输入新的刀具信息、切削参数、工件材料信息等数据，模型可以预测出相应的刀具轨迹，为切削加工提供指导。

1.3 自动规划并生成刀轨路径

刀具路径规划算法的核心差异在于步长和行距计算方式。文章结合等残留高度与变步长策略，提出新的刀具路径规划方法。该方法是一个循环迭代过程，包括同条轨迹和相邻轨迹间刀位点数据的计算，可实现高效且精确的刀具路径规划。

文章设计的刀轨规划算法的具体步骤如下。

（1）确定刀具的起始路径位置，以最大的表面边界为第一条刀位点的轨迹。

（2）对原始轨迹进行离散，由上述步骤得到一组满足精度指标的刀位点。

（3）求出相应的刀位点，按行间距公式求出相应的刀位点。

（4）生成相近路径，将每个相应的刀位点连接起来，拟合出的刀位点用来延长或剪裁所需的刀位点，使得它们的端点位于该曲面的边界上，生成相邻的刀位点轨迹。

（5）重复步骤（2）、（3）、（4），直至完全涵盖数控加工处理区域。

（6）按照式（6），将刀位点转化为刀触点，然后按一定的次序进行联接，即完成刀轨路径的自动规划。对于刀位点vij'（xq，yq，zq）转换为刀触点的计算公式如下：

式中， s 1为原始轨迹路径长度， s 2为刀位点半径长度。

2 试验测试与分析

2.1 试验准备

为验证文章提出的基于支持向量回归的数控加工刀轨自动规划方法的有效性，本次测试以Matlab 软件为试验平台，试验参数选定见表1。

本次测试选择一曲面的一条边界线为刀具的初始路径，使用文章所提方法对刀轨中的刀位点进行规划，检验其与实际设定刀轨路径是否吻合。

2.2 试验结果与分析

基于上述试验准备，在Matlab 软件中建立了测试曲面，文章所提方法与实际的刀位点位置的测试结果见表2。

由表2 可知，基于支持向量回归的数控加工刀轨自动规划方法在试验中表现出了良好的规划性能。通过合理地选择模型参数和切削参数，可以实现对刀轨路径的准确预测，为数控加工过程提供有效的指导。然而，在实际应用中，还需要考虑更多的因素，如刀具磨损、材料特性等，以进一步提高刀轨规划的准确性和鲁棒性。

3 结束语

文章提出的基于支持向量回归的数控加工刀轨自动规划方法，利用机器学习技术实现智能、自动规划。SVR能够准确捕捉加工过程中的复杂非线性关系，生成更合理、高效的刀轨，提高加工质量、减少加工时间和能耗，并具有较好的泛化能力。然而，该方法仍面临参数优化和模型泛化等挑战。未来，将继续深入研究，不断优化和完善该方法，以期在数控加工领域实现更为广泛的应用。

参考文献

[1] 沈玉明，吴晓鸣，冯沛儒，等. 基于支持向量回归代理模型的STATCOM 协同规划方法[J]. 电工电能新技术，2023，42（10）：66-73.

[2] 吕玉，辜桂香，聂江勇. 面向五轴数控加工刀轴运动控制的平滑控制算法研究[J]. 自动化与仪器仪表，2023（12）：85-88.

[3] 陈波，叶玉全，王志标，等. 复杂槽轮零件数控加工工艺设计及仿真研究[J]. 内燃机与配件，2023（17）：103-105.

[4] 王天力，刘威，范吕阳，等. 自由曲面等误差数控加工刀轨生成方法[J]. 组合机床与自动化加工技术，2023（3）：13-16.