干扰观测器与模糊伺服复合控制策略研究

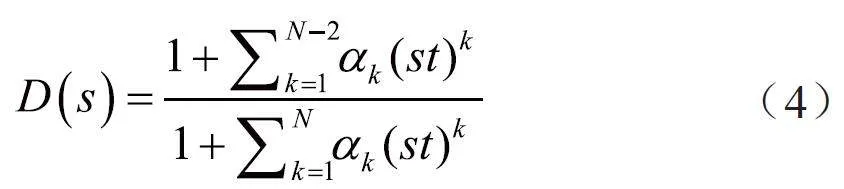
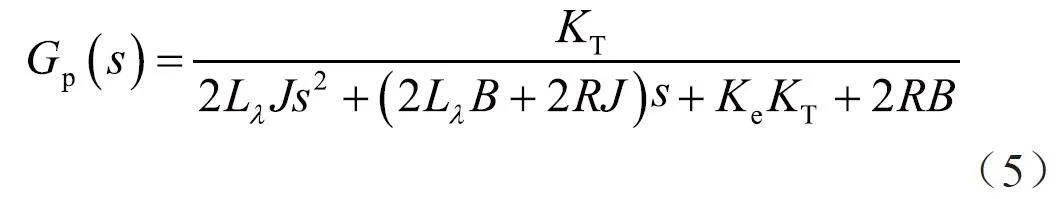
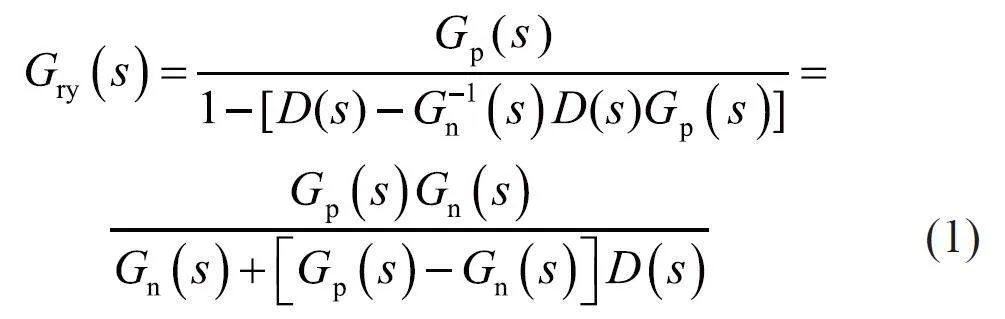
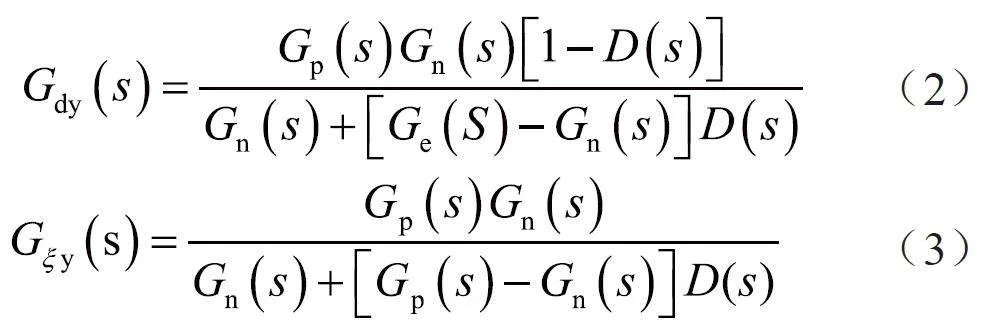
［摘 要］在现代工业伺服控制技术发展中，伺服控制系统的高控制精度、高稳定性和快速响应性是经典控制理论和现代控制原理追求的主要目标，特别是在外界对系统的扰动或难以建立精确的被控对象数学模型的情况下，传统的单纯PID 控制环路抗扰动能力差。文章设计了模糊控制器和干扰观测器，该控制器能够补偿模型参数不准确所引起的误差，同时能够抵抗外界对系统的扰动。

［关键词］PID 控制；干扰观测器；模糊控制；复合控制

［中图分类号］TM351 ［文献标志码］A ［文章编号］2095–6487（2024）04–0144–03

1 背景

在经典控制方法中，系统输出的稳定性和控制精度是主要追求目标，PID 控制因其简易理论基础，控制过程易于调节且控制效果突出，通过适当改变其控制环路结构，能够有效改善其输出效果，因此广泛应用于工业各控制领域。在实际工业应用中，因控制环境的多样性，且PID 控制自身的局限性，特别是对于控制对象的不确定性和一些非线性系统，单纯PID伺服控制环路已不能满足控制要求。模糊控制不仅不受限于被控对象精确的模型理论，还能够适应于一些控制域复杂的非线性系统，因此能够很好地填补PID控制的一些缺陷。

2 干扰观测器设计

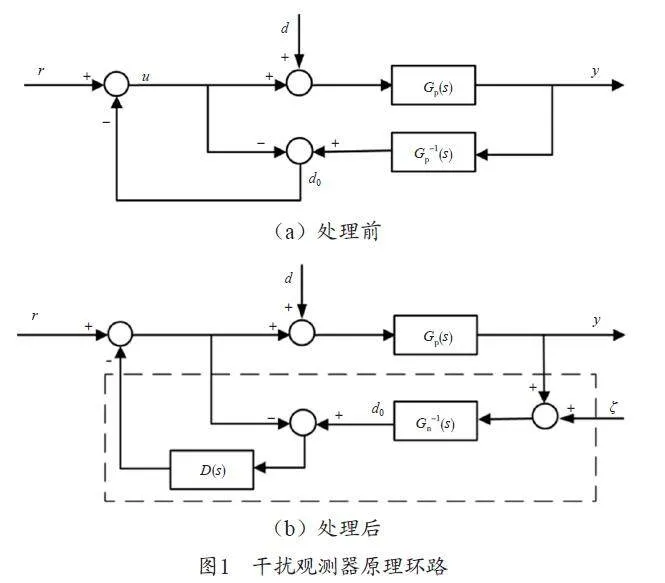
干扰观测器控制的基本思想是将外部各种干扰因素及模型参数变化引起的实际对象与名义模型输出的差异等效到控制输入端，即观测出等效干扰，在控制系统中引入相等的补偿量实现对干扰的完全抑制。干扰观测器原理环路如图1 所示。

由图1（a）可知，等效干扰估计值为：do=（u+d）Gp（s）Gp-1（s）–u=d，其中u 为输入信号减去反馈信号，d 为外界干扰，Gp（s）为被控对象传递函数，do 为干扰估算值，由此可看出，外界对系统的干扰是可以估算的。

在实际控制系统中，被控对象的传递函数为正则，分析图1 可发现，在环路图中引入了被控对象传递函数的逆函数，可通过在图1（a）中引入一个低通滤波器来满足，同时考虑引入测量噪声的影响，经过处理后的原理如图1（b）所示，图中虚线框内为干扰观测器，其中ξ、Gn-1（s）和D（s）分别为测量噪声、名义模型的逆和低通滤波器。

利用梅逊公式可求得图1 中输入信号r、干扰d、测量噪声ξ 对系统输出y 的传递函数：

式中，N与系统阶次成正比，k为传递函数阶次，t为时间。

同理：

对D（s）的设计准则通常采用的是在低频段D（s）=1 和在高频段D（s）=0，由此对上述公式进行分析可得：在低频段Gry（s）=Gn（s），Gdy（s）=0 和Gξy（s）=1，在高频段Gry（s）=Gp（s），Gdy（s）=Gp（s）及Gξy（s）=0。由此分析可知，在低频段时实际被控对象对系统输入时响应的传递函数与名义模型一致，Gdy（s）=0 说明低通滤波器能够完全抑制低频干扰，Gξy（s）=1 说明在低频段测量噪声ξ 对干扰观测器的影响非常大。

对于低通滤波器的设计可采用以下公式：

3 模糊控制器构建

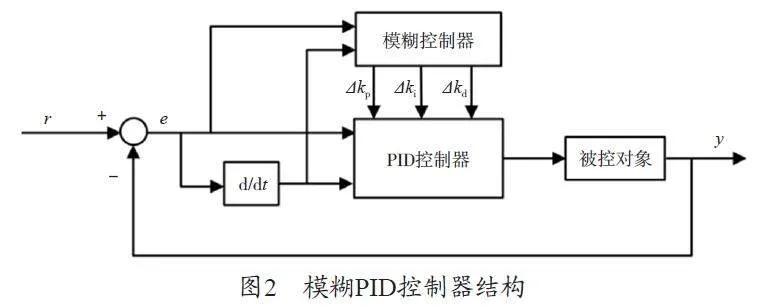
模糊PID 复合控制策略：模糊控制能够适应非线性特性控制对象，且鲁棒性好，控制精度主要由模糊规则库决定，由于没有积分（I）的作用，在实际的伺服控制应用中不能消除静态误差，而模糊PID 复合控制能够充分发挥各自控制优势。模糊PID 控制器结构如图2 所示。

若x 的物理论域为[X，–X]，模糊论域为[F，–F]，则量化因子kf=F/X，同时需要保证经过量化因子处理后的变量值在模糊论域范围内，若被控对象需要输入的物理论域为[P，–P]，则比例因子kx=P/X。模糊规则库可利用MATLAB/Simulink 工具建立，如在实际控制应用中，当|e| 较大时，为了能够增加系统响应速度，同时为了提高系统动态稳定性，kp 应取较大值，且kd 应取较小值，同理对于变量e 或ec，其他输入情况同样能够建立这种输入变量与输出变量间的对应关系。

4 观测器PID控制试验

假设被控对象为1 个伺服电机，其传递函数为线电压U 与转子角速度w（t）输入输出的关系w（s）/U（s），即无刷直流电机传递函数Gp（s）为：

式中，Ke为反电动势系数，R为定子绕组的电阻值，J为电机转子转动惯量，B为粘性阻尼系数，KT为转矩常数，L为三相定子绕组自感，M为定子绕组间互感（L–M=Lλ）。

令K1=2LλJ，K2=2LλB+2RJ，K3=KeKT+2RB，可得：

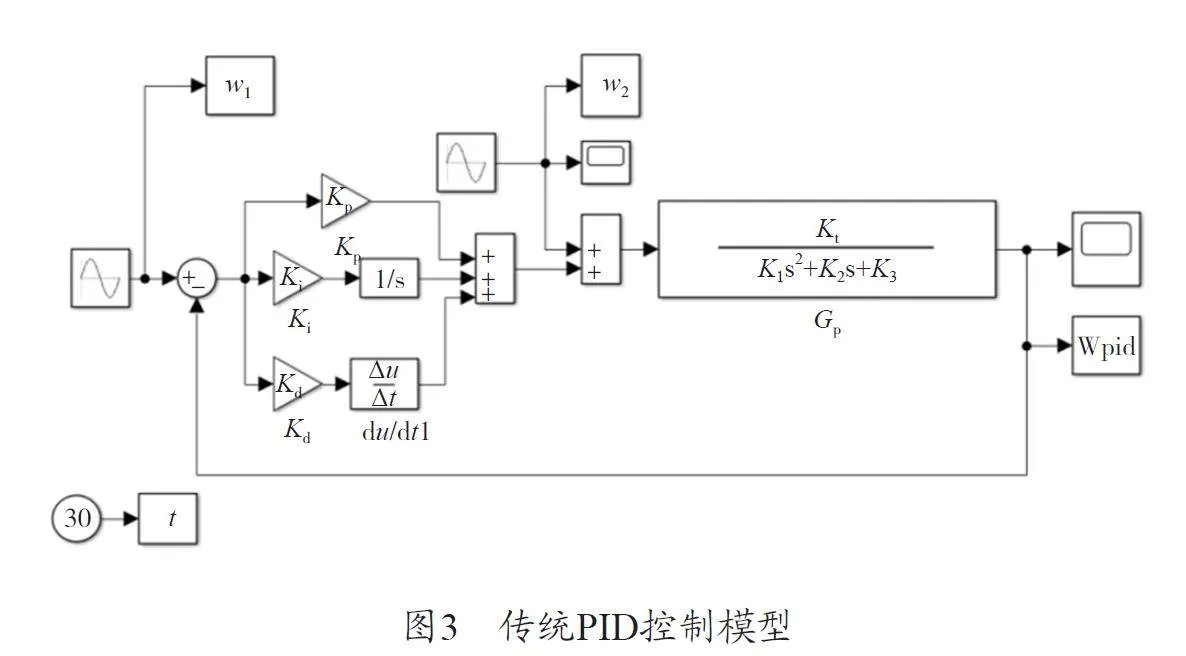
通过MATLAB/Simulink 建立的传统PID 控制模型如图3 所示。

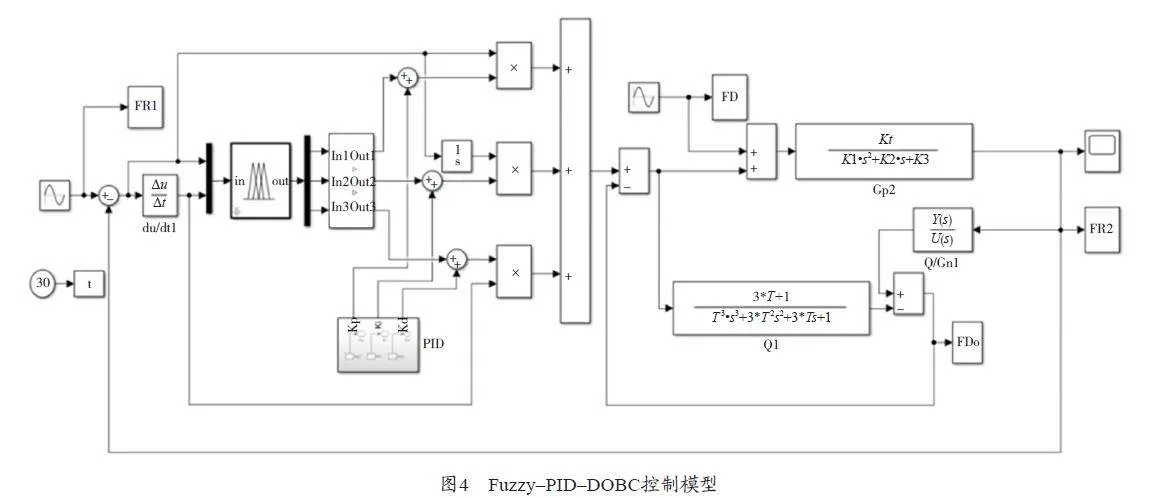
建立基于观测器控制的模糊PID 控制（Fuzzy–PID–DOBC）模型，如图4 所示，系统输入信号及信号变化率输入到模糊控制器，模糊控制器输出作为PID控制环路的输入，与PID 控制综合实现控制参数的在线整定，能够减少系统调节时间，还能够提高系统的鲁棒性。DOBC 处于内环，其输入为模糊PID 复合控制的输出。根据Fuzzy–PID–DOBC 控制输出结果，其误差范围在–0.013～0.012。

5 结束语

文章根据模糊控制基本思想构建了模糊控制器，在完成干扰观测器设计和模糊控制器构建的基础上，利用MATLB/Simulink 建立了基于干扰观测器控制的模糊PID 复合控制策略模型并完成了试验。研究结果表明，引入干扰观测器之后对系统扰动有明显的抑制作用，控制精度明显提高。同时为了系统能够实现控制参数在线整定、提高系统响应速度和增加系统鲁棒性，引入了模糊控制，根据输出结果可知，显著改善了系统性能。

参考文献

[1] 刘金琨. 先进PID 控制MATLAB 仿真：第3 版[M]. 北京：电子工业出版社，2011.

[2] 刘经伟，周瑞，朱敏玲. 先进模糊智能复合经典PID 控制理论与应用及其MATLAB 实现[M]. 北京：首都经济贸易大学出版社，2016.

[3] 李国勇，杨丽娟. 神经· 模糊· 预测控制及其MATLAB实现：第3 版[M]. 北京：电子工业出版社，2013.