一题三类通

二面角是从一条直线出发的两个半平面所组成的图形。有关二面角大小的考查是当前新高考的重点也是难点，其综合性较强、方法灵活，它能有效地培养同学们的空间想象、逻辑推理、运算求解等能力。下面以2024年新高考全国Ⅰ 卷第17 题为例，引入三类通法，详细叙述具体步骤，希望对同学们解题的探索性、灵活性、独创性带来启示。

注：凡二面角问题中含有可求原图形面积和该图形在另一个半平面上射影图形面积的，都可利用射影面积公式求出二面角的大小，具体数量关系复杂的时候可以引入三角函数来简化计算过程。

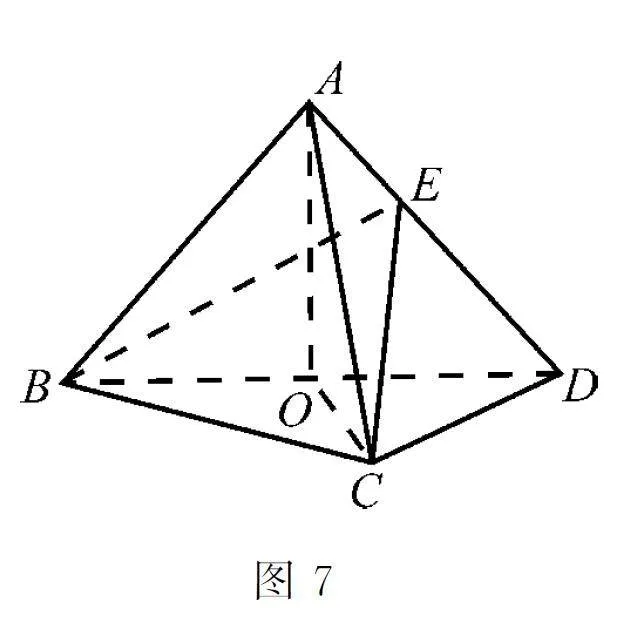
巩固练习：（2021年新高考全国Ⅰ卷第20题）如图7，在三棱锥ABCD中，平面ABD ⊥平面BCD，AB=AD，O为BD 的中点。

（1）证明：OA⊥CD;

（2）若△OCD 是边长为1的等边三角形，点E 在棱AD 上，DE=2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD 的体积。

提示：（1）略。

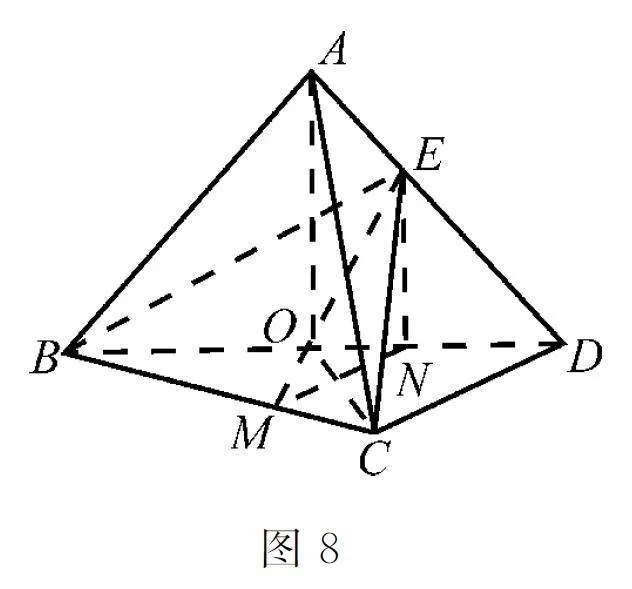
（2）如图8所示，过点E 作EN ∥AO 交BD 于N ，过点N 作NM ∥CD 交BC 于M ，连接ME，则可得EN ⊥平面BCD 。

由OB=OD =OC可得，△BCD 为直角三角形。从而可得∠EMN 为所求的二面角E-BC-D 的平面角，即∠EMN =45°，可得MN =EN 。再结合平行关系和△OCD 是边长为1的等边三角形，可求出三棱锥的体积。

总结：高中数学重点在培养同学们的思维能力、数学核心素养，这是高考评价体系中所述的“多停下来想一想，多些思考，少些计算”的鲜明要求，也是新高考试题的明显导向。而一题多解能激发同学们自主思考，并逐步提升分析问题、解决问题的能力，进而提升创新思维，最终促进创新能力的发展。

（责任编辑 赵 倩）