基于Transformer的旅行商问题解法

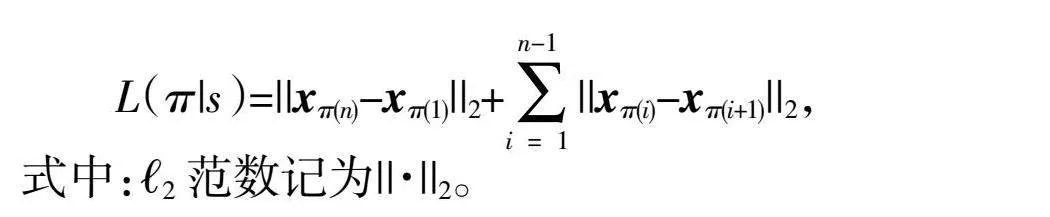
摘 要：在针对旅行商问题（Travelling Salesman Problem）的近似求解算法中，传统启发式算法收敛速度较慢，准确性较低。为解决上述问题，该文提出一种基于Transformer的神经网络方法。该方法使用神经网络，可有效提高近似解的求解速度和准确性，并使用Transformer注意力机制全面提高神经网络的性能。该方法使用强化学习进行训练，使用束搜索算法进行搜索。使用该方法对随机50节点的旅行商问题进行测试，试验结果表明该种基于Transformer的旅行商问题解法，可在较低的复杂度前提下，得到近似于精确解的效果。

关键词：旅行商问题；Transformer；注意力机制；神经网络；近似求解

中图分类号：TP18 文献标志码：A 文章编号：2095-2945（2024）29-0161-05

Abstract： In approximate solutions to the traveling salesman problem （TSP）， traditional heuristic algorithms are known for their slow convergence speed and low accuracy. To address these issues， this paper proposes a neural network approach based on Transformers. This method utilizes neural networks to effectively improve the speed and accuracy of approximate solutions， while leveraging the Transformer's attention mechanism to enhance the overall performance of the neural network. This method uses reinforcement learning for training and beam search algorithm for search. This method is used to test the random 50-node traveling salesman problem， and the experimental results show that the solution of the traveling salesman problem based on Transformer can get the effect which is similar to the exact solution under the premise of low complexity.

Keywords： traveling salesman problem; Transformer; attention mechanism; neural network; approximate solution

旅行商问题（Travelling Salesman Problem，简称TSP）是组合优化问题中一类经典的NP完备问题，具有较高搜索空间和复杂度。它的理论全搜索复杂度为O（n！）。旅行商问题可以被描述为在给定n个城市以及各个城市间距离的条件下，有一个旅行商需要从一个城市开始，逐一访问每个城市，每个城市仅访问一次，并在访问完所有城市后返回出发城市。问题在于如何规划路径，以使旅行商所走的总路径最短。其数学模型：对于城市V={v1，v2，…，vn}的一个访问顺序为T=（t1，t2，…，tn），其中ti∈V（i=1～n），且tn+1=t1， 则问题为求min，其中为这n个城市不重复排列的所有可能的回路。

旅行商问题求解方法及其相关方法具有广泛的工业应用场景，例如路径规划、生产规划、供应链和计算机网络等领域。因此，该问题引起了多学科研究者的关注，并驱动了一系列重要的优化方法的发展，包括切平面法、分支定界法、局部搜索算法、拉格朗日松弛法和模拟退火算法。

1 研究现状分析

当前，旅行商问题求解方法主要分为精确求解方法与近似求解方法。精确求解方法可确保得到最优解，但当问题规模增大时，计算成本显著增大。而近似求解方法牺牲最优性，换取部分计算效率，可在允许的时间内得到较优解。

1.1 传统方法

1.1.1 精确求解方法

旅行商问题的精确求解方法有穷举法、动态规划和整数规划算法。Held和Karp[1]提出了一种可用于求解旅行商问题的动态规划算法，复杂度为O（n22n），这种算法在n>40时就难以求解。Gu等[2]给出了一种备有切平面法和分支定界法的通用整数规划求解器。最后，Cook等[3]设计了一种高度专业化的旅行商问题精确求解方法，称为Concorde，被广泛认为是目前对于大规模旅行商问题最快的精确求解方法。

1.1.2 近似求解方法

旅行商问题的近似求解方法主要为元启发式算法，例如最邻近搜索算法、遗传算法、模拟退火算法、禁忌搜索算法、蚁群算法和树木生理算法等。Halim等[4]通过计算时间、统计数值、收敛性3个维度，对比了以上6种主要的元启发式算法。于计算时间维度而言，最佳算法为最邻近搜索算法，其次为树木生理算法和遗传算法。于统计数值维度而言，最接近最佳路径的算法有禁忌搜索算法、树木生理算法、遗传算法。于收敛性维度而言，最邻近搜索算法、禁忌搜索算法、蚁群算法表现较优。

由于以上元启发式算法各有优劣，一些研究者曾尝试使用多种元启发式算法进行改进与融合，例如Lee[5]成功地将遗传算法与蚁群算法进行结合与优化，同时保有了遗传算法与蚁群算法的优势，并取得更佳的效果。其中，具有代表性的是Google OR-Tools[6]，其为一个高度优化的程序，可用于解决旅行商问题和更大规模的车辆路径规划问题。该程序采用了不同的元启发式算法，如模拟退火算法、贪婪下降算法、禁忌搜索算法，在搜索空间中进行搜索，并通过局部搜索技术得出较优解。目前，求解旅行商问题最佳的元启发式算法为LKH-3算法，作为Lin-Kernighan-Helsgaun TSP求解器的衍生版本。

1.2 神经网络方法

神经网络方法是一种机器学习方法，其通过模仿生物神经网络的结构和功能，在计算机视觉、自然语言处理、语音识别等领域有广泛的应用。近年来，为求解旅行商问题，许多使用神经网络方法的新型近似求解方法开始出现。相对于传统方法，这种新型近似求解方法，可有效提高近似解的准确性。这为求解组合优化问题的发展指明了新的方向。使用神经网络方法求解旅行商问题的典型算法包括Hopfield神经网络、指针网络、强化学习指针网络等。

随着神经网络方法的日益发展，一种类似于人的大脑中注意力机制的神经网络——注意力网络应运而生。这种网络最早出现在计算机视觉领域，后来被广泛应用于自然语言处理领域。2017年，Google团队最具代表性地在“Attention is all you need”一文中提出Transformer模型结构和注意力机制，由此注意力机制成为研究热点。注意力机制全面提高了神经网络模型的性能，大力推动了神经网络方法的发展，是机器学习领域的一次历史性变革。

2 Transformer基本框架及组成

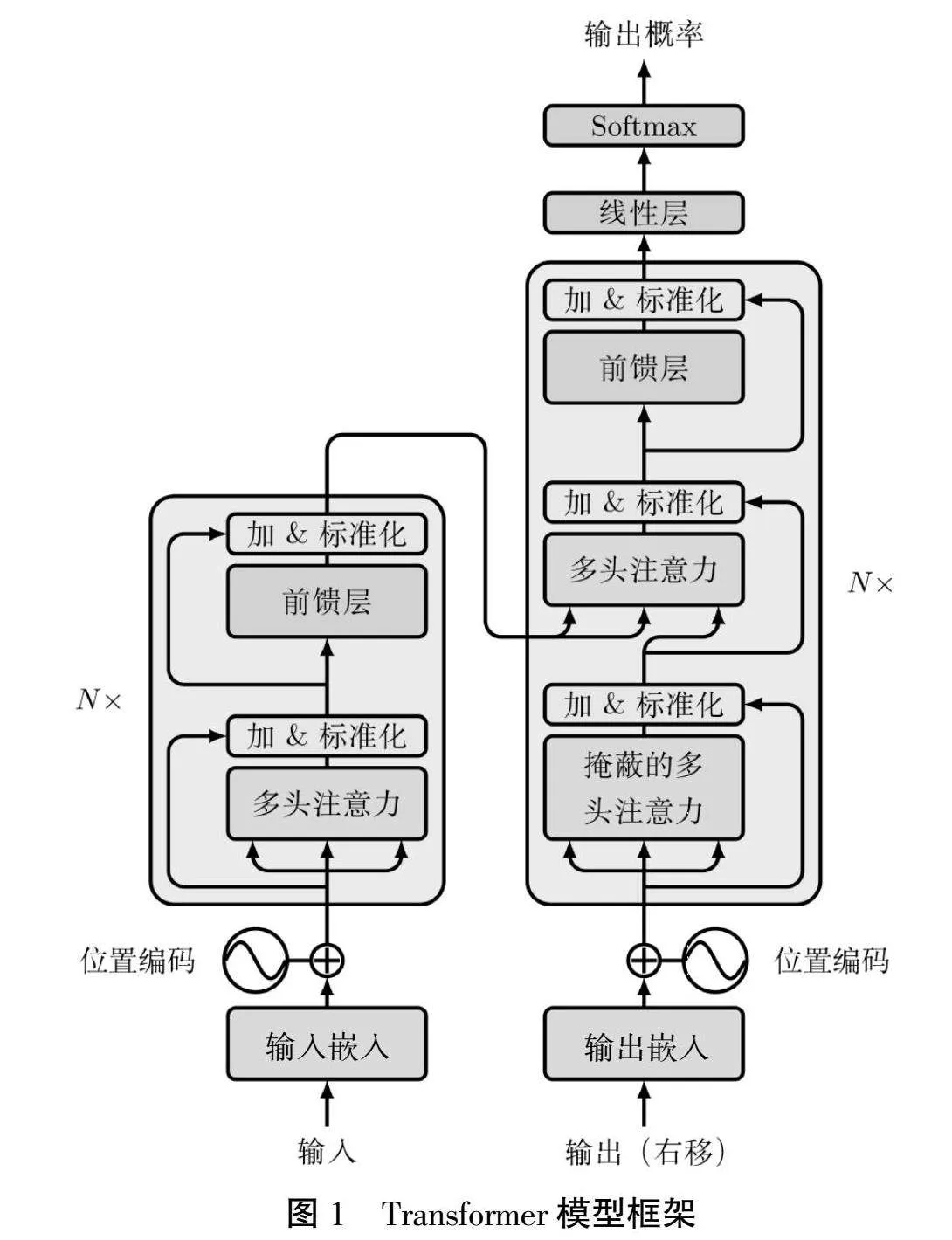
Transformer的基本框架由编码器和解码器构成，如图1所示[7]。编码器将一个由符号表示组成的输入序列（x1，…，xn）转化为连续性表示形式z=（z1，…，zn）。在给定z的情况下，解码器能逐元素地构造输出序列，表示为（y1，…，ym）。在每一步中，模型均为自回归性质，将之前生成的符号作为附加输入，供下一步的生成使用。

编码器由N=6个相同的层级构建而成。各层级分为2个子级。首个子级为一个多头自注意力机制层，随后的子级则为一个基础的位置全连接前馈网络。在每个子级上，实施残差连接及层标准化。

解码器同样由N=6个相同的层级构建而成。相较于在编码器中的2个子级，解码器中增添了第三个子级，其主要功能是对编码器的输出进行多头注意力机制层的处理。在每个子级上，同样实施残差连接和层标准化。此外，为了阻止对后续位置的关注，解码器对堆栈中的自注意力子级进行了修正。这种遮蔽操作配合了对输出嵌入位置的偏移，保证了位于i的预测仅依赖于小于i的已有输出。

3 基于Transformer的旅行商问题解法框架

给定一个输入图，表示为二维空间中的n个城市：s={xi}，其中每个xi∈ 2。路径定义为所有点的置换？仔。优化目标是使路径的长度最短，其中路径的长度定义为

L（|s）=||x（n）-x（1）||2+||x（i）-x？仔（i+1）||2，

式中：2范数记为||·||2。

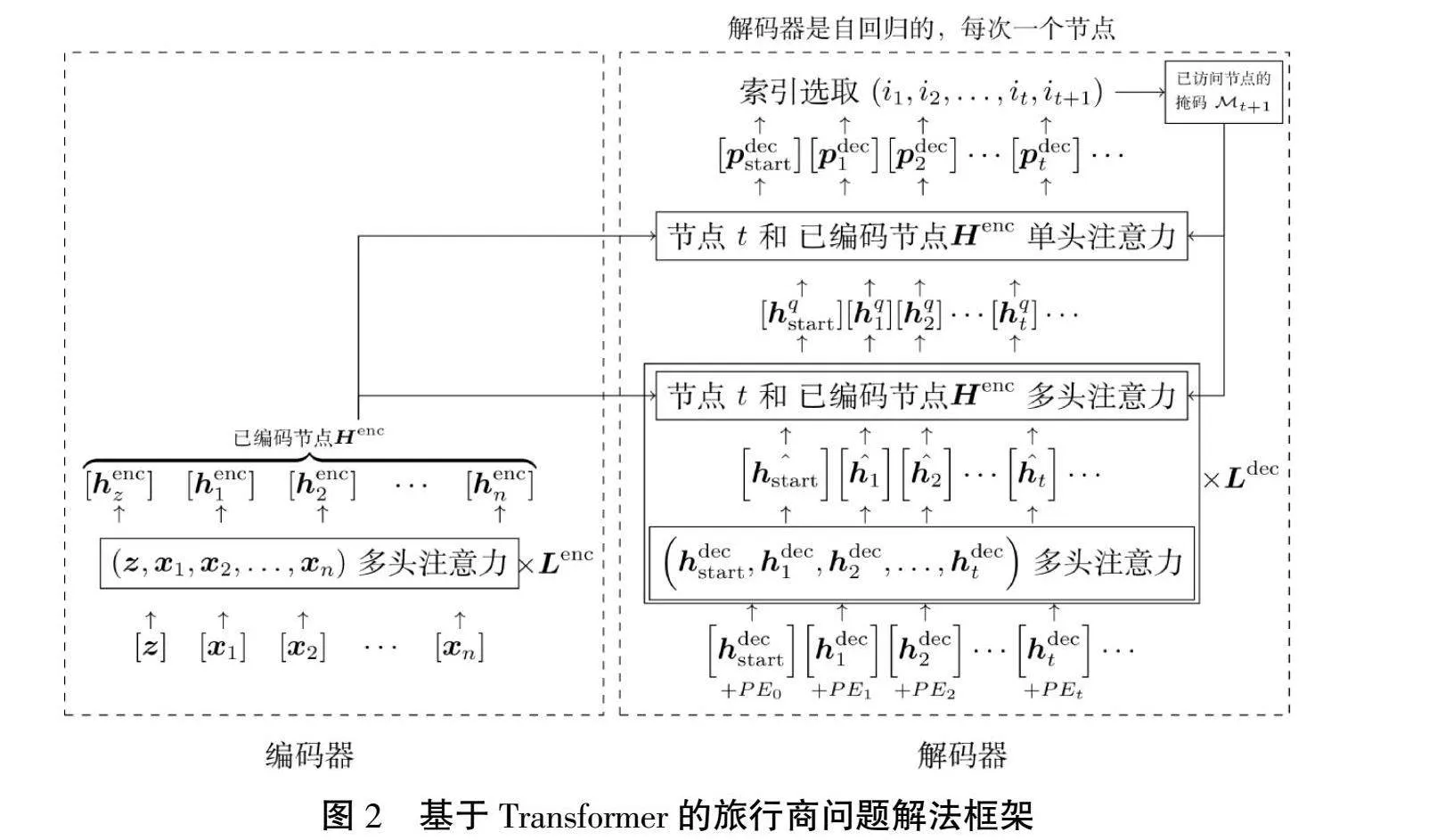
旅行商问题可视为序列到序列的“翻译”类问题。其中，“源语言”为二维平面上的点集，“目标语言”是最短长度的路径，设计类Transformer模型可解此问题。基于Transformer的旅行商问题解法框架如图2所示。

3.1 编码器

编码器是一个标准的Transformer编码器，有着相同的多头注意力机制层和残差连接。Kool等[8]指出，批标准化在路径规划问题中，较层标准化有更优效果，此处将层标准化改用为批标准化。其数学表达式（仅考虑单头注意力机制层以简化描述）为

Henc=H∈ （n+1）×d，

其中，H=0=Concat（z，X）∈ （n+1）×2，z∈ 2，X∈ n×2，

H+1＝softmax∈ （n+1）×d，

Q=HW∈ （n+1）×d，W∈ d×d，

K=HW∈ （n+1）×d，W∈ d×d，

V=HW∈ （n+1）×d，W∈ d×d，

z为随机生成的起始点。

3.2 解码器

解码器是自回归的，每次一个城市。假设已确定路径中的前t个城市，以预测下一个城市。模型使用链式分解将路径概率分解为

p（|s）=p（（i）|（<i），s）。

3.2.1 解码器的第一部分

解码器的第一部分是位置编码。对于已选的城市it为

式中： 为位置编码，则

PEt，i=sin（2？仔fit） 如果i为偶数，cos（2？仔fit） 如果i为奇数，那么fi=。

3.2.2 解码器的第二部分

解码器的第二部分是对已知路径的嵌入。此注意力机制层是标准的，使用多头注意力机制，残差连接和层标准化。其数学表达（仅考虑单头注意力机制层以简化描述）为

3.2.3 解码器的第三部分

解码器的第三部分在未访问的城市中，对下一个可能的城市进行查询。此处应用了多头注意力机制，残差连接和层标准化。其数学表达（仅考虑单头注意力机制层以简化描述）为

式中： 为已访问城市的掩码； 为哈达玛积。

3.2.4 解码器的第四部分

解码器的第四部分使用单头注意力机制对未访问的城市进行最终查询，以得到概率分布。其数学表达为

式中：C=10。

3.3 模型训练

使用强化学习对模型进行训练。给定模型？兹和s，损失函数定义为

J（|s）=E～p（.|S）L（|s）。

定义图分布S，训练期间图从中采样。整体训练目标定义为

J（）=Es～S[J（|s）]。

通过梯度下降方法最小化损失函数。给定基线b（s），可使用Williams[9]的REINFORCE梯度估计算法为

J（|s）=E～p（.|s）[（L（|s）-b（s））logp（|s）]。

通过Monte Carlo采样方法，梯度可估计为

J（）（L（k|sk）-b（sk））log（p（k|sk））。

3.4 搜索策略

在搜索策略中，可找到最优解的穷举方法的复杂度为O（n！），难以求解。因此，搜索策略的估计是必要的。最简单的搜索策略估计是贪婪搜索，即在每一个时间点，总选取最高概率的下一个城市为？仔（i）=argp（j|（<i），s）。在此基础上的另一搜索算法为束搜索算法，与贪婪搜索相比，束搜索在每一步都会保存当前最佳的B个候选序列，以提高搜索准确性。为有效提高搜索准确性，本文采用束搜索算法进行搜索。

4 算法测试

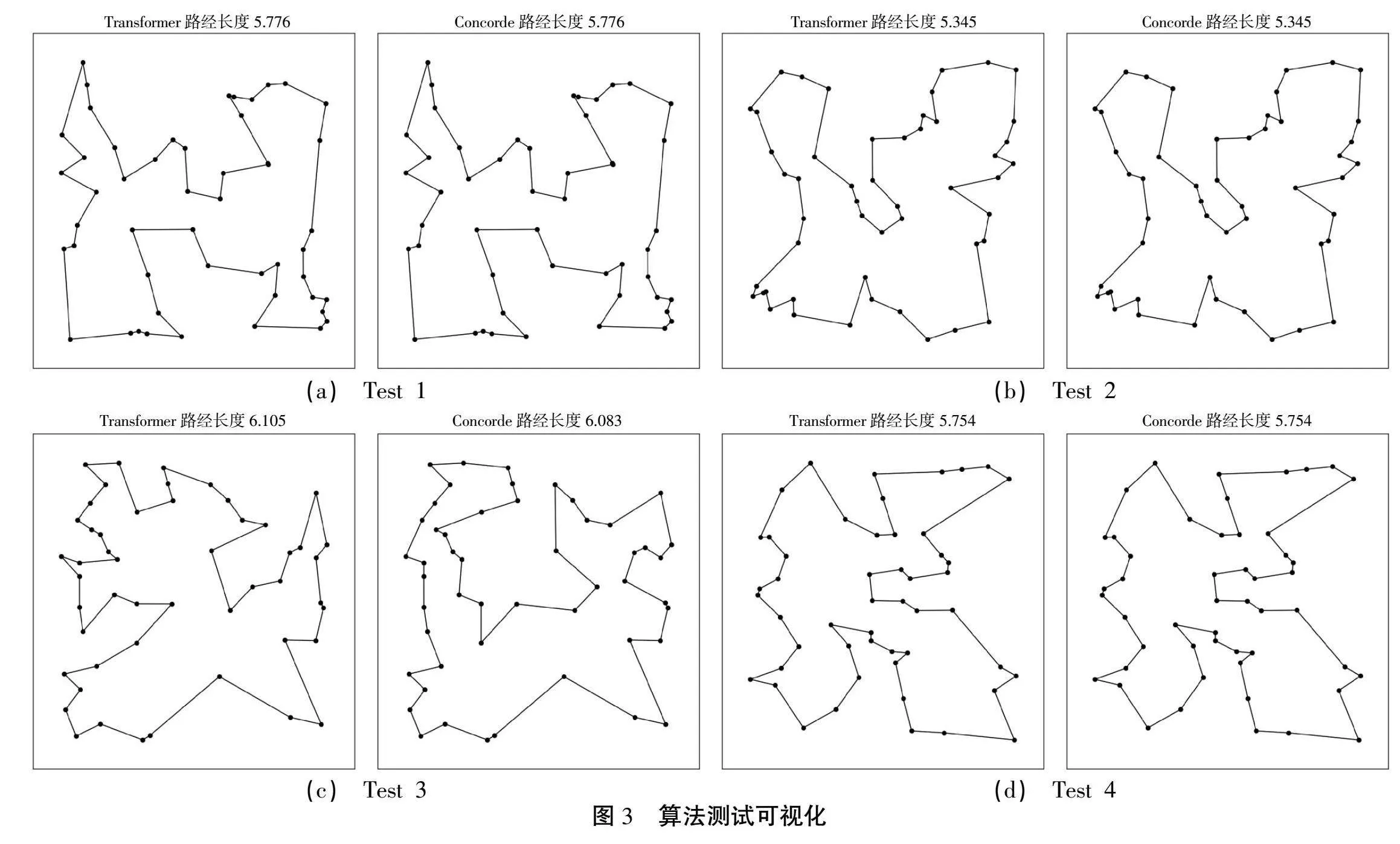
随机选用50节点的旅行商问题，对上述解法进行测试。由于Concorde算法可得旅行商问题的精确解，文中采用其结果进行可视化对比分析（图3）。

可视化图像分别呈现的是4次试验结果。在第i次试验Test i中，左子图为基于Transformer的旅行商问题算法结果的可视化，右子图为Concorde算法结果的可视化。其得出的路径长度分别标注于子图上方。从图3中可以看出，在第一、第二、第四次试验中，基于Transformer的旅行商问题算法得出了与Concorde算法相同的解。在第三次试验中，Transformer的路径长度为6.105个单位长度，Concorde的路径长度为6.083个单位长度。结果分析表明，基于Transformer的旅行商问题解法可较好地得出较优解，其结果与Concorde精确解近似。

5 结论

基于Transformer的旅行商问题解法，可在较低的复杂度前提下，得到近似于精确解的效果。Transformer在组合优化领域中具有巨大的应用潜力。传统精确解法，如Concorde等算法，在求解精确解的应用场景中仍然具有优势。随着Transformer在此应用场景研究的深入，后续研究可能将聚焦于超大规模旅行商问题解法的研究中。由于GPU内存限制及Transformer复杂度仍有O（n2）L，使用Transformer方法求解大型旅行商问题仍具挑战性。

参考文献：

[1] HELD M， KARP R M. A dynamic programming approach to sequencing problems [J]. Journal of the Society for Industrial and Applied mathematics， 1962，10（1）：196-210.

[2] GU Z， ROTHBERG E， BIXBY R. Gurobi [Z]. 2008

[3] COOK W J， APPLEGATE D L， BIXBY R E， et al. The traveling salesman problem： a computational study [M]. Princeton university press， 2011.

[4] HALIM A H， ISMAIL I. Combinatorial optimization： comparison of heuristic algorithms in travelling salesman problem [J]. Archives of Computational Methods in Engineering， 2019，26：367-380.

[5] LEE Z J. A hybrid algorithm applied to travelling salesman problem[C]//proceedings of the IEEE International Conference on Networking， Sensing and Control， 2004，F，2004.

[6] FURNON V， PERRON L. OR-Tools Routing Library [Z].

[7] VASWANI A， SHAZEER N， PARMAR N， et al. Attention is all you need[C]//Advances in Neural Information Processing Systems，2017：5998-6008.

[8] KOOL W， VAN HOOF H， WELLING M. Attention， learn to solve routing problems！[R]. arXiv preprint arXiv：180308475，2018.

[9] WILLIAMS R J. Simple statistical gradient-following algorithms for connectionist reinforcement learning [J]. Machine learning， 1992，8：229-56.