新课标背景下初中数学解题技巧的教学策略探究

【摘要】随着新课程标准的施行，初中数学愈发关注学生数学解题关键能力，利用有效策略向初中生传授数学解题技巧已然成为教师教学的关键任务.在这样的背景下，文章分别从选择、填空题以及解答题这三大题目类型出发，结合排除法、特殊化法、整体代入法、逆向思维、数形结合、待定系数法、分类讨论思想等解题技巧，探讨新课标背景下初中数学解题技巧的教学方法，旨在提高解题教学质量，促进学生素养发展.

【关键词】新课标；初中数学；解题技巧；教学策略

《义务教育数学课程标准（2022年版）》（以下简称《新课标》）指出义务教育阶段的数学教学应使人人都能获得良好的数学教育，不同的人在数学上得到不同的发展.此背景下在组织初中数学解题教学期间，教师需要关注技巧的渗透，把握《新课标》的教学要求，同时结合学生的思维能力合理安排教学活动，从根本上帮助学生掌握不同类型题目的解题方法，快、准、稳解决问题，落实核心素养.

一、选择、填空题解题指导

要充分利用题干和选择题两方面提供的信息，依据题目的具体特点，灵活、巧妙、快速地选择解法，以便快速智取，这是解选择题与填空题的基本策略.在教学期间，教师需要渗透“小题小做，小题巧做，切忌小题大做”的基本原则，采用以下三种较为便捷的方式开展解题教学，引导学生做到运算要快、变形要稳、答案要全、解题要活、审题要细，避免在选择以及填空题中失分.

（一）排除法解决问题

排除法是解决选择题常规的一种解决方法.在解决此类问题期间，教师要引导学生做到“一看、二抓、三领、四想”，先看设问，弄清设问的指向，再抓关键词，领悟出命题者的意图，明确本题考查的基本方向，然后再用所学知识解决问题.在排除的过程中，学生要排除明显错误、明显与题意无关的、因果关系或递进关系明显颠倒错误选项，最终留下正确答案.

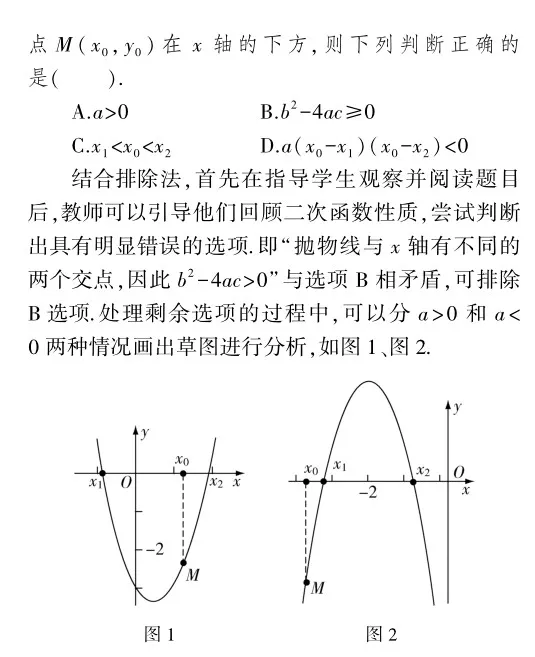
结合图示内容，学生能够获得线索，因为a的符号不能确定所以x1，x0，x2的大小就无法确定.图1中a>0且有x1

（二）特殊化法解决问题

学生在解题期间可能会遇到这样一种情况，即面对复杂问题时难以快速找到解题思路，不知如何处理问题.《新课标》强调学生需要能通过特殊结果推断一般结论.因此，教师在组织解题教学期间，可以根据数学知识的内部逻辑特点，指导学生尝试去考虑这个问题的某种特殊情况，运用特殊化法来降低问题的难度，使问题变得明朗，顺利找出解决问题的思路.

（三）整体代入法解决问题

整体代入法即把条件式看作一个整体，将其整体代入目标式，达到求解目的.用“整体代入法”求值要先确定“整体”，再将目标式进行变形与转化.整体代入也是初中数学解题中较为常见的一种方法，这种方法与直接思考方向相反，在解题的过程中，学生需要将一部分看作整体代入到其他式子中求解问题的方法，一般适合于代数式的求值题中.

二、解答题解题指导

解答题在考试中占据大部分分值，要求学生在理解数学知识、把握数学本质的基础上，灵活解决问题.为提高学生的解题效率，教师可以根据在中考中经常出现的题目类型，合理选择便捷性解法，渗透数学思想，促进学生核心素养的形成与持续发展，提高学生解答题正确率.

（一）逆向思维技巧解决问题

逆向思维，也称求异思维，它是对司空见惯的或已成定论的事物或观点反过来思考的一种思维方式.常说的“思维定式”指的是已经形成的倾向性的思维准备状态，逆向思维就是要打破这种思维定式，从事物的相反方向进行思考并处理问题，是摆脱常规思维羁绊的一种具有创造性的思维方式.在解决大题的过程中，学生需要拥有清晰的解题思路，能够灵活运用所学知识，在面对一些根据常规思维方式无法顺利解决的问题时，尝试从事物的反方向进行思考，从而寻找突破口，顺利解决问题.

比如，讲解苏科版七年级下册“认识三角形”一课期间，有这样一道问题：

如图3所示，△ABC是等边三角形，延长BC到D，延长BA到E.使得AE=BD，连接CE，DE，求证CE=DE.

从已知条件出发，学生会发现AE=BD这一条件没办法使用，无法从全等、等边对等角等方向解决问题.因此，教师需要引导学生通过逆向思维的方法，从结论反推条件，即从CE=DE着手，寻找验证此论点的条件.在教师的引导下，学生可以结合证明线段相等知识，利用全等的方式来证明.首先，可以将CE置于△BCE中，做辅助线延长CD，建立一新点F，连接EF，使得∠F=60°.在教师的引导下，学生建立辅助线，再借助AE=BD的条件，可以证明△BEC和△EDF全等来求证CE=DE.在解决此问题中，教师引导学生从结论入手，利用全等构造辅助线的方式寻找需要条件，由此利用便捷的方式解决问题.在完成讲解后，教师还可以引导学生自主探索其他解决办法，尝试将EC置于△ACE中进行证明，由此提高学生的问题解决能力.

（二）待定系数法解决问题

待定系数法是一种求未知数的方法.此种解题技巧适用于分解因式、求函数解析式、解方程、展开分式等，主要通过将多项式表示成另一种含有待定系数的恒等式，基于恒等式性质得出满足方程或方程组的系数，再通过解方程求出待定系数.在解决解答题的过程中，教师可以向学生传授待定系数法解决问题的技巧，帮助学生更好地理解数学知识的规律，把握数学本质.

比如，讲解苏科版八年级上册“用一次函数解决问题”一课期间，有这样一道问题：

某地长途汽车客运公司规定旅客可随身携带一定质量的行李，如果超过规定，则需要购买行李票，行李票费用y（元）是行李质量x（kg）的一次函数，其图像如图4所示，则旅客可免费携带的行李的质量是多少？

（三）分类讨论思想解决问题

分类讨论同样也是初中阶段数学学习的重要思想之一.在解决绝对值、等腰直角三角形、直角三角形等不确定的情况下，教师可以引导学生运用分类讨论的方式化整为零、逐个突破，从不同角度对问题进行探究，继而顺利解决当前学生存在的“不知如何着手解决问题”以及“结论不完整”的情况，有效锻炼学生逻辑思维.

比如，讲解苏科版九年级下册“二次函数与一元二次方程”一课期间，有这样一道问题：

在平面直角坐标系xOy中，已知点M，N的坐标分别为（-1，2），（2，1）若抛物线y=ax2-x+2（a0）与线段MN有两个不同的交点，则a的取值范围是多少？

在阅读题目后学生会发现，本题中并未发现a的符号，所以大部分学生不知如何解决问题.鉴于此，教师可以带领学生通过分类讨论的方式解决问题，根据已知线索，可以将本题分为两种情况进行讨论，即a>0时和a<0时.

本题求解的关键是先对抛物线开口方向进行讨论，这样通过分类讨论的方式即可轻松解决此题.在后续学习中，教师可以为学生补充类似问题，帮助他们在巩固训练中提升自我，更好地掌握解决数学问题的技巧.

结 语

综上所述，在新课标背景下教师组织初中数学解题活动期间，需要渗透数学思想，对不同题目类型采取不同的指导方法，帮助学生更好地建立数学思想，提高自身核心素养.文章中，教师分别提供了排除法、特殊化法、整体代入法、逆向思维、数形结合、待定系数法、分类讨论思想等解题技巧，以此提高数学解题教学收益，达成预期教学目标.

【参考文献】

[1]金文卫.初中数学解题中的函数思维[J].中国教育学刊，2023（3）：106.

[2]段永琴.初中数学教学中如何渗透数学思想方法[J].科学咨询（教育科研），2023（1）：186-188.

[3]李霞.基于核心素养的初中数学教学的几点思考[J].河南教育（教师教育），2022（2）：57-58.

[4]虎正伟.初中数学教学应当重视学生直觉思维的培养[J].科教导刊（中旬刊），2020（20）：152-153.

[5]范小建.初中数学解题思路与方法应用探讨[J].才智，2020（13）：193.