基于大观念的小学数学理解性学习策略研究

【摘要】小学数学教师基于学科大观念开展多样化理解性学习活动，不仅可以改变学生对数学学习的态度，快速激活他们的主观能动性，提升其自主学习的动力，还能借此培养他们结构化、深度性学习的意识，使其能够更加主动地探究知识内涵，探寻各知识点之间的内在联系，体会知识的实际作用，从而提高最终的课程学习质量.对此，为了真正达成上述目标，文章以苏教版“整数乘法”为例，阐述教师通过创建大观念、关联认知、知识实践等活动，提升深度理解教学效果的策略.

【关键词】大观念；小学数学；理解性学习

小学数学教师为了让学生更加透彻、更加深刻地理解学科概念，使他们实现有效的深度性课程学习，可以结合学科大观念创建丰富多样的理解性学习活动.在教学过程中，教师需要先科学提炼数学大观念，要明确学科概念探究的方向，再借助推导探知、深入理解、知识建构、迁移应用等活动，让学生对数学概念实现经验性理解、深度性理解、创新性理解等，从而进一步提升其课程学习的效率与效果.

一、大观念教学概述

大观念指的是在某种事实或某个概念的基础之上，对其中各要素之间关系进行高度概括，或者对核心概念进行系统性阐释和概括性的表述.在教育领域，大观念能够充分体现学科知识的核心概念以及重点内容，同时，能够客观反映学科概念的内在原理和本质规律.根据上述内容可知，大观念教学指的是教师以学科大观念或大概念为主要依据，以知识深度理解和技能实践体验为主要过程，以培养学生概念性理解能力，发展他们学科核心素养为主要目标的一种教学方法.大观念教学的本质是让学生实现对学科知识的深度性理解，旨在发展他们的逻辑思维、整合思维、发散思维等，提升其学科综合素养，从而提高最终的课程学习质量.

二、理解性学习概述

理解性学习指的是以深度理解学科概念，建构学科知识为主要目的的一种学习理论.此理论强调学习的自主性、深度性和实践性，学生需要通过主动思考、深入分析、自主实践等方式，实现对学科知识、重点概念的透彻理解，同时，建构自己的认知体系.对于理解性学习而言，深度认知学科知识的概念是最为根本的目标，这意味着教师需要明白深度理解的内涵，要有意识地引导学生对学科概念进行深层次分析与研究.对于小学数学课程而言，教师在开展理解性学习教学活动时，需要引导学生深入探究学科概念的本质与特征，同时，要让他们将其合理运用于实际问题之中，让他们在知识迁移与实践过程中更加透彻地理解概念内涵，知道学科知识的实际价值，进而提高学生深度学习的质量.

三、小学数学基于大观念开展理解性学习教学的具体措施

（一）整合学科知识，提炼课程教学大观念

在开展以大观念为基础的理解性数学认知活动之前，教师需要先整合教学材料中的知识点，引导学生根据单元内容提炼数学大观念，以此来明确学科概念深度探究的方向，为他们实现高效的理解性学习奠定良好基础.在提炼大观念过程中，数学教师需要为学生提供充足的自主思考时间，要启发他们的多维思维，使其能够在互动交流过程中初步了解各部分知识点之间的关联关系，从而提炼出更加合理、更加清晰的学科大观念.

以苏教版数学教材为例，教师可以结合三年级上册第一单元“两、三位数乘一位数”，三年级下册第一单元“两位数乘两位数”，四年级下册第三单元“三位数乘两位数”课程，创建学科大观念提炼活动.首先，教师要让学生初步了解各单元的学习内容.比如，“两、三位数乘一位数”课程包括倍的认识，一个数的几倍是多少，两、三位数乘一位数的不进位、一次进位、连续进位运算方法等知识.“两位数乘两位数”包括乘法估算，两位数乘两位数不进位、进位运算方法、两步连乘运算方法等知识点.“三位数乘两位数”课程包含三位数乘两位数的笔算方法，乘积的变化规律，乘数末尾有0的简便运算方法等知识.然后，教师引导学生综合上述内容进行交流讨论，科学提炼数学大观念.在讨论过程中，数学教师需要指导学生探讨各单元知识中的核心内容.比如，每个单元的知识点都涉及数学乘法，分别讲解了多位数与一位数相乘、多位数与多位数相乘、末尾含0、进位乘法和不进位乘法等算式的运算方法.对此，学生通过互动交流可以提炼出“数学整数乘法”这一学科大观念，同时，确定最终探知方向是理解整数乘法的含义，了解各类型整数乘法算式的运算规律和运算方法.教师创建大观念提炼活动，能够促使学生进一步明确学科概念和单元知识深度探究的方向，为之后的深度性学习奠定良好基础.

（二）丰富认知活动，提高理解性学习质量

数学教师需要围绕学科大观念，结合教学内容，开展丰富多样的深度理解性探知活动，如知识推导、深度探究、知识建构、迁移实践等，让学生在完成各种学习任务的过程中，加深对数学大观念的理解，扎实掌握相关知识技能，从而提升其课程深度学习的效果.

1.推导关联知识，激活经验性理解

数学教师可以围绕学科大观念开展知识推导学习活动，让学生结合已有经验对新知识进行推导探究，这样既可以激活他们的经验性理解，提高其推导认知的能力，又能让他们初步认识到同类型各知识点之间的关联关系，进行形成一定的关联性认知意识，提升知识探索的效率.

以苏教版三年级数学上册第一单元“两、三位数乘一位数”课程为例.在学习多位数乘一位数的整数乘法知识之前，学生已经掌握了最为基本的乘法表知识，能够快速计算一位数乘一位数的数学算式.对此，教师可以引导学生根据乘法表知识推导“倍”的概念和多位数乘法运算规律，在提升其自主认知能力和乘法运算能力的同时，加深他们对“整数乘法”大观念的理解.比如，乘法表按照从1至9的顺序进行排列.教师可以引导学生根据乘法表知识推导“倍”的概念.如5×3=15表示三个五相加，即5+5+5=15，这是将乘法转化成加法进行理解，那么，用乘法思路探究5×3=15的含义，则可以理解为三个五相加也表示五的三倍，由此推导出5×3=15的含义是5的3倍是15，学生将这一理解进行拓展引申，可以总结出“倍”的概念是指“一个数是另一个数的几倍”，用于表示一个数与另一个数的倍数关系.

除此之外，教师还可以指导学生根据乘法表推导两位数乘一位数和三位数乘一位数的算法.比如，学生结合“倍”的概念能够理解22×3算式表示22的3倍是多少.针对此乘法算式，教师先让学生回忆乘法表中2和3的算法，即2×3=6.然后，教师教授学生竖式算法的计算思路，鼓励他们结合已有经验尝试推导运算，如22×3乘法算式，先用乘数中的个位数与被乘数相乘，再用乘数中的十位数与被乘数相乘，因为此算式不进位，所以分别相乘后所得的66即为最终结果.数学教师开展关联知识推导探知活动，既可以启发学生的联想思维、推理思维，又能帮助他们进一步理解整数乘法的概念，提升其经验性理解学科大观念的能力.

2.交流知识内涵，达成深度性理解

数学教师为了让学生对“整数乘法”这一大观念产生更深层次的理解，可以围绕单元知识，结合生活元素，开展深度交流学习活动.在此项活动中，教师可以借助常见事物或日常现象引导学生对乘法算式的含义进行深入研究，使其在交流探讨过程中进一步理解乘数、被乘数、积、倍的概念，明白乘法算式的本质内涵，从而真正达成深度性理解认知，提高整数乘法理解性学习的质量.

以苏教版数学三年级下册第一单元“两位数乘两位数”课程为例.此单元知识建立在多位数乘一位数的乘法知识基础之上，包括两位数乘两位数的估算、两位数乘两位数不进位算法和进位算法、两位数乘整十数的算法、两步连乘算法知识点.在“整数乘法”大观念深度理解课程中，教师可以设计简单的多位数相乘算式，引导学生结合现实生活元素进行算式含义理解.例如，教师先用多媒体课件展示用鲜花表示的乘法算式图片，如一个演出场景中有24束鲜花，每束鲜花中有12支玫瑰花，问一共有多少支玫瑰花，此道题的算式为12×24.对此，教师需要让学生深入研究12×24乘法算式的含义.在深入理解过程中，教师可以让学生结合画面内容进行拓展思考，比如，24束玫瑰花，每束有12支，那么，两束玫瑰花共有多少朵？可列式为12+12，即24支，而此加法算式也可看作是12×2乘法算式.运用此种思路进行延伸推导，既可以理解24束玫瑰花的数量是每束12支相加24次，即12的24倍，由此，学生能够推理出12×24算式的含义，如12支玫瑰花的24倍是多少.之后，教师再用竖式指导学生计算两位数乘两位数进位乘法算式，让他们掌握正确的笔算方法.学生通过参与此类活动，能够进一步提高深度理解数学大观念的能力，进而加深对乘法算式含义的理解.

3.构建知识体系，实现结构性理解

在以大观念为基础的数学教学课程中，教师为了让学生对“整数乘法”知识形成一个整体性认知，让他们建立更加完整的知识结构，可以创建理论与技能知识体系建构活动.这样既可以培养学生结构性理解能力，又能让他们逐渐形成较强的系统化学习意识，使其能够从宏观视角出发对“整数乘法”大观念进行深入分析，在探究各概念、各理论内在关联关系的同时，构建出逻辑清晰、内容完整的整数乘法知识体系.

以苏教版四年级数学下册第三单元“三位数乘两位数”课程为例.教师在教授学生三位数乘两位数不进位乘法和进位乘法的算法、乘数末尾有0的多位数乘法算法、积的变化规律之后，可以综合学生已掌握的所有整数乘法知识开展知识体系建构活动，以此来加深他们对数学大观念的结构性理解.首先，教师要让学生汇总所有学过的整数乘法知识，如乘法概念、倍的概念、个位数乘法算法、多位数乘法算法、乘法估算、积的变化规律等.然后，教师让学生进行互动讨论，对上述知识点进行合理分类.比如，所有理论性乘法知识为一类，所有实践性算法知识为一类；或者概念性知识为一类，个位数乘法为一类，多位数乘一位数为一类，多位数乘多位数为一类.之后，教师可以引导学生按照不同类别补充详细信息，构建大观念知识体系（如图1）.

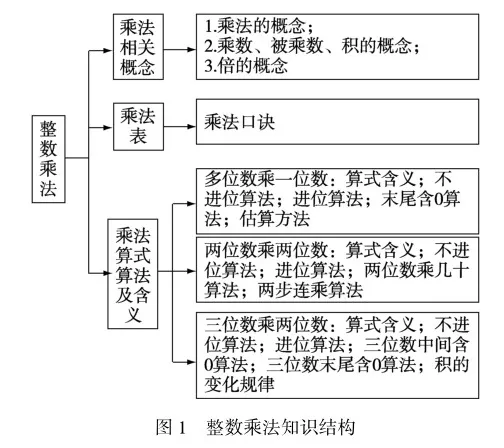
教师通过创设数学知识体系建构活动，能够有效培养学生结构化理解“整数乘法”大观念的意识，同时，提高他们的逻辑思维能力、知识梳理能力和知识整合能力，进而提升其系统化理解性学习的质量.

4.迁移应用知识，激活创造性理解

在学科大观念教育指导下，教师不仅要让学生更加透彻地理解数学大观念的含义，还要培养他们结合大观念，运用相关知识解决数学问题的能力.对此，教师可以利用现实元素，创建知识迁移实践活动，让学生灵活运用整数乘法知识，采用多种方法解决与之相关的实际问题，使其更加真切地体会到数学乘法的现实意义.另外，教师可以借此培养学生的创造性理解能力，提高他们知识实践运用的水平.

以苏教版数学三年级下册第一单元“两位数乘两位数”课程为例.针对此单元两位数与两位数不进位乘法、两位数与两位数进位乘法、两步连乘乘法知识，数学教师可以结合现实案例开展创造性问题解决活动，让学生通过解答实际问题，提高他们应用“整数乘法”大观念及其相关算法知识解决现实问题的能力，同时，提升其创造性理解数学大观念的水平.例如，教师可以出示如下问题：一家体育商店的跳绳按“袋”售卖，一袋有5个，每个8元，学校购买6袋，问一共需要多少钱？购买了多少个跳绳？针对此题，教师要鼓励学生采用多种思路进行计算.比如，学生通过对“整数乘法”大观念的理解，能够列出如下几种算法：（1）先算5×8得出一袋40元，再算40×6得出共花费240元，再算5×6得出30个跳绳；（2）先算5×6得出30个跳绳，再算30×8得出240元；（3）直接计算5×8×6得出240元，再算5×6=30跳绳数量.学生通过多角度思维问题，多方法解答问题，既可以提高知识灵活运用的能力，又能加深对整数乘法的理解，从而提升课程深度学习的效果.

结 语

综上所述，小学数学教师若想进一步增强“整数乘法”教学的深度性、整体性和有效性，可以基于大观念开展多样化理解性学习活动，让学生通过对乘法知识进行关联性推导、深度性理解、系统化梳理、创造性运用，加深对整数乘法概念的理解，提高运用乘法知识解决相关问题的能力，从而提高课程学习的质量.

【参考文献】

[1]崔洪喜.大观念视角下的小学数学单元整体教学[J].天津教育，2022（23）：21-23.

[2]蒋敏，张月明.“为理解而教”：让学生走向深度学习[J].知识窗（教师版），2022（6）：69-71.

[3]张媛媛.小学数学深度学习：从概念理解到课堂实践[J].新课程教学（电子版），2022（11）：89-91.

[4]黄家硕，李纪飞.深度教学视角下的小学数学理解性教学策略[J].数学学习与研究，2021（34）：140-142.

[5]吴存明.为“理解”而教：以小学数学为例[J].教育研究与评论，2021（4）：69-73.