“数形结合思想”在小学数学教学中的应用

【摘要】“数形结合思想”的应用，旨在通过将“数”与“形”两类数学要素进行转化或融合，简化数学知识的理解难度，活跃学生思维，提高他们解决数学问题的能力.文章分析了“数形结合思想”的含义，探究了应用“数形结合思想”的理论基础，研究了在小学数学课程中应用此种思想的要点，从知识探索和运用两方面视角，阐述开展“数形结合”类探知活动，设计以数解形、借形解数等问题，提高数学教学质量的策略，旨在为教师合理应用“数形结合思想”提供思路.

【关键词】数形结合；小学数学；数学思想

《义务教育数学课程标准（2022年版）》指出，教师应当开展能够促进学生的发展的教学活动，要让他们经历观察、思考、分析、推理、计算等数学认知过程，使其真正体会和运用数学的思想与方法，从中积累更多有价值的数学活动经验，进而提升数学学习能力和学科素养.对此，教师可以在小学数学课程中，引入“数形结合思想”，应用此种思想，指导学生进行理论探究和技能实践，让他们掌握以数解形、以形解数的方法，使其在数形互译过程中，深度理解数学知识，提高解决数学问题的效率与能力.

一、“数形结合思想”概述

“数形结合思想”指的是根据数与形之间的关系，将抽象数量与具象图像进行关联对应，通过数与形之间相互辅助、相互转化、相互指引的方法，理解数学知识、解决数学问题的一种数学思想.“数形结合思想”中“数”与“形”之间是相互转化、相互辅助的，可以用“数”的形式表现“形”，体现事物的具体数量或增减变化，也可以用“形”的方式探索“数”，直观呈现数量之间的关系等.

“数形结合思想”的应用不仅能够将抽象的数学概念、数量关系、数学规律等以直观、形象的方式呈现出来，使学生更加深刻地理解数学知识的本质，还能有效活跃他们的思维，使其能够通过数形转化、数形互译等方式，快速解决数学问题，进而提升知识迁移运用的水平.

二、“数形结合思想”的理论基础

（一）脑科学理论

脑科学理论由美国神经生物学家斯佩里提出，该理论强调人类大脑由左、右两个部分构成，而左脑和右脑有着不同的思维方式，左脑更具有分析性、逻辑性特点，善于研究概念性、理论性问题，右脑则具有无序性、跳跃性特点，善于处理一些感知类、视觉类问题.这一理论指出了左、右脑各自具备的特征和优势，说明了对人类的左右脑进行共同开发，能够使其产生对世界实现感性与理性交织的认知.在“数形结合思想”中，“数”更倾向于左脑认知，“形”则倾向于右脑认知.对此，教师可以根据脑科学理论，将“数”与“形”进行合理融合，引导学生同时运用左、右脑认知数学知识，解决数学问题.

（二）认知结构理论

认知结构理论由美国认知心理学家布鲁纳提出，该理论认为人类对世界的认知是在原有认知结构的基础上，对听到的、看到的新信息进行关联和重组，从而实现对外界认知的不断建构.另外，在认知建构过程中，人们并不是简单的组合或罗列信息，而是要根据各信息之间的逻辑关系进行科学联结.对此，根据这一理论，教师在“数形结合思想”应用过程中，需要引导学生发现“数”与“形”之间的内在联系，不能随意选择数学图形或模型与数量关系相连，这样才能使“数”与“形”之间实现有效转化或融合.

三、“数形结合思想”的应用要点

（一）注重数形之间的对等性

教师在数学课程中应用“数形结合思想”时，需要遵循数与形之间的对等性原则，要让学生深入了解数字、数量、图形、图像等要素之间的关系，使其能够在特定的情境或条件下，对数与形进行合理转换或相互替代，这样才能用“形”解决相关的“数”的问题，或者用“数”表示相应的“形”的问题.

（二）突出数形之间的互换性

另外，教师引导学生运用“数形结合思想”探究知识或解决问题时，需要遵循数形之间的互换性原则，要引导学生用数字、数量关系等数学语言描述图形，揭示图形特征等，用图形、图像、模型等形象化方式，表示抽象的数学规律、数量关系等，使其通过对数与形进行合理转化，加深对数学知识的认识，同时，掌握“数形结合思想”的运用方法.

四、“数形结合思想”在小学数学中的应用措施

（一）巧用“数形结合思想”，探究数学知识

在数学复杂概念、抽象规律教学过程中，教师为了降低知识的理解难度，提高学生的学习效果，可以应用“数形结合思想”开展教学活动，引导学生运用图形解析算理，用数量表示图形知识等，以此来加深他们对数学知识的理解.

1.借助图形，揭示数学算理

小学数学教材中的知识通常按照从易到难的递进顺序编排，学生随着学习内容的不断进阶，要掌握的知识也更加抽象，更加复杂.比如，在第二阶段的数学学习中，学生需要从简单的整数运算知识过渡到分数、小数运算知识.对此，教师为了让学生能够更加快速地掌握较为抽象的数学算理，使其能够真正理解分数运算或小数运算的内在逻辑，提升他们的运算能力，可以应用“数形结合思想”，借助直观图形，开展算理形象化探究活动.

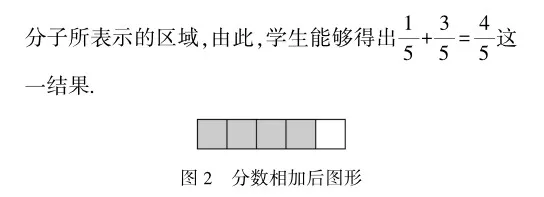
针对上图内容，教师还需要引导学生进行深入探究，使其通过分析图形的移动与组合，理解同分母分数相加的算理，即相同分母的分数相加，其分母不变，只相加分子.教师引导学生将算式转化成图形，能够使其更加直观地理解数学算理，进而提高数学运算能力.

2.以数助形，揭示图形知识

图形本身具有直观、形象的特征，对于学生来说，他们也更容易掌握图形的特点、图形计算等知识，但是，他们可能会在理解和描述图形的性质、图形的规律等方面遇到困难.对此，教师可以引导学生运用“数形结合思想”，借助数字或数量关系等“数”的表示方法，对稍有难度的图形知识进行分析与研究，使其能够运用理性思维、数学语言，客观描述与图形相关的理论、性质、规律等，进而深化学生对图形知识的理解，使其进一步体会“数形结合思想”.

以人教版小学数学四年级下册第七单元“图形的运动（二）”教学为例.针对此单元“图形的平移”知识，教师可以借助“数”的语言，引导学生探究平移的性质和规律.例如，教师先在多媒体课件中展示一幅格子图，图中有一个用三角形和不规则图形组合而成的“火箭”图形，每个小方格边长为1cm.然后，教师引导学生将该图形进行分割和移动，通过移动使其重新组合成一个长方形，就可以根据方格计算长方形的面积了.对此，学生需要将图形分割成一个三角形和一个不规则图形（如图3），而后将三角形向左边平移一定的格数，将不规则图形补充完整，从而得到长方形.

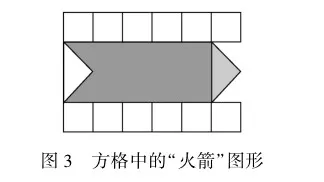
之后，教师让学生对三角形的移动过程进行描述，比如，三角形向左平行移动5个方格；三角形向左平移5厘米等.学生用数学语言和数字对平移方向、平移距离进行描述，能够理性呈现图形的平移规律和平移性质，从而深刻理解图形的平移知识.

（二）运用“数形结合思想”，解决数学问题

教师为了提高学生知识实践的能力，可以运用“数形结合思想”，创建丰富多样的解题活动，让他们通过解答以数解形问题、借形解数问题、数形互译问题等，增强思维的灵活性、敏捷性、逻辑性等，同时，提高解决数学问题的效率.

1.设计以数解形问题

教师为进一步强化学生的“数形结合思想”，使其能够更加快速地厘清数学问题的解决思路，更加精准地用数学语言阐述问题的结论，可以围绕“以数解形”设计数学问题.针对此类问题，教师需要引导学生自觉探究与题中图形或图像相关的数字或数量关系，让他们对“形”赋予相应的“数”的含义，用“数”客观描述或表示“形”，从而快速探索出问题的答案，提高以数解形的能力.

以人教版小学数学五年级上册第二单元“位置”教学为例.此单f88098f3e64eaf5d536e4a011c7071bd元包括行、列、数对的概念，以及用一组数对表示一个位置等知识.对此，教师可以围绕“数对”知识设计以数解形问题，让学生通过自行解答问题，更加扎实地掌握用数对表示位置的方法.例如，教师先将班级座位以行列示意图的方式呈现在大屏幕上，引导学生先理解“行”和“列”的概念.然后，教师指导学生掌握用数“行”和数“列”的方式确定某个人的位置，以及用数对方式表示示意图中的对应位置的方法.之后，教师再设计一道问答题，让学生运用所学方法自行确定某个人在示意图中的位置.例如，教师让学生用数对方式表示班长在班级中的位置.对此，学生需要将班级座位与示意图相关联，确定行与列的方向和数量，而后找到班长座位在示意图中的对应位置，同时，确定行数和列数，找到行与列的交叉点.通过以上讲解，学生能够顺利用（列，行）数对方式，表示班长所在的位置.学生通过解答上述问题，能够将图像信息科学转化成数字信息，形成较强地应用“数形结合思想”解题意识，同时提高解题的效率.

2.设计数形互译问题

教师除了设计“数”与“形”单方面转化的问题之外，还可以设计两者互译类问题，让学生先根据已知的数量关系、数字信息等，将其转化成相应的图形或数据模型，把复杂的数学问题进行直观化呈现，然后对直观图像进行深入解析，找到相关的数学规律，厘清数学解题的思路，探索出更加便捷的解题方法.之后，学生根据已有经验对图形进行测量和计算，或者对数据模型进行分析和推测，而后对其进行一次转化，用数学语言表示问题的结论.教师设计数形互译问题，既可以使学生更加深入地体会“数形结合思想”，又能借此提高他们灵活、快速解决数学问题的能力.

以人教版小学数学六年级上册第八单元“数学广角──数与形”教学为例.此单元要求学生掌握运用“数形结合思想”，通过相互印证解决数学问题的方法，知道与“形”有关的问题中包含着“数”的规律，而“数”的问题可以用“形”的方式辅助解决.另外，学生需要感受以形解数的直观性和简洁性，体会以数助形的逻辑性、抽象性.对此，针对上述课程目标，教师可以仿照单元案例，围绕某个知识点设计与之相似的数形互译问题.例如，教师围绕“可能性”知识，设计如下问题：在四个完全相同的乒乓球上分别标注2，3，4，5四个数字，然后将它们放入一个不透明的箱子中，第一次任意抽出一个乒乓球，不再放回，第二次再任意抽出一个乒乓球，问两次抽出乒乓球的数字之和是7的可能性为多少？对于这个问题，学生可以根据已知条件，绘制数学模型（如图4），清晰表示两次分别抽到某个数字的具体情况.

结 语

综上所述，对于小学数学教学而言，教师若想进一步增强课程教学的灵活性、探究性，快速发展学生的思维能力，提高其知识理解和知识应用的水平，可以将“数形结合思想”融入教学过程之中，让学生在数和形灵活转化的同时，加深对抽象知识的理解，形成较强的解决数学问题的能力.

【参考文献】

[1]陈丽芳.数形结合思想在小学数学教学中的运用研究[J].数学学习与研究，2023（35）：87-89.

[2]张慧贞.小学数学教学中培养学生数形结合思想的策略研究[J].教师，2023（35）：27-29.

[3]夏晓明.小学数学教学中渗透数形结合思想的策略[J].学苑教育，2023（35）：31-33.

[4]陈鹭.数形结合思想在小学数学课堂教学中的应用[J].新课程导学，2023（34）：39-42.

[5]林悦.数形结合思想在小学数学教学中的实践[J].小学生（上旬刊），2023（12）：91-93.