基于Bloom Filter本地差分隐私的基数估计

摘 要：计算机技术和通信技术的共同发展，使得数据呈现指数大爆炸式的增长。数据中蕴含的巨大价值是有目共睹的。但是对数据集的肆意收集与分析，使用户的隐私数据处在被泄露的风险中。为保护用户的敏感数据的同时实现对基数查询的有效响应，提出一种基于差分隐私的隐私保护算法BFRRCE（Bloom Filter Random Response for Cardinality Estimation）。首先对用户的数据利用Bloom Filter数据结构进行数据预处理，然后利用本地差分隐私的扰动算法对数据进行扰动，达到保护用户敏感数据的目的。

关键词：隐私保护；本地化差分隐私；Bloom Filter；基数；随机响应

中图分类号：TP309 文献标志码：A 文章编号：2095-2945（2024）28-0035-04

Abstract： The joint development of computer technology and communication technology has led to exponential explosive growth in data. The huge value contained in the data is obvious to all. However， the wanton collection and analysis of data sets puts users 'private data at risk of being leaked. In order to protect users 'sensitive data while achieving effective responses to cardinality queries， this paper proposes a privacy protection algorithm， BFRRCE（Bloom Filter Random Response for Cardinality Estimation）， based on differential privacy. First， the user's data is preprocessed using the Bloom Filter data structure， and then the data is disturbed using a local differential privacy perturbation algorithm to achieve the purpose of protecting the user's sensitive data.

Keywords： privacy protection; localized differential privacy; Bloom Filter; cardinality; random response

随着信息技术和网络技术的迅速发展，数据的类型和数据量在不断地增长。大数据驱动的管理与决策发展核心是不同行业领域之间的数据资源开放，目前大数据贯穿七大行业：商务、金融、医疗健康、教育、交通、电力以及石油业天然气[1]。但数据的开放和共享必然会带来隐私数据保护的问题。

保护隐私的技术有很多种，如匿名化技术[2]、加密技术[3]等，但是它们都是基于攻击者知识背景的改变而进行改进，且无法提供可量化的隐私保证。基于上述原因，差分隐私[4-5]被Cynthia Dwork提出。

基数是一个十分重要的数据集的数字特征。近年来对于数据集进行估计的方法大致可以分为3大类：第一类是基于概要的方法得到的，文献[6]是利用概率统计的方法做的，本文并未涉及隐私保护，但蕴含着PCSA sketch的核心思想，其思想在文献[7]和文献[8]中都有体现，文献[7]只是针对2个数据集，即2个用户的基数估计，且其扰动概率的设置使得其基数查询的精度并不高。文献[8]提出了2种方法，一个是确定性合并同样也是针对2个用户的数据进行保护的，所以当面对多用户时是不可行的。第二种方法是随机性合并，它可以处理多用户的基数估计，但是在用户数较多时，算法所需的扰动概率矩阵在运算时是会经常溢出的。第二类是基于采样的方法。涉及到的文献[9]是基于采样的方法，因为只利用了数据集的部分信息，所以基数估计的误差相对来说还是很大的，且文献没有涉及到隐私保护。第三类是基于学习型基数估计的方法。涉及到的文献[10]是通过无监督学习学到一个与负载无关的模型来近似极大似然估计，且文献中同样未涉及隐私保护。为了弥补上述问题，提出了一个基于Bloom Filter本地差分隐私的基数估计算法。

1 相关知识背景

1.1 基数查询

基数：在数学上被用来描述集合的大小，是指一个集合中不重复的元素的数量。例如数据集A中虽然有{a，a，b，b，c}，但是它的基数是3，因为数据集A中只有a、b以及c 3类数据。

对数据集进行基数查询有十分重要的意义。以广告商投放广告费为例，第一次广告商在APP1、APP2和APP3 3个平台上投放广告，投放的广告费分别为2万元、3万元以及5万元。但是经过统计发现在3个平台观看广告的用户的基数分别为50万人、20万人和10万人，基数和为52万人。观察可以发现广告费在APP2和APP3投放得到的结果是不如意的，因此我们可以通过上述结果去调整广告费的投放方案。因此进行基数估计是有现实意义的。

1.2 本地化差分隐私模型

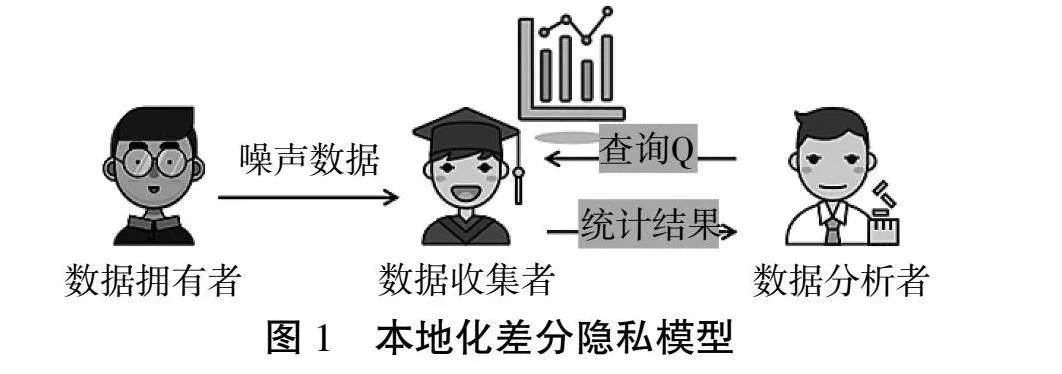
与传统的隐私保护技术相比，差分隐私保护技术[4]假设攻击者拥有最强的知识背景。差分隐私保护技术常用的模型有中心化差分隐私保护模型[5]和本地化差分隐私保护模型[11]。本文使用的是本地化差分隐私保护模型。本地化差分隐私模型中包含3个关键的角色：数据拥有者（用户）、数据收集者以及数据分析者。本地化差分隐私模型下假设拥有者对数据收集者是不信任的，所以数据拥有者自己将自己的数据通过本地化差分隐私的扰动机制将自己的数据加噪后得到的噪声数据发送给数据收集者。数据收集者对所有数据拥有者发送的数据进行统计分析，然后将统计结果发送给数据分析者，以此响应查询数据分析者的查询请求，如图1所示。

定义1（本地化差分隐私）。对于任意2个不同的值？淄和？淄′，在隐私算法M的作用下得到相同输出的概率满足下列不等式时，隐私算法M满足ε-本地化差分隐私。

， （1） 式中：P表示概率；y表示隐私算法作用在值v之后得出的噪声值；e表示自然对数的底数值，为2.718 28；ε代表隐私预算，而隐私预算越小，则意味着隐私保护程度越高[11]。

1.3 随机响应机制

本文使用的隐私算法为RR[12]。RR算法是Warner在1965年提出的，是一种十分经典的隐私保护算法。它是针对二类敏感问题（答案只有“yes”或者“no”）提出的隐私保护算法，核心思想是利用用户对敏感问题回答的不确定性来保护用户的敏感数据。一个经典的例子，要调查n个用户中患有糖尿病的占比，显然这个问题对于用户来说是敏感的，答案只有“yes”或者“no”。用户在回答问题前抛出硬币，正面朝上的概率为p，用户真实回答问题；反面朝上的概率为1-p，用户非真实回答问题。当然为了使统计信息是可用的通常p是大于0.5的。通过这种不确定性RR隐私算法保护了用户的敏感信息。数据收集者将收集到用户的回答，经统计发现回答yes的有n1个，假设实际的患有糖尿病的有nyes个。

根据概率论相关知识可知

， （2）

由极大似然估计可知

根据定义1的公式（1）计算，要想RR机制满足本地化差分隐私p要满足条件

所以符合本地化差分隐私的RR隐私算法可以用以下公式表示

。 （5）

1.4 Bloom Filter结构

本文使用的存储结构为Bloom Filter是由0/1组成的向量，可以用来检测一个元素是不是存在于集合中，因此也可用于去重。它是利用哈希函数，将一个元素映射到一个长度为L的数组上的一个bit上，当这位是1时，那么这个元素在集合中。反之，则不在集合内。这个方法的缺点是当检测的元素很多的时候可能有冲突，解决的办法就是使用k个哈希函数对应k个bit，如果所有的bit 都是1的话，那么元素在集合内，如果有0的话，元素则不在集合内。

2 BFRRCE算法

2.1 BFRRCE算法的伪代码

输入：n个用户的数据，长度为L的，有l个哈希函数的Bloom Filter B。隐私预算ε。

输出：满足本地化差分隐私的基数查询ce。

数据分析者初始化好B之后将其发送给所有的数据拥有者。

数据拥有者端：

1）For每一个数据拥有者do：

2）将自己的值？淄i映射到B中记作Bi。

3）对Bi的每一位独立的使用RR扰动机制得到。

4）将发送给数据收集者。

数据收集者端：

5）将收集到的所有数据拥有者发送的报告按列相加并校正来重构Bloom Filter B″。

6）对范围内的所有数据逐个检验是否在数据集中，在ce=ce+1。

7）Return ce。

2.2 BFRRCE算法的隐私性和可用性证明

定理1即BFRRCE满足ε-本地化差分隐私。

因为Bloom Filter有l个哈希函数。所以任意2个用户的值最多有2l个bit位不同，由定义1可知BFRRCE要想满足ε-本地化差分隐私，需要证明BFRRCE机制满足下列不等式

所以只需要对Bloom Filter的每一位按位扰动，扰动概率如下列公式所示时，BFRRCE满足ε-本地化差分隐私。

式中：Pr表示事件发生的概率，j表示构造出的Bloom Filter矩阵B这个数据结构的第j列。

定理2即BFRRCE算法得到的估计是无偏的，即E（（ΣBi[j]））=C（ΣBi[j]），E为期望。

C（ΣBi[j]）表示不经过隐私算法保护，数据收集者将所有Bloom Filter按列求和后得到的重构的Bloom Filter的第i个bit位的真实计数。（ΣBi[j]）表示数据收集者将所有的噪声Bloom Filter按列求和后得到的重构的Bloom Filter得到的第i个bit位的估计计数。

证明：假设B″[j]表示数据收集者对所有数据拥有者发来的Bloom Filter的按列求和后得到的重构Bloom Filter中第i个bit位观测值。

。（8）

求解式（8）可得

所以（ΣBi[j]）的期望值为

由公式（8）可得

3 应用实验

3.1 实验环境和数据

硬件环境为8 GB内存、4核Intel CPU（4 GHz），Windows 10操作系统上运行。算法是采用Python语言实现的，并使用MATLAB软件绘制数据结果的图。

论文是在合成数据集和比特币交易信息的真实数据集上做的。合成数据集1的基数ce为122，数据量为2 000。合成数据集2的真实基数ce为122，数据量大小为10 000。

3.2 实验方法

本文采用的是用平均相对误差绝对值对文中提出的算法进行度量的。

式中：ce表示数据集的真实基数值，e表示对数据集基数值ce的估计值，所以AARE越小说明算法的精度就越高，越大说明算法的精度就越低。

3.3 实验结果

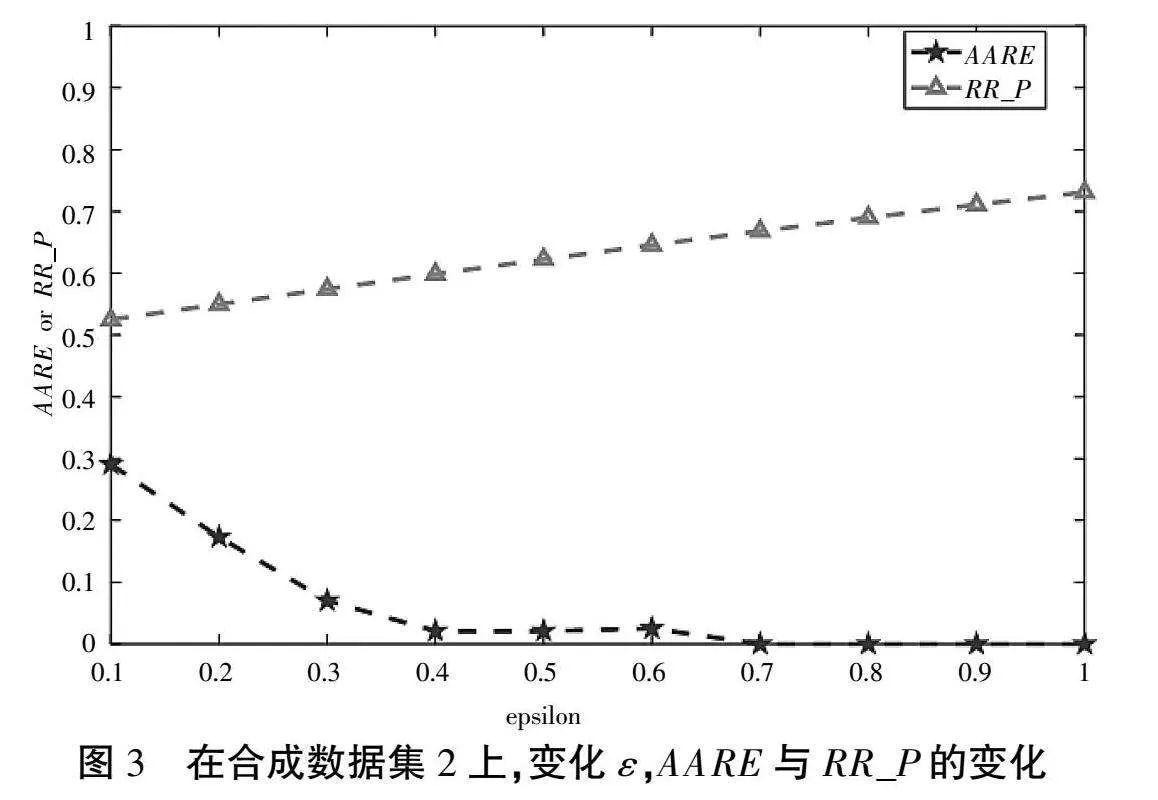
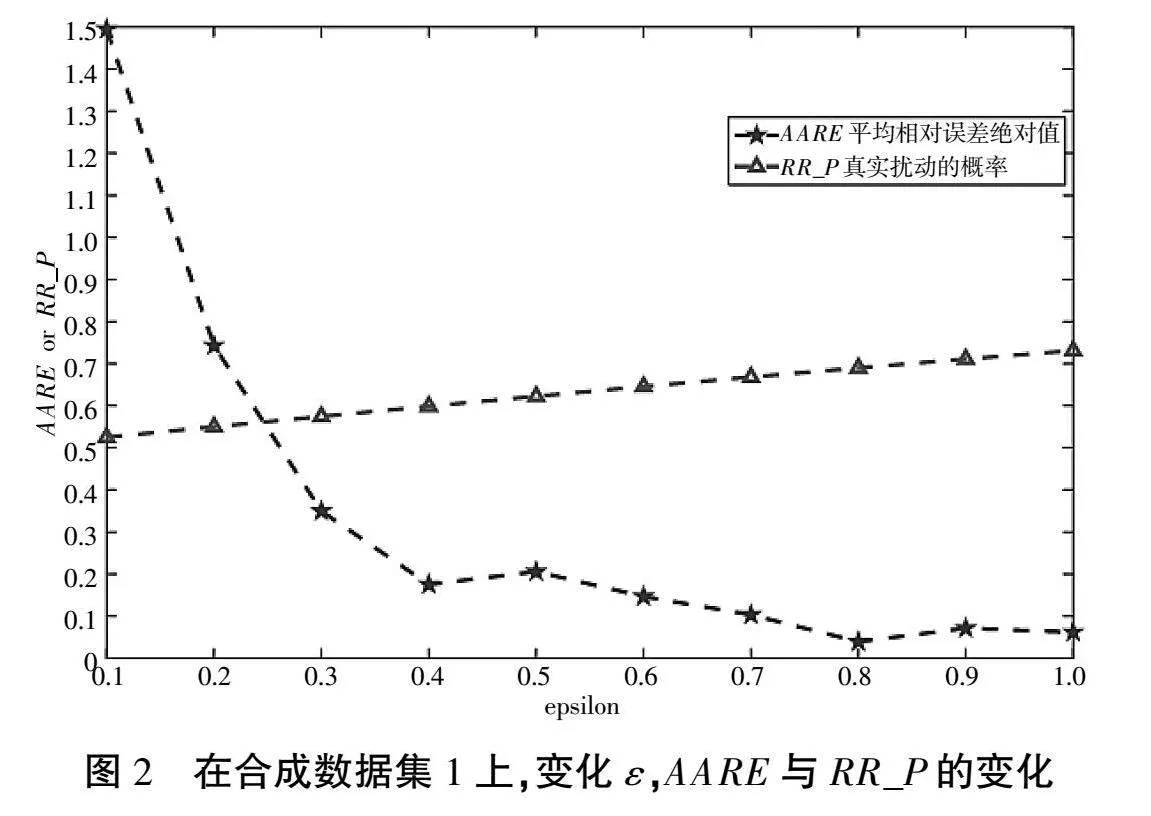
观察图2和图3可以发现，随着ε的增大，真实扰动的概率RR_P也增大，基数估计的精度就越高，平均相对误差总体呈递减的趋势。

当ε小于等于0.3时，平均相对误差是相对较高的，其原因是当ε小于等于0.3时真实扰动的概率RR_P接近于0.5，可以理解为被问二类敏感问题的受访者随机说了一个答案，没有提供任何有用的信息。

当ε大于等于0.4时，真实扰动的概率RR_P是近似大于等于0.6的，受访者回答的信息是更可用的，因此平均相对误差绝对值是较小的，基数估计的精度是较高的。

4 结论

本文通过分析当前数据收集与分析面临的问题提出了BLRRCE算法在保护用户敏感数据的同时，实现了对数据集的基数查询。为差分隐私技术的推广以及服务商为用户提供更人性化服务起到了正向的影响。

参考文献：

[1] 张啸剑.差分隐私理论与实践[M].北京：经济管理出版社，2021.

[2] LATANYA S. k-anonymity： a model for protecting privacy[J]. International Journal of Uncertainty， Fuzziness and Knowledge-Based Systems，2002，Volume 10Issue 5：557-570.

[3] STEHLE D， STEINFELD R. Faster fally homomorphic encryption[C]// Proc of the 16th Int Conf on the Theory and Application of Cryptology and Information Security. Berlin：springer， 2010：377-394.

[4] CYNTHIA D， AARON R. The Algorithmic Foundations of Differential Privacy[J]. Found. Trends Theor. Comput. Sci. 2014，9（3-4）： 211-407.

[5] DWORK C. Differential Privacy[C]// Proc of the 33rd Int Colloquium on Automata， Languages and Programming， 2006：1-12.

[6] FLAJOLET P， MARTIN G. N. Probabilistic counting algorithms for data base applications[J]. Journal of Computer and System Sciences，1985，31（2）：182-209.

[7] RASMUS P， NINA M S. Efficient Differentially Private F0Linear Sketching[C]//arXiv：2001.11932 [cs. DS]， Jan 2020.

[8] GRAHAM C， JONATHAN H. Sketch-Flip-Merge： Mergeable Sketches for Private Distinct Counting[C]// Proceedings of the 40th International Conference on Machine Learning Proceedings of Machine Learning Research 2023：12846-12865.

[9] LI J J， WEI Z W， DING B L， et al. Sampling-based Estimation of the Number of Distinct Values in Distributed Environment[C]//In Proceedings of the 28th ACM SIGKDD Conference on Knowledge Discovery and Data Mining（KDD '22）.2022：893-903.

[10] WU R Z， DING B L， CHU X， et al. Learning to be a statistician： learned estimator for number of distinct values[C]//Proceedings of the VLDB Endowment，2022，15（2）：272-284.

[11] DWORK C. Differential Privacy：A Survey of Results[C]// Proc of the 5th Int Conf on Theory and Applications of Models of Computation， 2008：1-19.

[12] WARNER S L. Randomized response： A survey technique for eliminating evasive answer bias[J]. Journal of the American Statistical Association， 1965， 60（309）： 63-69.